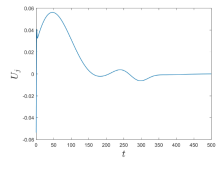
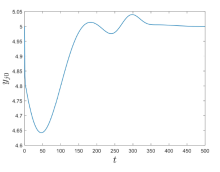
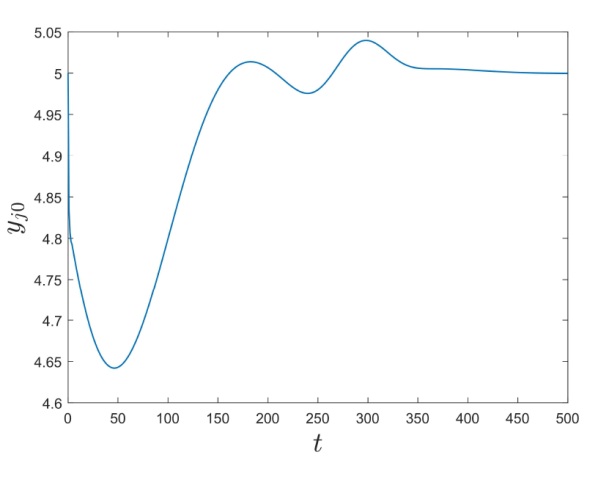
Acta mathematica scientia,Series A ›› 2023, Vol. 43 ›› Issue (6): 1803-1813.
Previous Articles Next Articles
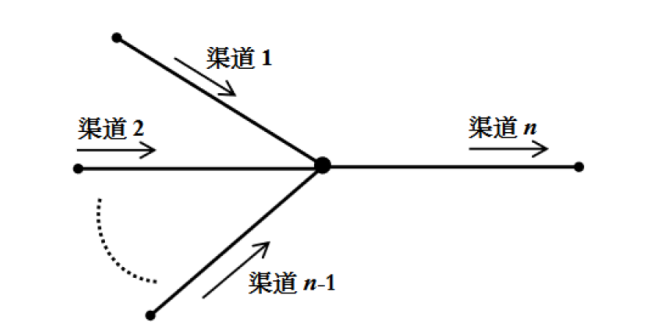
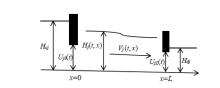
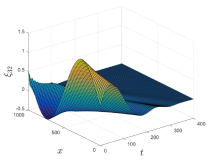
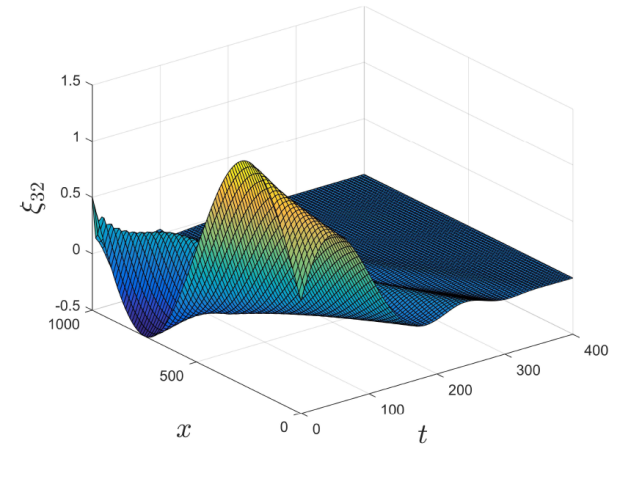
The PDP Feedback Control and Exponential Stabilization of a Star-Shaped Open Channels Network System
- School of Science, North University of China, Taiyuan 030051
-
Received:2022-11-03Revised:2023-08-16Online:2023-12-26Published:2023-11-16 -
Supported by:Fundamental Research Program of Shanxi Province(20210302123046)
CLC Number:
- O231.4
Cite this article
Pang Yuting, Zhao Dongxia. The PDP Feedback Control and Exponential Stabilization of a Star-Shaped Open Channels Network System[J].Acta mathematica scientia,Series A, 2023, 43(6): 1803-1813.
share this article
| [1] |
Litrico X, Fromion V, Baume J P, et al. Experimental validation of a methodology to control irrigation canals based on Saint-Venant equations. Control Engineering Practice, 2005, 13(11): 1425-1437
doi: 10.1016/j.conengprac.2004.12.010 |
| [2] |
Santos V D, Prieur C. Boundary control of open channels with numerical and experimental validations. IEEE Transactions on Control Systems Technology, 2008, 16(6): 1252-1264
doi: 10.1109/TCST.2008.919418 |
| [3] |
Bastin G, Coron J M, d'Andrea-Novel B. On Lyapunov stability of linearised Saint-Venant equations for a sloping channel. Networks and Heterogeneous Media, 2009, 4(2): 177-187
doi: 10.3934/nhm.2009.4.177 |
| [4] |
Halleux J D, Prieur C, Coron J M, et al. Boundary feedback control in networks of open channels. Automatica, 2003, 39(8): 1365-1376
doi: 10.1016/S0005-1098(03)00109-2 |
| [5] | Halleux J D, Bastin G, d'Andréa-Novel B, et al. A Lyapunov approach for the control of multi reach channels modelled by Saint-Venant equations. IFAC Nonlinear Control Systems, 2001, 34(6): 1429-1434 |
| [6] |
Trinh N T, Andrieu V, Xu C Z. Boundary PI controllers for a star-shaped network of    |
| [7] |
Trinh N T, Andrieu V, Xu C Z. Output regulation for a cascaded network of    doi: 10.1016/j.automatica.2018.01.010 |
| [8] |
Zhao D X, Fan D X, Guo Y P. The spectral analysis and exponential stability of a 1-d    |
| [9] |
Hayat A, Shang P P. A quadratic Lyapunov function for Saint-Venant equations with arbitrary friction and space-varying slope. Automatica, 2019, 100: 52-60
doi: 10.1016/j.automatica.2018.10.035 |
| [10] | Bastin G, Coron J M. Stability and Boundary Stabilization of 1-D Hyperbolic Systems. Switzerland: Birkhäuser, 2016 |
| [11] |
Tallman G, Smith O. Analog study of dead-beat posicast control. Ire Transactions on Automatic Control, 2003, 4(1): 14-21
doi: 10.1109/TAC.1958.1104844 |
| [12] | 蔡国平, 陈龙祥. 时滞反馈控制的若干问题. 力学进展, 2013, 43(1): 21-28 |
| Cai G P, Chen L X. Some problems of delayed feedback control. Advances in Mechanics, 2013, 43(1): 21-28 | |
| [13] |
Liu B, Hu H Y. Stabilization of linear undamped systems via position and delayed position feedbacks. Journal of Sound and Vibration, 2008, 312(3): 509-525
doi: 10.1016/j.jsv.2007.11.001 |
| [14] |
Wang J M, Lv X W, Zhao D X. Exponential stability and spectral analysis of the pendulum system under position and delayed position feedbacks. International Journal of Control, 2011, 84(5): 904-915
doi: 10.1080/00207179.2011.582886 |
| [15] |
Zhao D X, Wang J M. Exponential stability and spectral analysis of the inverted pendulum system under two delayed position feedbacks. Journal of Dynamical and Control Systems, 2012, 18(2): 269-295
doi: 10.1007/s10883-012-9143-6 |
| [16] | Atay F M. Balancing the inverted pendulum using position feedback. Applied Mathematics Letters, 1999, 12(5): 51-56 |
| [17] | Chentouf B, Smaoui N. Time-Delayed feedback control of a hydraulic model governed by a diffusive wave system. Complexity, 2020: Article ID 4986026 |
| [18] | 范东霞, 赵东霞, 史娜, 等. 一类扩散波方程的PDP反馈控制和稳定性分析. 数学物理学报, 2021, 41A(4): 1088-1096 |
| Fan D X, Zhao D X, Shi N, et al. The PDP feedback control and stability analysis of a diffusive wave equation. Acta Mathematica Scientia, 2021, 41A(4): 1088-1096 | |
| [19] |
庞玉婷, 赵东霞, 赵鑫, 等. 一类    |
Pang Y T, Zhao D X, Zhao X, et al. The PDP boundary control for a class of    |
| [1] |
Pang Yuting,Zhao Dongxia,Zhao Xin,Gao Caixia.
The PDP Boundary Control for a Class of 2 |
| [2] | He Xuyang,Mao Mingzhi,Zhang Tengfei. Existence and Stability of a Class of Impulsive Neutral Stochastic Functional Differential Equations with Poisson Jump [J]. Acta mathematica scientia,Series A, 2023, 43(4): 1221-1243. |
| [3] | Dongxia Fan,Dongxia Zhao,Na Shi,Tingting Wang. The PDP Feedback Control and Stability Analysis of a Diffusive Wave Equation [J]. Acta mathematica scientia,Series A, 2021, 41(4): 1088-1096. |
| [4] | Jian Liu,Zhixin Zhang,Wei Jiang. Global Mittag-Leffler Stability of Fractional Order Nonlinear Impulsive Differential Systems with Time Delay [J]. Acta mathematica scientia,Series A, 2020, 40(4): 1053-1060. |
| [5] | Xingshou Huang,Ricai Luo,Wusheng Wang. Stability Analysis for a Class Neural Network with Proportional Delay Based on the Gronwall Integral Inequality [J]. Acta mathematica scientia,Series A, 2020, 40(3): 824-832. |
| [6] | Chao Yang,Runjie Li. Existence and Stability of Periodic Solution for a Lasota-Wazewska Model with Discontinuous Harvesting [J]. Acta mathematica scientia,Series A, 2019, 39(4): 785-796. |
| [7] | Jian Dong. Research on the Application of Central Scheme in Saint-Venant System [J]. Acta mathematica scientia,Series A, 2019, 39(2): 372-385. |
| [8] | Xiong Jun, Li Junmin, He Chao. Fuzzy Boundary Control Design for a Class of First-Order Hyperbolic PDEs [J]. Acta mathematica scientia,Series A, 2017, 37(3): 469-477. |
| [9] | Zhang Liping, Liu Dongyi, Zhang Guoshan. Exponential Stabilization of a Timoshenko Beam System with Internal Disturbances [J]. Acta mathematica scientia,Series A, 2017, 37(1): 185-198. |
| [10] | Huang Zuda. Positive Pseudo Almost Periodic Solutions for a Delayed Nicholson's Blowflies Model with a Feedback Control [J]. Acta mathematica scientia,Series A, 2016, 36(3): 558-568. |
| [11] | Jiang Ani. Pseudo Almost Periodic Solutions for a Model of Hematopoiesis with an Oscillating Circulation Loss Rate [J]. Acta mathematica scientia,Series A, 2016, 36(1): 80-89. |
| [12] |
QIN Yu-Ming, LI Hai-Yan.
GLOBAL EXISTENCE AND EXPONENTIAL STABILITY OF SOLUTIONS TO THE QUASILINEAR THERMO-DIFFUSION EQUATIONS WITH SECOND SOUND [J]. Acta mathematica scientia,Series A, 2014, 34(3): 759-778. |
| [13] | ZHANG Yu-Tian, LUO Qi. Global Exponential Stability of Impulsive Reaction-Diffusion Cellular Neural Networks with Time-Varying Delays and Neumann Boundary Condition [J]. Acta mathematica scientia,Series A, 2013, 33(4): 777-786. |
| [14] | ZHANG Chun-Guo. Stability for the Nonhomogeneous Timoshenko Beam with Local Memory Damping [J]. Acta mathematica scientia,Series A, 2012, 32(1): 186-200. |
| [15] | ZHANG Ruo-Jun, WANG Lin-Shan. Almost Periodic Solutions for Cellular Neural Networks with Distributed Delays [J]. Acta mathematica scientia,Series A, 2011, 31(2): 422-429. |
| Viewed | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
Full text 208
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Abstract 115
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
Cited |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
| Shared | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Discussed | ||||||||||||||||||||||||||||||||||||||||||||||||||
|