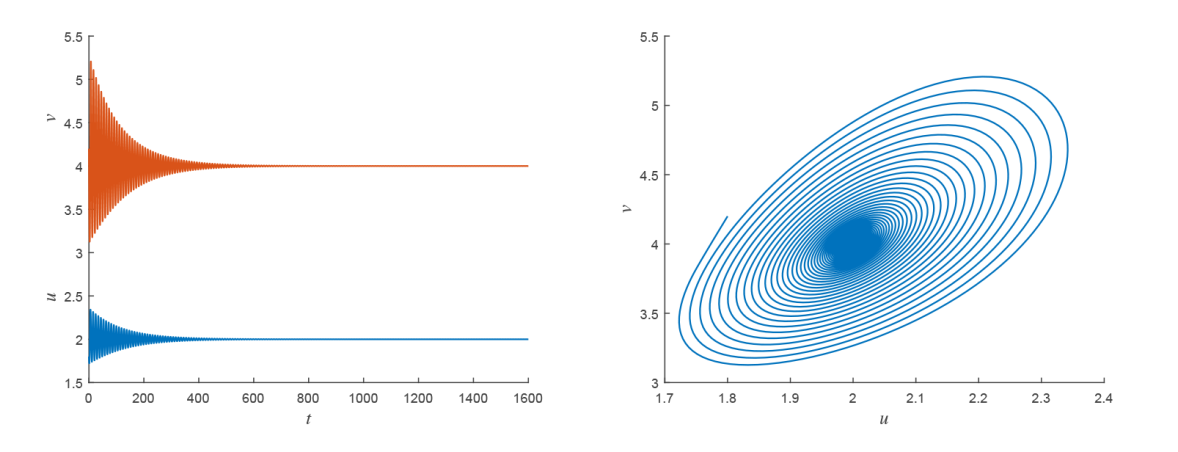
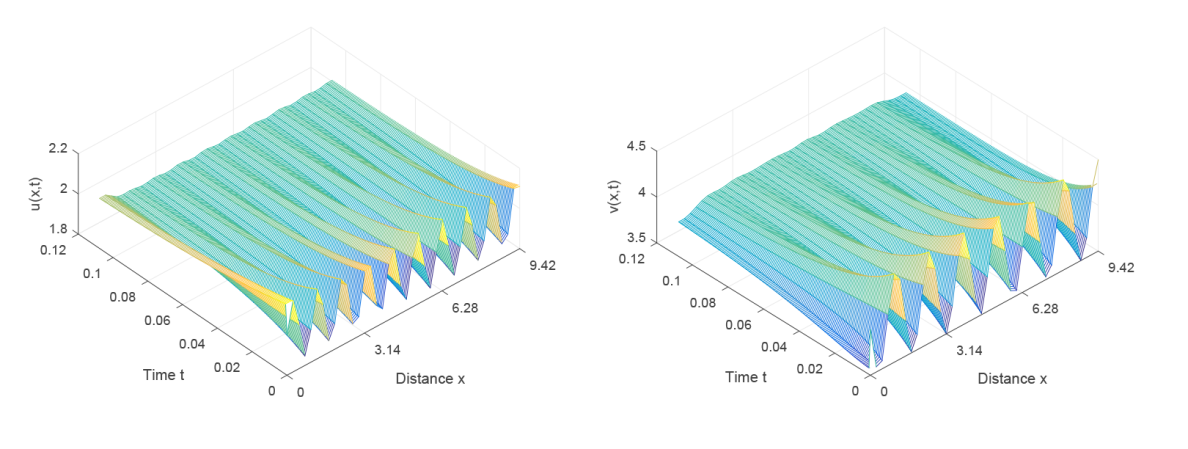
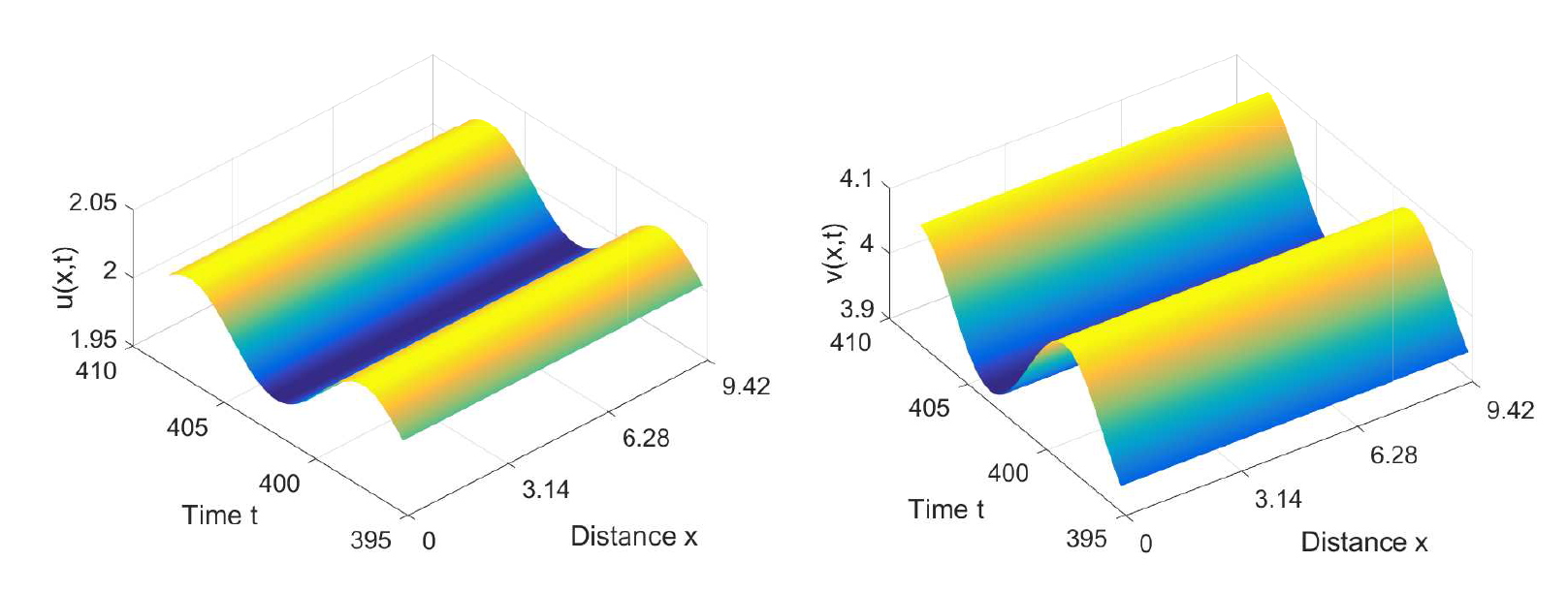
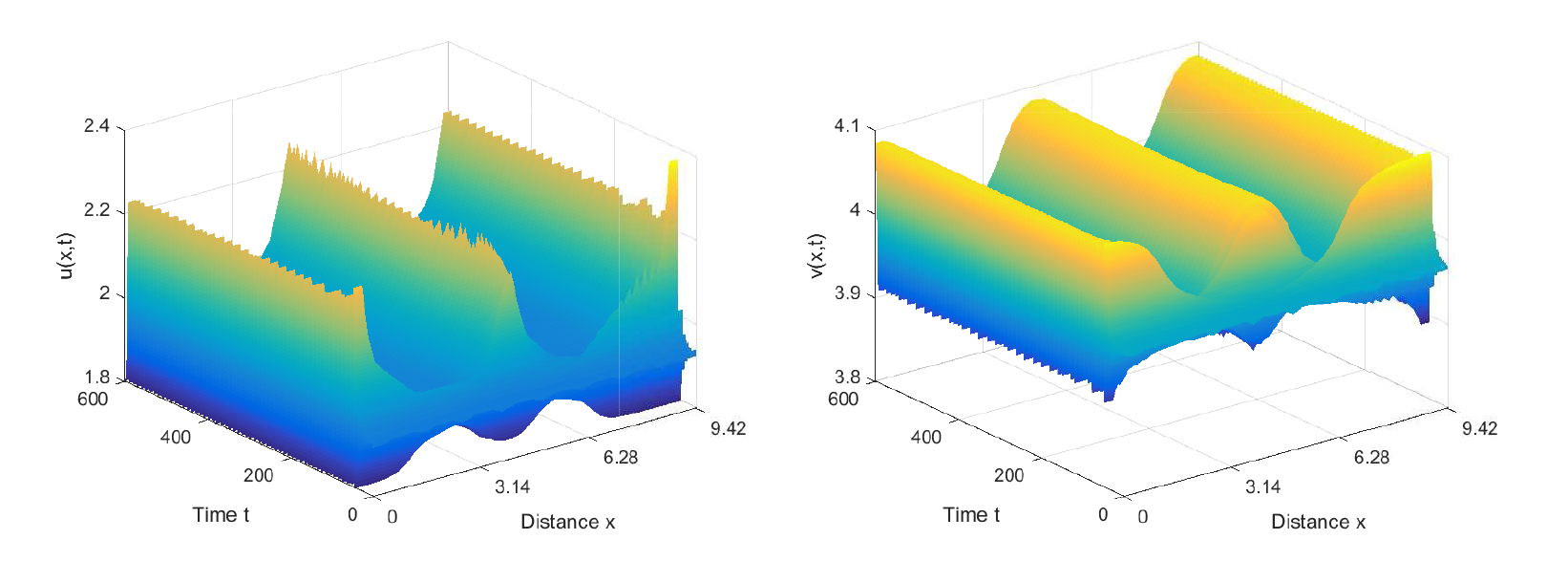
Acta mathematica scientia,Series A ›› 2023, Vol. 43 ›› Issue (6): 1774-1788.
Previous Articles Next Articles
Bifurcation Analysis of a Class of Gierer-Meinhardt Activation Inhibition Model with Time Delay
- 1School of Mathematics and Data Science, Shanxi University of Science and Technology, Xi'an 710021
2School of Mathematics and Statistics, Xi'an Jiaotong University, Xi'an 710049
-
Received:2022-08-08Revised:2023-07-07Online:2023-12-26Published:2023-11-16 -
Supported by:NSFC(11901370);Natural Science Basic Research Plan in Shannxi Province(2019JQ-516);Natural Science Foundation of Shanxi Provincial Department of Education grant(19JK0142);Natural Science Foundation of China(2019M653578);Shanxi Provincial Association for Science and Technology(20200508)
CLC Number:
- O175.12
Cite this article
Ma Yani, Yuan Hailong. Bifurcation Analysis of a Class of Gierer-Meinhardt Activation Inhibition Model with Time Delay[J].Acta mathematica scientia,Series A, 2023, 43(6): 1774-1788.
share this article
| [1] | 欧阳颀. 反应扩散系统中的斑图动力学. 上海: 上海科技教育出版社, 2000 |
| Ou Y X. Turing Dynamics in Reaction Diffusion Systems. Shanghai: Shanghai Science and Technology Education Press, 2000 | |
| [2] |
Gierer A, Meinhardt H. A theory of biological pattern formation. Kybernetik, 1972, 12: 30-39
pmid: 4663624 |
| [3] |
Gierer A, Meinhardt H. Application of a theory of biological pattern formation based on lateral inhibition. J Cell Sci, 1974, 15(2): 321-346
doi: 10.1242/jcs.15.2.321 pmid: 4859215 |
| [4] | Gierer A, Meinhardt H. Generation and regeneration of sequence of structures during morphogenesis. J Theor Biol, 1980, 3: 429-450 |
| [5] |
Wei J C, Winter M. Spikes for the Gierer-Meinhardt system in two dimensions: The strong coupling case. J Differ Equ, 2002, 178(2): 478-518
doi: 10.1006/jdeq.2001.4019 |
| [6] |
Ni W M, Suzuki K, Takagi I. The dynamics of a kinetic activator-inhibitor system. J Differ Equ, 2006, 229(2): 426-465
doi: 10.1016/j.jde.2006.03.011 |
| [7] |
Takashi M, Maini P K. Speed of pattern appearance in reaction-diffusion models: Implications in the pattern formation of limb bud mesenchyme cells. Bull Math Biol, 2004, 66(4): 627-649
doi: 10.1016/j.bulm.2003.09.009 |
| [8] |
Gonpot P, Collet J S A J, Sookia N U H. Gierer-Meinhardt model: Bifurcation analysis and pattern formation. Trends Appl Sci Res, 2008, 3: 115-128
doi: 10.3923/tasr.2008.115.128 |
| [9] |
Yang R, Song Y L. Spatial resonance and Turing-Hopf bifurcations in the Gierer-Meinhardt model. Nonlinear Anal: Real World Appl, 2016, 31: 356-387
doi: 10.1016/j.nonrwa.2016.02.006 |
| [10] | 杨文彬, 吴建华. 空间齐次和非齐次下活化-抑制模型动力学分析. 数学物理学报, 2017, 37A(22): 390-400 |
| Yang W B, Wu J H. Dynamics analysis of activation-inhibition models under spatial homogeneous and heterogeneou. Acta Math Sci, 2017, 37A(22): 390-400 | |
| [11] |
Liu J X, Yi F Q, Wei J J. Multiple bifurcation analysis and spatiotemporal patterns in a  doi: 10.1142/S0218127410026289 |
| [12] | Wang J L, Hou X J, Jing Z J. Stripe and spot patterns in a Gierer Meinhardt activator-inhibitor model with different sources. Int J Bifurcat Chaos, 2015, 25(8): 108-155 |
| [13] |
Wang J F, Wei J J, Shi J P. Global bifurcation analysis and pattern formation in homogeneous diffusive predator-prey systems. J Diff Equ, 2016, 260(4): 3495-3523
doi: 10.1016/j.jde.2015.10.036 |
| [14] | 叶其孝, 李正元, 王明新, 吴雅萍. 反应扩散方程引论. 北京: 科学出版社, 2011 |
| Ye Q X, Li Z Y, Wang M X, Wu Y P. Introduction to Reaction-Diffusion Equations. Beijing: Science Press, 2011 | |
| [15] |
Yi F Q, Wei J J, Shi J P. Diffusion-Driven instability and bifurcation in the Lengyel-Epstein system. Nonlinear Anal: Real World Appl, 2008, 9(3): 1038-1051
doi: 10.1016/j.nonrwa.2007.02.005 |
| [16] |
Galkhar S, Negi K, Sahani S K. Effects of seasonal growth on ratio dependent delayed prey predator system. Commun Nonlinear Sci Numer Simul, 2009, 14(3): 850-862
doi: 10.1016/j.cnsns.2007.10.013 |
| [17] |
Guan X N, Wang W M, Cai Y L. Spatiotemporal dynamics of a leslie-gower predator-prey model incorporating a prey refuge. Nonlinear Anal: Real World Appl, 2011, 12(4): 2385-2395
doi: 10.1016/j.nonrwa.2011.02.011 |
| [18] |
Lee S S, Gaffney E A, Monk N A M. The influence of gene expression time delays on Gierer-Meinhardt pattern formation systems. Bull Math Biol, 2010, 72(8): 2139-2160
doi: 10.1007/s11538-010-9532-5 |
| [19] |
Dutta S, Ray D S. Effects of delay in a reaction-diffusion system under the influence of an electric field. Phys Rev E, 2008, 77(3): 036202
doi: 10.1103/PhysRevE.77.036202 |
| [20] |
Ghosh P. Control of the Hopf-turing transition by time-delayed global feedback in a reaction-diffusion System. Phys Rev E, 2011, 84: 016222
doi: 10.1103/PhysRevE.84.016222 |
| [21] |
Ghosh P, Sen S, Ray D S. Reaction-Cattaneo systems with fluctuating relaxation time. Phys Rev E, 2010, 81(2): 026205
doi: 10.1103/PhysRevE.81.026205 |
| [22] |
Kyrychko Y, Blyuss K B, Hogan S J, et al. Control of spatiotemporal patterns in the Gray-Scott model. Chaos, 2009, 19(4): 043126
doi: 10.1063/1.3270048 |
| [23] |
Sen S, Ghosh P, Syed S, et al. Time-Delay-Induced instabilities in reaction diffusion systems. Phys Rev E, 2008, 80(4): 046212
doi: 10.1103/PhysRevE.80.046212 |
| [24] | Suleiman A L. Stability analysis of the Gierer-Meinhardt system with activator degradation. Dutse J Pure Appl Sci, 2016, 2(1): 48-54 |
| [25] |
Li C C, Guo S J. Stability and bifurcation of a delayed reaction-diffusion model with robin boundary condition in heterogeneous environment. Int J Bifurcat Chaos, 2023, 33(2): 2350018
doi: 10.1142/S0218127423500189 |
| [26] | Wen T T, Wang X L, Zhang G H. Hopf bifurcation in a two-species reaction-diffusion-advection competitive model with nonlocal delay. Commun Pur Appl Anal, 2023, 22(5): 1517-1544 |
| [27] | Ma L, Wei D. Hopf bifurcation of a delayed reaction-diffusion model with advection term. Nonlinear Anal: An Inter Mult J, 2021, 212(2): 112455 |
| [28] | 王雅迪, 袁海龙. 一类具有时滞的营养-微生物扩散模型的 Hopf 分支研究. 西南师范大学学报(自然科学版), 2023, 48(5): 1-13 |
| Wang Y D, Yuan H L. Hopf bifurcation of a nutritional microbial diffusion model with time delay. Journal of Southwest Normal University (Natural Science Edition), 2023, 48(5): 1-13 | |
| [29] |
Dong Y Y, Li S B, Zhang S L. Hopf bifurcation in a reaction-diffusion model with Degn-Harrison reaction scheme. Nonlinear Anal: Real World Appl, 2017, 33: 284-297
doi: 10.1016/j.nonrwa.2016.07.002 |
| [30] | Lin X D, So J W H, Wu J H. Center manifolds for partial differential equations with delay. P Roy Soc Edinb A: Math, 1992, 122(3/4): 237-254 |
| [31] | Wu J H. Theory and Applications of Partial Functional Differential Equations. New York: Springer-Verlag, 1996 |
| [32] | 万阿英, 衣风岐, 郑立飞. 一类扩散的 Gierer-Meinhardt 的模型的振动模式和 Hopf 分支分析. 数学物理学报, 2015, 35A(2): 381-394 |
| Wan A Y, Yi F Q, Zeng L F. Oscillating patterns and Hopf bifurcation analysis of a class of diffusion Gierer-Meinhardt models. Acta Math Sci, 2015, 35A(2): 381-394 |
| [1] | Xu Fei, Zhang Yong. Uniqueness and Asymptotic Stability of Time-Periodic Solutions for the Fractional Burgers Equation [J]. Acta mathematica scientia,Series A, 2023, 43(6): 1710-1722. |
| [2] | Pang Yuting, Zhao Dongxia. The PDP Feedback Control and Exponential Stabilization of a Star-Shaped Open Channels Network System [J]. Acta mathematica scientia,Series A, 2023, 43(6): 1803-1813. |
| [3] | Fan Shishi, Li Haixia, Lu Yindou. Dynamics Analysis of a Diffusive Predator-Prey Model with Beddington-DeAngelis Function Response and Harvesting [J]. Acta mathematica scientia,Series A, 2023, 43(6): 1929-1942. |
| [4] |
Pang Yuting,Zhao Dongxia,Zhao Xin,Gao Caixia.
The PDP Boundary Control for a Class of 2 |
| [5] | Liao Yuankang. Nonlinear Stability of Viscous Shock Waves for One-dimensional Isentropic Compressible Navier-Stokes Equations with Density-Dependent Viscosity [J]. Acta mathematica scientia,Series A, 2023, 43(4): 1149-1169. |
| [6] | He Xuyang,Mao Mingzhi,Zhang Tengfei. Existence and Stability of a Class of Impulsive Neutral Stochastic Functional Differential Equations with Poisson Jump [J]. Acta mathematica scientia,Series A, 2023, 43(4): 1221-1243. |
| [7] | Li Jize,Qiu Jixiu,Zhou Yonghui. Anticipative Nonlinear Filtering Equations Affected by Observation Noises and Stability of Linear Filtering [J]. Acta mathematica scientia,Series A, 2023, 43(4): 1244-1254. |
| [8] | Zhang Haiqun. Bounded Rationality and Stability of Weakly Efficient Nash Equilibria for a Class of Population Games [J]. Acta mathematica scientia,Series A, 2023, 43(4): 1311-1320. |
| [9] | Li Xiaoli,Chen Xiaoli. Stability and Exponential Decay of the 3D Boussinesq Equations with Partial Dissipation [J]. Acta mathematica scientia,Series A, 2023, 43(3): 754-770. |
| [10] | Wu Wenjun,Yang Guanghui,Fang Caiya,Yang Hui. Generic Stability of Cooperative Equilibria for Leader-Follower Population Games [J]. Acta mathematica scientia,Series A, 2023, 43(3): 921-929. |
| [11] | Kang Xiaodong, Fan Hongxia. Approximate Controllability for a Class of Second-Order Evolution Equations with Instantaneous Impulse [J]. Acta mathematica scientia,Series A, 2023, 43(2): 421-432. |
| [12] | Fu Qinhong, Xiong Lianglin, Zhang Haiyang, Qin Ya, Quan Shenai. Sliding Mode Control for Time-Varying Delay Systems with Semi-Markov Jump [J]. Acta mathematica scientia,Series A, 2023, 43(2): 549-562. |
| [13] | Liu Lili, Wang Honggang, Li Yazhi. A Generalized HBV Diffusive Model with DNA-Containing Capsids and Cell-Cell Infection [J]. Acta mathematica scientia,Series A, 2023, 43(2): 604-624. |
| [14] | Song Huijuan, Huang Qian, Wang Zejia. Asymptotic Analysis of a Tumor Model with Angiogenesis and a Periodic Supply of External Nutrients [J]. Acta mathematica scientia,Series A, 2023, 43(1): 261-273. |
| [15] | Ming Han. E-Bayesian Estimation and E-MSE of Failure Probability and Its Applications [J]. Acta mathematica scientia,Series A, 2022, 42(6): 1790-1801. |
| Viewed | ||||||||||||||||||||||||||||||||||||||||||||||
|
Full text 218
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Abstract 95
|
|
|||||||||||||||||||||||||||||||||||||||||||||
Cited |
|
|||||||||||||||||||||||||||||||||||||||||||||
| Shared | ||||||||||||||||||||||||||||||||||||||||||||||
| Discussed | ||||||||||||||||||||||||||||||||||||||||||||||
|