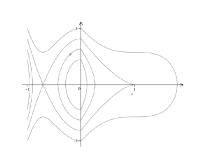
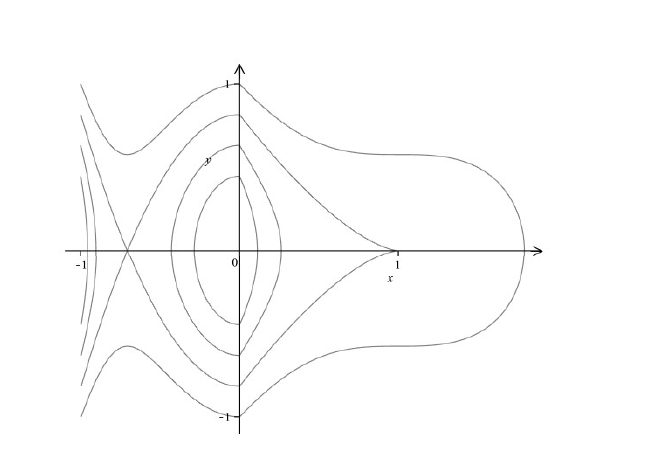
Acta mathematica scientia,Series A ›› 2023, Vol. 43 ›› Issue (6): 1667-1680.
Previous Articles Next Articles
Limit Cycle Bifurcations of a Non-smooth Differential System with a Cuspidal Loop
- School of Mathematics and Computer Science, Ningxia Normal University, Ningxia Guyuan 756000
-
Received:2022-11-22Revised:2023-05-17Online:2023-12-26Published:2023-11-16 -
Supported by:NSFC(12161069);Natural Science Foundation of Ningxia(2022AAC05044);Construction of First-class Disciplines of Higher Education of Ningxia (pedagogy)(NXYLXK2021B10)
CLC Number:
- O175.12
Cite this article
Yang Jihua, Ma Liang. Limit Cycle Bifurcations of a Non-smooth Differential System with a Cuspidal Loop[J].Acta mathematica scientia,Series A, 2023, 43(6): 1667-1680.
share this article
| [1] |
Tse C, Bernardo M. Complex behavior in switching power converter. Proceeding of IEEE, 2002, 90(5): 768-781
doi: 10.1109/JPROC.2002.1015006 |
| [2] |
Kember S, Babitsky V. Excitation of vibro-impact systems by periodic impulses. J Sound Vib, 1999, 227(2): 427-447
doi: 10.1006/jsvi.1999.2353 |
| [3] | 黄立宏, 郭振远, 王佳伏. 右端不连续微分方程理论与应用. 北京: 科学出版社, 2011 |
| Huang L H, Guo Z Y, Wang F J. Theory and Application of Differential Equations with Discontinuous Right-Hand Sides. Beijing: Science Press, 2011 | |
| [4] |
Zou Y, Kupper T, Beyn W. Generalized Hopf bifurcation for planar Filippov systems continuous at the origin. J Nonlinear Sci, 2006, 16(2): 159-177
doi: 10.1007/s00332-005-0606-8 |
| [5] |
Simpson D, Meiss J. Andronov-Hopf bifurcation in planar, piecewise-smooth, continuous flows. Phys Lett A, 2007, 371(3): 213-220
doi: 10.1016/j.physleta.2007.06.046 |
| [6] |
Virgin L, Begley C. Grazing bifurcations and basins of attraction in an impact-friction oscillator. Physica D, 1999, 130: 43-57
doi: 10.1016/S0167-2789(99)00016-0 |
| [7] |
Kukučka P. Melnikov method for discontinuous planar systems. Nonlinear Anal, 2007, 66: 2698-2719
doi: 10.1016/j.na.2006.04.001 |
| [8] |
Li L, Huang L. Concurrent homoclinic bifurcation and Hopf bifurcation for a class of planar Filippov systems. J Math Anal Appl, 2014, 411: 83-94
doi: 10.1016/j.jmaa.2013.09.025 |
| [9] |
Liu X, Han M A. Bifurcation of limit cycles by perturbing piecewise Hamiltonian systems. Int J Bifurc Chaos, 2010, 20(5): 1379-1390
doi: 10.1142/S021812741002654X |
| [10] |
Llibre J, Lopes B, Moraes J. Limit cycles for a class of continuous and discontinuous cubic polynomial differential systems. Qual Theory Dyn Syst, 2014, 13: 129-148
doi: 10.1007/s12346-014-0109-9 |
| [11] |
Li F, Yu P, Tian Y, Liu Y. Center and isochronous center conditions for switching systems associated with elementary singular points. Commun Nonlinear Sci Numer Simul, 2015, 28: 81-97
doi: 10.1016/j.cnsns.2015.04.005 |
| [12] |
Guo L, Yu P, Chen Y. Bifurcation analysis on a class of   doi: 10.1016/j.jde.2018.07.071 |
| [13] |
Liang F, Han M. Limit cycles near generalized homoclinic and double homoclinic loops in piecewise smooth systems. Chaos Solitons Fractals, 2012, 45: 454-464
doi: 10.1016/j.chaos.2011.09.013 |
| [14] |
Liang F, Han M, Zhang X. Bifurcation of limit cycles from generalized homoclinic loops in planar piecewise smooth systems. J Differential Equations, 2013, 255: 4403-4436
doi: 10.1016/j.jde.2013.08.013 |
| [15] |
Xiong Y, Han M. Limit cycles appearing from a generalized heteroclinic loop with a cusp and a nilpotent saddle. J Differential Equations, 2021, 303: 575-607
doi: 10.1016/j.jde.2021.09.031 |
| [16] | Han M, Sheng L. Bifurcation of limit cycles in piecewise smooth systems via Melnikov function. J Appl Anal Comput, 2015, 5: 809-815 |
| [1] | Xueli Jiang,Xuan Deng,Qiuhao Wen,Yanqin Xiong. Limit Circle Bifurcations of Polynomial Differential System with Two Parallel Switch Straight Lines [J]. Acta mathematica scientia,Series A, 2022, 42(2): 353-364. |
| [2] |
Zhiqiang Gao.
A Second Order Correction of the Local Limit Theorem for a Branching Random Walk with a Random Environment in Time on   |
| [3] | Hongying Zhu,Minzhi Wei,Sumin Yang,Caoqing Jiang. Bifurcation of Limit Cycles from a Liénard System of Degree 4 [J]. Acta mathematica scientia,Series A, 2021, 41(4): 936-953. |
| [4] | Yi Shao,Chunxiang A. Limit Cycles Bifurcations of Liénard System of Degree Four with One Nilpotent Cusp [J]. Acta mathematica scientia,Series A, 2020, 40(3): 619-630. |
| [5] | Ru Wang,Zhonghua Zhang,Yeling Liu. Dynamical Properties of a Discontinuous Models with Signal Molecules Regulation [J]. Acta mathematica scientia,Series A, 2019, 39(6): 1545-1554. |
| [6] | Kun Zhu,Jianhe Shen. A Revisit on Multiple-Pulse Homoclinic Solutions in a Generalized Gierer-Meinhardt Equation [J]. Acta mathematica scientia,Series A, 2019, 39(6): 1365-1375. |
| [7] | Liao Shupeng, Shen Jianhe. One-Pulse Travelling Front Solutions of a sine-Gordon Equation with Slowly Varying Parameters [J]. Acta mathematica scientia,Series A, 2018, 38(4): 810-822. |
| [8] | Liang Zhiqing, Zeng Xiaping, Zhou Zewen, Pang Guoping, Huang Junhua. Existence of Periodic Solution of Holling-Tanner System with State Feedback Impulsive Control [J]. Acta mathematica scientia,Series A, 2018, 38(1): 174-189. |
| [9] | Liang Haihua, Chen Yuming, Cen Xiuli. Limit Cycles Bifurcating from a Class of Quasi-Homogeneous Polynomial Center [J]. Acta mathematica scientia,Series A, 2018, 38(1): 1-9. |
| [10] | Zhang Erli, Xing Yuqing. Limit Cycle Bifurcations for a Kind of Hamilton Systems of Degree Three [J]. Acta mathematica scientia,Series A, 2017, 37(5): 825-833. |
| [11] | Yang Wenbin, Wu Jianhua. Some Dynamics in Spatial Homogeneous and Inhomogeneous Activator-Inhibitor Model [J]. Acta mathematica scientia,Series A, 2017, 37(2): 390-400. |
| [12] | Li Shimin, Cen Xiuli. Limit Cycles for Perturbing Quadratic Isochronous Center Inside Discontinuous Quadratic Polynomial Differential System [J]. Acta mathematica scientia,Series A, 2016, 36(5): 919-927. |
| [13] | SHANG De-Sheng, ZHANG Yao-Ming. Global Bifurcation of A Symmetric Cubic System [J]. Acta mathematica scientia,Series A, 2015, 35(1): 83-96. |
| [14] | WU Kui-Lin, SHAO Yi. Quadratic Perturbations of a Quadratic Reversible Lotka-Volterra System of Genus One with Two Centers [J]. Acta mathematica scientia,Series A, 2014, 34(5): 1275-1286. |
| [15] | JIN Shan, LU Shi-Ping. Uniqueness and Bifurcation of Limit Cycles for a Class of Polynomical System [J]. Acta mathematica scientia,Series A, 2011, 31(6): 1669-1673. |
| Viewed | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
Full text 121
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Abstract 104
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
Cited |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
| Shared | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Discussed | ||||||||||||||||||||||||||||||||||||||||||||||||||