Acta mathematica scientia,Series A ›› 2023, Vol. 43 ›› Issue (1): 249-260.
Previous Articles Next Articles
Parameter Estimation for Nonlinear Stochastic Differential Equations Driven by 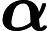
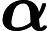
Zhang Xuekang1,*( ),Wan Shanlin1(
),Wan Shanlin1( ),Shu Huisheng2(
),Shu Huisheng2( )
)
- 1School of Mathematics-Physics and Finance, Anhui Polytechnic University, Anhui Wuhu 241000
2College of Science, Donghua University, Shanghai 201620
-
Received:2021-04-22Revised:2022-07-05Online:2023-02-26Published:2023-03-07 -
Supported by:The NSFC(12101004);The NSFC(62073071);The NSFC(12271003);Startup Foundation for Introducing Talent of Anhui Polytechnic University(2020YQQ064);Open Project of Anhui Province Center for International Reasearch of Intelligent Control of High-end Equipment(IRICHE-05)
CLC Number:
- O211
Cite this article
Zhang Xuekang, Wan Shanlin, Shu Huisheng. Parameter Estimation for Nonlinear Stochastic Differential Equations Driven by 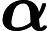
share this article
| [1] | Applebaum D. Lévy Processes and Stochastic Calculus. United Kingdom: Cambridge University Press, 2009 |
| [2] | Basawa I, Scott D. Asymptotic Optimal inference for Non-ergodic Models. New York: Springer, 1983 |
| [3] |
Bercu B, ProÏa F, Savy N. On Ornstein-Uhlenbeck driven by Ornstein-Uhlenbeck processes. Statist Probab Lett, 2014, 85: 36-44
doi: 10.1016/j.spl.2013.11.002 |
| [4] |
Bo L, Wang Y, Yang X, Zhang G. Maximum likelihood estimation for reflected Ornstein-Uhlenbeck processes. J Statist Plann Inference, 2011, 141: 588-596
doi: 10.1016/j.jspi.2010.07.001 |
| [5] |
Dietz H. Asymptotic behavior of trajectory fitting estimators for certain non-ergodic SDE. Stat Inference Stoch Process, 2001, 4: 249-258
doi: 10.1023/A:1012254332474 |
| [6] | Dietz H, Kutoyants Y. A class of minimum-distance estimators for diffusion processes with ergodic properties. Stat Decis, 1997, 15: 211-227 |
| [7] | Dietz H, Kutoyants Y. Parameter estimation for some non-recurrent solutions of SDE. Stat Decis, 2003, 21: 29-45 |
| [8] |
Fama E. Mandelbrot and the stable Paretian hypothesis. J Business, 1963, 36: 420-429
doi: 10.1086/294633 |
| [9] |
Hu Y, Long H. Parameter estimation for Ornstein-Uhlenbeck processes driven by  |
| [10] |
Hu Y, Long H. Least squares estimator for Ornstein-Uhlenbeck processes driven by  doi: 10.1016/j.spa.2008.12.006 |
| [11] |
Hu Y, Long H. On the singularity of least squares estimator for mean-reverting  |
| [12] |
Janicki A, Weron A. Simulation and Chaotic Behavior of  |
| [13] | Jeong H, Tomber B, Albert R, et al. The large-scale organization of metabolic networks. Nature, 2000, 407: 378-382 |
| [14] |
Jiang H, Dong X. Parameter estimation for the non-stationary Ornstein-Uhlenbeck process with linear drift. Stat Papers, 2015, 56: 257-268
doi: 10.1007/s00362-014-0580-z |
| [15] |
Kessler M. Estimation of an ergodic diffusion from discrete observations. Scand J Statist, 1997, 24: 211-229
doi: 10.1111/1467-9469.00059 |
| [16] | Kutoyants Y. Statistical Inference for Ergodic Diffusion Processes. Heidelberg: Springer-Verlag, 2004 |
| [17] | Long H. Parameter estimation for a class of stochastic differential equations driven by small stable noises from discrete observations. Acta Math Sci, 2010, 30B(3): 645-663 |
| [18] |
Mandelbrot B. The Pareto-Lévy law and the distribution of income. Int Econ Rev, 1960, 1: 79-106
doi: 10.2307/2525289 |
| [19] |
Pan Y, Yan L. The least squares estimation for the  doi: 10.1007/s11009-018-9654-z |
| [20] | Sato K. Lévy Processes and Infinitely Divisible Distributions. Cambridge: Cambridge University Press, 1999 |
| [21] |
Shimizu Y. Local asymptotic mixed normality for discretely observed non-recurrent Ornstein-Uhlenbeck processes. Ann Inst Stat Math, 2012, 64: 193-211
doi: 10.1007/s10463-010-0307-4 |
| [22] |
Xu W, Wu C, Dong Y, Xiao W. Modeling Chinese stock returns with stable distribution. Math Comput Model, 2011, 54: 610-617
doi: 10.1016/j.mcm.2011.03.004 |
| [23] |
Zang Q, Zhang L. Asymptotic behaviour of the trajectory fitting estimator for reflected Ornstein-Uhlenbeck Processes. J Theor Probab, 2019, 32: 183-201
doi: 10.1007/s10959-017-0796-7 |
| [24] |
Zang Q, Zhu C. Asymptotic behaviour of parametric estimation for nonstationary reflected Ornstein-Uhlenbeck processes. J Math Anal Appl, 2016, 444: 839-851
doi: 10.1016/j.jmaa.2016.06.067 |
| [25] |
Zhang S, Zhang X. A least squares estimator for discretely observed Ornstein-Uhlenbeck processes driven by symmetric  doi: 10.1007/s10463-012-0362-0 |
| [26] |
Zhang X, Yi H, Shu H. Nonparametric estimation of the trend for stochastic differential equations driven by small  doi: 10.1016/j.spl.2019.03.012 |
| [27] |
Zhang X, Yi H, Shu H. Parameter estimation for non-stationary reflected Ornstein-Uhlenbeck processes driven by  doi: 10.1016/j.spl.2019.108617 |
| [28] |
Zhang X, Yi H, Shu H. Parameter estimation for certain nonstationary processes driven by  doi: 10.1080/03610926.2019.1630436 |
| [29] | Zolotarev V. One-Dimensional Stable Distribution. Providence: American Mathematical Society, 1986 |
| [1] | Chen Fei,Weiyin Fei. Consistency of Least Squares Estimation to the Parameter for Stochastic Differential Equations Under Distribution Uncertainty [J]. Acta mathematica scientia,Series A, 2019, 39(6): 1499-1513. |
| [2] | Wang Jixia, Xiao Qingxian. Local Estimation of the Diffusion Coefficient for Time-Inhomogeneous Diffusion Models [J]. Acta mathematica scientia,Series A, 2015, 35(2): 332-344. |
| [3] | TAO Bao. Asymptotic Properties of the Negative Extreme-value Index Estimator [J]. Acta mathematica scientia,Series A, 2014, 34(3): 611-618. |
| [4] | WANG Cheng-Yong. A Semiparametric Smooth Transition Regression Model and Its Series Estimator [J]. Acta mathematica scientia,Series A, 2012, 32(4): 797-807. |
| [5] | WANG Hong-Ning, YU Huan-Ran. Robust Nonparametric Regression with Simultaneous Scale Curve Estimation Based on Dependent Observations [J]. Acta mathematica scientia,Series A, 2010, 30(3): 835-847. |
| [6] | ZHANG Jun-Jian, LI Guo-Ying. Supremum-type Tests for Goodness-of-fit [J]. Acta mathematica scientia,Series A, 2010, 30(2): 344-357. |
| [7] | ZHANG Juan, CUI Heng-Jian. Weighted Adjust LS Estimation |in EV Model with Missing Data [J]. Acta mathematica scientia,Series A, 2009, 29(6): 1465-1476. |
| [8] | YIN Chang-Ming, LI Yong-Ming, WANG Peng-Yan. Strong Convergence Rates of the Maximum Quasi-Likelihood Estimator in Generalized Linear Models [J]. Acta mathematica scientia,Series A, 2009, 29(4): 1058-1064. |
| [9] | LI Li-Na, GAO Fu-Qing. Rates of Strong Uniform Consistency for Kernel Density Estimators of Directional Data [J]. Acta mathematica scientia,Series A, 2009, 29(3): 707-715. |
| [10] |
Xiao Zhihong;Liu Luqin.
MLE of Generalized Linear Model Randomly Censored with Incomplete Information [J]. Acta mathematica scientia,Series A, 2008, 28(3): 553-564. |
| [11] |
Li Guoliang; Liu Luqin.
Strong Consistency of a Class of Estimators in Partial Linear Model under Martingale Difference Sequence [J]. Acta mathematica scientia,Series A, 2007, 27(5): 788-801. |
| [12] | Xia Tian; Tang Niansheng; Wang Xueren; Zhang Wenzhuan. Asymptotic Properties in Nonlinear Reproductive Dispersion Models with Random Effects [J]. Acta mathematica scientia,Series A, 2007, 27(1): 146-154. |
| [13] | Ding Jieli;Chen Xiru. Strong Consistency of the Maximum Likelihood Estimator in Generalized Linear Models [J]. Acta mathematica scientia,Series A, 2006, 26(2): 168-173. |
| [14] | TUN Qun-Yang. Strong Consistency of M Estimator in Linear Model for rho mixing Samples [J]. Acta mathematica scientia,Series A, 2005, 25(1): 41-46. |
| [15] | HU Gen-Qi, FENG De-Xin. Uniform Stabilization of Timoshenko Beams with Boundary Feedba ck Control [J]. Acta mathematica scientia,Series A, 2003, 23(6): 719-728. |
| Viewed | ||||||||||||||||||||||||||||||||||||||||||||||
|
Full text 95
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Abstract 60
|
|
|||||||||||||||||||||||||||||||||||||||||||||
Cited |
|
|||||||||||||||||||||||||||||||||||||||||||||
| Shared | ||||||||||||||||||||||||||||||||||||||||||||||
| Discussed | ||||||||||||||||||||||||||||||||||||||||||||||
|