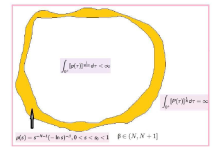
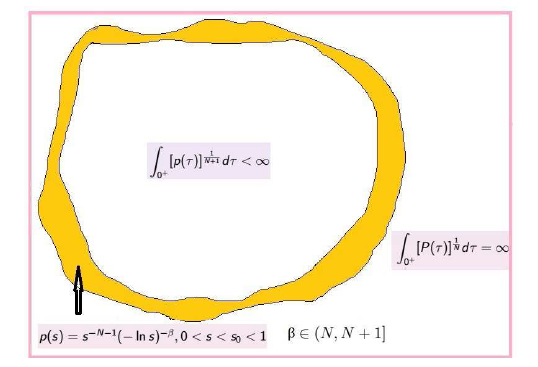
Acta mathematica scientia,Series A ›› 2023, Vol. 43 ›› Issue (1): 181-202.
Previous Articles Next Articles
On the Optimal Global Estimates of Boundary Blow-up Solutions to the Monge-Ampère Equation
Feng Meiqiang1,*( ),Zhang Xuemei2(
),Zhang Xuemei2( )
)
- 1School of Applied Science, Beijing Information Science & Technology University, Beijing 100192
2School of Mathematics and Physics, North China Electric Power University, Beijing 102206
-
Received:2021-11-24Revised:2022-04-24Online:2023-02-26Published:2023-03-07 -
Supported by:Beijing Natural Science Foundation of China(1212003)
CLC Number:
- O177.91
Cite this article
Feng Meiqiang, Zhang Xuemei. On the Optimal Global Estimates of Boundary Blow-up Solutions to the Monge-Ampère Equation[J].Acta mathematica scientia,Series A, 2023, 43(1): 181-202.
share this article
| [1] |
Bieberbach L.      doi: 10.1007/BF01456901 |
| [2] | Bingham N H, Goldie C M, Teugels J L. Regular Variation, Encyclopedia Math Appl. Cambridge: Cambridge University Press, 1987 |
| [3] |
Caffarelli L. Interior     doi: 10.2307/1971510 |
| [4] |
Caffarelli L, Nirenberg L, Spruck J. The Dirichlet problem for nonlinear second-order elliptic equations I. Monge-Ampère equations. Comm Pure Appl Math, 1984, 37: 369-402
doi: 10.1002/cpa.3160370306 |
| [5] |
Cheng S Y, Yau S T. On the regularity of the Monge-Ampère equation                         doi: 10.1002/cpa.3160300104 |
| [6] |
Cheng S Y, Yau S T. On the existence of a complete Kähler metric on noncompact complex manifolds and the regularity of Fefferman's equation. Comm Pure Appl Math, 1980, 33: 507-544
doi: 10.1002/cpa.3160330404 |
| [7] | Cheng S Y, Yau S T. The real Monge-Ampère equation and affine flat structures//Chern S S, Wu W. Proceedings of 1980 Beijing Symposium on Differential Geometry and Differential Equations, Vol 1. Beijing: Science Press, 1982: 339-370 |
| [8] |
Chuaqui M, Cortázar C, Elgueta M, Flores C, García-Melián J, Letelier R. On an elliptic problem with boundary blow-up and a singular weight: the radial case. Proc Roy Soc Edinburgh, 2003, 133: 1283-1297
doi: 10.1017/S0308210500002936 |
| [9] |
C  doi: 10.1007/s00526-007-0108-7 |
| [10] | Du Y. Order Structure and Topological Methods in Nonlinear Partial Differential Equations. Singapore: World Scientific, 2006 |
| [11] |
García-Melián J. Boundary behavior for large solutions to elliptic equations with singular weights. Nonlinear Anal, 2007, 67: 818-826
doi: 10.1016/j.na.2006.06.041 |
| [12] |
Gladiali F, Porru G. Estimates for explosive solutions to  |
| [13] |
Guan B, Jian H. The Monge-Ampère equation with infinite boundary value. Pacific J Math, 2004, 216: 77-94
doi: 10.2140/pjm.2004.216.77 |
| [14] |
Jian H, Wang X, Zhao Y. Global smoothness for a singular Monge-Ampère equation. J Differential Equations, 2017, 263: 7250-7262
doi: 10.1016/j.jde.2017.08.004 |
| [15] | Karamata J. Sur un mode de croissance régulière. Théorèmes fondamentaux. Bull Soc Math France, 1993, 61: 55-62 |
| [16] |
Keller J B. On solutions of        doi: 10.1002/cpa.3160100402 |
| [17] |
Lazer A C, McKenna P J. On singular boundary value problems for the Monge-Ampère operator. J Math Anal Appl, 1996, 197: 341-362
doi: 10.1006/jmaa.1996.0024 |
| [18] |
Matero J. The Bieberbach-Rademacher problem for the Monge-Ampère operator. Manuscripta Math, 1996, 91: 379-391
doi: 10.1007/BF02567962 |
| [19] |
Mohammed A. On the existence of solutions to the Monge-Ampère equation with infinite boundary values. Proc Amer Math Soc, 2007, 135: 141-149
doi: 10.1090/S0002-9939-06-08623-0 |
| [20] |
Mohammed A. Existence and estimates of solutions to a singular Dirichlet problem for the Monge-Ampère equation. J Math Anal Appl, 2008, 340: 1226-1234
doi: 10.1016/j.jmaa.2007.09.014 |
| [21] | Olofsson A. Apriori estimates of Osserman-Keller type. Differ Integral Equ, 2003, 16: 737-756 |
| [22] |
Osserman R. On the inequality       doi: 10.2140/pjm.1957.7.1641 |
| [23] | Pogorelov A V. The Multidimensional Minkowski Problem. New York: Wiley, 1978. |
| [24] | Rademacher H. Einige Besondere Probleme Partieller Differentialgleichungen, in: Die Differential- und Integralgleichungen, der Mechanik und Physikl. New York: Rosenberg, 1943 |
| [25] |
Savin O. Pointwise     doi: 10.1090/S0894-0347-2012-00747-4 |
| [26] | Seneta E. Regular Varying Functions, Lecture Notes in Math. Heidelberg: Springer-Verlag, 1976 |
| [27] |
Trudinger N, Wang X. Boundary regularity for the Monge-Ampère and affine maximal surface equations. Ann Math, 2008, 167: 993-1028
doi: 10.4007/annals.2008.167.993 |
| [28] |
Tso K. On a real Monge-Ampère functional. Invent Math, 1990, 101: 425-448
doi: 10.1007/BF01231510 |
| [29] | Wan H, Shi Y, Liu W. Refined second boundary behavior of the unique strictly convex solution to a singular Monge-Ampère equation. Adv Nonlinear Anal, 2022, 11: 321-356 |
| [30] | Yang H, Chang Y. On the blow-up boundary solutions of the Monge-Ampère equation with singular weights. Commun Pure Appl Anal, 2012, 11: 697-708 |
| [31] |
Zhang X, Du Y. Sharp conditions for the existence of boundary blow-up solutions to the Monge-Ampère equation. Calc Var Partial Differential Equations, 2018, 57: 30
doi: 10.1007/s00526-018-1312-3 |
| [32] | Zhang X, Feng M. Boundary blow-up solutions to the Monge-Ampère equation: Sharp conditions and asymptotic behavior. Adv Nonlinear Anal, 2020, 9: 729-744 |
| [33] |
Zhang X, Feng M. The existence and asymptotic behavior of boundary blow-up solutions to the  doi: 10.1016/j.jde.2019.05.004 |
| [34] |
Zhang Z. Optimal global and boundary behavior of large solutions to the Monge-Ampère equation. J Funct Anal, 2020, 278: 108512
doi: 10.1016/j.jfa.2020.108512 |
| [35] |
Zhang Z. Boundary behavior of large solutions to the Monge-Ampère equations with weights. J Differential Equations, 2015, 259: 2080-2100
doi: 10.1016/j.jde.2015.03.040 |
| [1] | Ting Ji,Lianggen Hu,Jing Zeng. The Non-Existence of Non-Radial Blow-Up Solutions for the Quasilinear Elliptic System [J]. Acta mathematica scientia,Series A, 2019, 39(2): 307-315. |
| [2] | SHEN Ji-Hong, ZHANG Ming-You, YANG Yan-Bing, LIU Bo-Wei, XU Run-Zhang. Global Well-posedness of Cauchy Problem for Damped Multidimensional Generalized Boussinesq Equations [J]. Acta mathematica scientia,Series A, 2014, 34(5): 1173-1187. |
| [3] | YU Dan-Sheng, ZHOU Song-Ping. Global and Pointwise Estimates for Approximation by Rational Functions with Polynomials of Positive Coefficients as the Denominators [J]. Acta mathematica scientia,Series A, 2011, 31(2): 305-319. |
| [4] | JIN Yong-Yang. Nonexistence Results for a Class of Sub-P-Laplacians [J]. Acta mathematica scientia,Series A, 2009, 29(5): 1434-1441. |
| [5] | LUO Zhen-Dong. The Global |Estimates of Least -squares |Mixed |Finite |Element for Elasticity Problems [J]. Acta mathematica scientia,Series A, 2000, 20(zk): 589-596. |
| Viewed | ||||||||||||||||||||||||||||||||||||||||||||||
|
Full text 107
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Abstract 90
|
|
|||||||||||||||||||||||||||||||||||||||||||||
Cited |
|
|||||||||||||||||||||||||||||||||||||||||||||
| Shared | ||||||||||||||||||||||||||||||||||||||||||||||
| Discussed | ||||||||||||||||||||||||||||||||||||||||||||||
|