一类四次扰动Liénard系统的极限环分支

Abstract

Abstract:

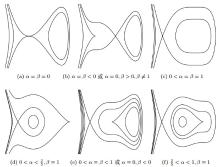
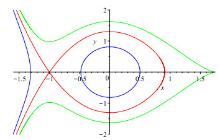
In this paper, we study the number of limit cycles by Poincaré bifurcation for some Liénard system of degree 4. We prove that the system can bifurcate at most 6 limit cycles from the periodic annulus, by the tools of regular chain theory in polynomial algebra and Chebyshev criteria, at least 3 limit cycles by asymptotic expansions of the related Abelian integral (first order Melnikov functions).

Key words: Liénard system, Chebyshev system, Melnikov functions, Weak Hilbert's 16th problem

CLC Number:

O175.12

Hongying Zhu,Minzhi Wei,Sumin Yang,Caoqing Jiang. Bifurcation of Limit Cycles from a Liénard System of Degree 4[J].Acta mathematica scientia,Series A, 2021, 41(4): 936-953.

Trendmd

Figures/Tables 2

References 42

1	Arnold V I . Arnold's Problems. Berlin: Springer-Verlag, 2004
2	Arnold V I . Loss of stability of self-oscillations close to resonance and versal deformations of equivariant vector fields. Funct Anal Appl, 1977, 11, 85- 92 doi: 10.1007/BF01081886
3	Arnold V I . Ten problems. Adv Soviet Math, 1990, 1, 1- 8
4	Chen F D , Li C Z , Llibre J , Zhang Z H . A unified proof on the weak Hilbert 16th problem for $n=2$. J Differ Equations, 2006, 221 (2): 309- 342 doi: 10.1016/j.jde.2005.01.009
5	Chen L , Ma X Z , Zhang G M , Li C Z . Cyclicity of several quadratic reversible systems with center of genus one. J Appl Anal Comput, 2011, 1 (4): 439- 447
6	Christopher C , Li C Z . Limit Cycles of Differential Equations. Basel: Birkhäuser, 2007
7	Dumortier F , Li C Z . Perturbations from an elliptic Hamiltonian of degree four: (Ⅰ) Saddle loop and two saddle cycle. J Differ Equations, 2001, 176, 114- 157 doi: 10.1006/jdeq.2000.3977
8	Dumortier F , Li C Z . Perturbations from an elliptic Hamiltonian of degree four: (Ⅱ) Cuspidal loop. J Differ Equations, 2001, 175, 209- 243 doi: 10.1006/jdeq.2000.3978
9	Dumortier F , Li C Z . Perturbation from an elliptic Hamiltonian of degree four: Ⅲ Global center. J Differ Equations, 2003, 188, 473- 511 doi: 10.1016/S0022-0396(02)00110-9
10	Dumortier F , Li C Z . Perturbations from an elliptic Hamiltonian of degree four: (Ⅳ) Figure eight-loop. J Differ Equations, 2003, 88, 512- 514
11	Écalle J . Introduction Aux Fonctions Analysables et Preuve Constructive De la Conjecture De Dulac. French: Hermann, 1992
12	Gavrilov L . The infinitesimal 16th Hilbert problem in the quadratic case. Invent Math, 2001, 143, 449- 497 doi: 10.1007/PL00005798
13	Grau M , Mañosas F , Villadelprat J . A Chebyshev criterion for Abelian integrals. Trans Amer Math Soc, 2011, 363, 109- 129 doi: 10.1090/S0002-9947-2010-05007-X
14	Han M A . Asymptotic expansions of Melnikov functions and limit cycle bifurcations. Int J Bifur Chaos, 2012, 22, 1250296 doi: 10.1142/S0218127412502963
15	Han M A . Existence of at most 1, 2, or 3 zeros of a melnikov function and limit cycles. J Differ Equations, 2001, 170 (2): 325- 343 doi: 10.1006/jdeq.2000.3828
16	Han M A . On Hopf cyclicity of planar systems. J Math Anal Appl, 2000, 245 (2): 404- 422 doi: 10.1006/jmaa.2000.6758
17	Han M A , Wang Z , Zang H . Limit cycles by Hopf and homoclinic bifurcations for near-Hamiltonian systems. Chinese Ann Math Series A, 2007, 62 (5): 3214- 3234
18	Han M A , Yang J M , Tarta A A , Gao Y . Limit cycles near homoclinic and heteroclinic loops. J Dynam Differ Equat, 2008, 20, 923- 944 doi: 10.1007/s10884-008-9108-3
19	Han M A , Yang J M , Yu P . Hopf bifurcations for near-Hamiltonian systems. Inter J Bifur Chaos, 2009, 19 (12): 4117- 4130 doi: 10.1142/S0218127409025250
20	Hilbert D . Mathematical problems. Bull Amer Math Soc, 1902, 8, 437- 479 doi: 10.1090/S0002-9904-1902-00923-3
21	Horozov E , Iliev I D . On the number of limit cycles in perturbations of quadratic Hamiltonian systems. Proc London Math Soc, 1994, 69, 198- 224
22	Ilyashenko Y S . Finiteness Theorems for Limit Cycles. Providence RI: Amer Math Soc, 1991
23	Li C Z . Abelian integrals and limit cycles. Qual Theory Dyn Syst, 2012, 11, 111- 128 doi: 10.1007/s12346-011-0051-z
24	李承治, 李伟固. 弱化希尔伯特第16问题及其研究现状. 数学进展, 2010, 39 (5): 513- 526 doi: 10.11845/sxjz.2010.39.05.0513
	Li C Z , Li W G . Weak Hilbert's 16th problem and the relative research. Adv Math(CHINA), 2010, 39 (5): 513- 526 doi: 10.11845/sxjz.2010.39.05.0513
25	Li C Z , Zhang Z F . A criterion for determining the monotonicity of the ratio of two abelian integrals. J Differ Equations, 1996, 124, 407- 424 doi: 10.1006/jdeq.1996.0017
26	Li C Z , Zhang Z H . Remarks on 16th weak Hilbert problem for $n = 2$. Nonlinearity, 2002, 15, 1975- 1992 doi: 10.1088/0951-7715/15/6/310
27	Li J B . Hilberts 16th problem and bifurcations of planar polynomial vector fields. Inter J Bifur Chaos, 2003, 13, 47- 106 doi: 10.1142/S0218127403006352
28	Liu C J . The cyclicity of period annuli of a class of quadratic reversible systems with two centers. J Differ Equations, 2012, 252 (10): 5260- 5273 doi: 10.1016/j.jde.2012.02.005
29	Liu C J , Xiao D M . The monotonicity of the ratio of two Abelian integrals. Tran the Ame Math Soc, 2013, 365 (10): 5525- 5544 doi: 10.1090/S0002-9947-2013-05934-X
30	Manosas F , Villadelprat J . Bounding the number of zeros of certain Abelian integrals. J Differ Equations, 2011, 251 (6): 1656- 1669 doi: 10.1016/j.jde.2011.05.026
31	Petrov G S . Number of zeros of complete elliptic integrals. Funct Anal App, 1984, 18 (2): 148- 149 doi: 10.1007/BF01077834
32	Pontryagin L S . On dynamical systems close to hamiltonian ones. Zh Exp Theor Phys, 1934, 4, 234- 238
33	Smale S . Mathematical problems for the next century. Math Intelligencer, 1998, 2, 7- 15
34	Sun X B , Huang W T . Bounding the number of limit cycles for a polynomial Liénard system by using regular chains. J Symb Comput, 2017, 79, 197- 210 doi: 10.1016/j.jsc.2016.02.004
35	Sun X B , Su J , Han M A . On the number of zeros of Abelian integral for some Liénard system of type (4, 3). Chaos Soliton Fract, 2013, 51, 1- 12 doi: 10.1016/j.chaos.2013.02.003
36	孙宪波, 吴奎霖. 一类扰动超椭圆Hamilton系统的Abel积分零点个数上确界. 中国科学, 2015, 45 (6): 751- 764
	Sun X B , Wu K L . The sharp bound on the number of zeros of Abelian integral for a perturbation of hyper-elliptic Hamiltonian system. Science in China, 2015, 45 (6): 751- 764
37	Sun X B , Xi H J , Zangeneh H R Z , Kazemi R . Bifurcation of limit cycles in small perturbation of a class of Liénard systems. Int J Bifur Chaos, 2014, 24 (01): 1450004 doi: 10.1142/S0218127414500047
38	Tian Y , Han M A . Hopf and homoclinic bifurcations for near-Hamiltonian systems. J Differ Equat, 2017, 262 (4): 3214- 3234 doi: 10.1016/j.jde.2016.11.026
39	Wang J H . Estimate of the number of zeros of Abelian integrals for a perturbation of hyperelliptic Hamiltonian system with nilpotent center. Chaos Soliton Fract, 2012, 45, 1140- 1146 doi: 10.1016/j.chaos.2012.05.011
40	Wang J H , Xiao D M . On the number of limit cycles in small perturbations of a class of hyperelliptic Hamiltonian systems with one nilpotent saddle. J Differ Equations, 2011, 250, 2227- 2243 doi: 10.1016/j.jde.2010.11.004
41	Xiao D M . Bifurcations on a five-parameter family of planar vector field. J Dyn Diff Equat, 2008, 20, 961- 980 doi: 10.1007/s10884-008-9109-2
42	Zhang Z F , Li C Z . On the number of limit cycles of a class of quadratic Hamiltonian systems under quadratic perturbations. Adv in Math, 1997, 26, 445- 460

[1]	Jihua Yang,Erli Zhang. Bifurcation of Periodic Orbits of an n-Dimensional Piecewise Smooth Differential System [J]. Acta mathematica scientia,Series A, 2020, 40(4): 1043-1052.
[2]	Kun Zhu,Jianhe Shen. A Revisit on Multiple-Pulse Homoclinic Solutions in a Generalized Gierer-Meinhardt Equation [J]. Acta mathematica scientia,Series A, 2019, 39(6): 1365-1375.
[3]	Gaixia Wang,Jixuan Liu,Xuezhi Li. Stability of Age-Structured with Proportion of Infected Groups or Enter the Latent Epidemiological Model with Varying Population Size [J]. Acta mathematica scientia,Series A, 2019, 39(5): 1260-1271.
[4]	Zhibo Cheng,Zhonghua Bi,Shaowen Yao. Periodic Solution for p-Laplacian Liénard Equation with Attractive Singularity and Time-Dependent Deviating Argument [J]. Acta mathematica scientia,Series A, 2019, 39(2): 277-285.
[5]	Hua Li,Sanhong Liu,Yile Fang,Xingan Zhang. Mathematical Modeling and Computer Simulation on Hand, Foot and Mouth Disease in Children [J]. Acta mathematica scientia,Series A, 2018, 38(5): 1032-1040.
[6]	Liao Shupeng, Shen Jianhe. One-Pulse Travelling Front Solutions of a sine-Gordon Equation with Slowly Varying Parameters [J]. Acta mathematica scientia,Series A, 2018, 38(4): 810-822.
[7]	Liang Haihua, Chen Yuming, Cen Xiuli. Limit Cycles Bifurcating from a Class of Quasi-Homogeneous Polynomial Center [J]. Acta mathematica scientia,Series A, 2018, 38(1): 1-9.
[8]	Fu Jinbo, Chen Lansun. Positive Periodic Solution of Multiple Species Comptition System with Ecological Environment and Feedback Controls [J]. Acta mathematica scientia,Series A, 2017, 37(3): 553-561.
[9]	Jiang Ani. Pseudo Almost Periodic Solutions for a Model of Hematopoiesis with an Oscillating Circulation Loss Rate [J]. Acta mathematica scientia,Series A, 2016, 36(1): 80-89.
[10]	Xu Yanli. Exponential Convergence of An Epidemic Model with Delays and Oscillating Recovery Rates [J]. Acta mathematica scientia,Series A, 2015, 35(5): 987-994.

Bifurcation of Limit Cycles from a Liénard System of Degree 4

RichHTML

PDF (PC)

Abstract

Cite this article

share this article

Figures/Tables 2

References 42

Related Articles 10

Metrics

Comments

Recommended 10