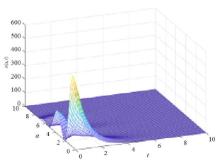
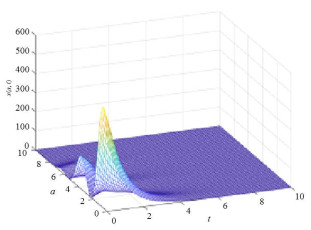
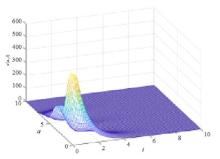
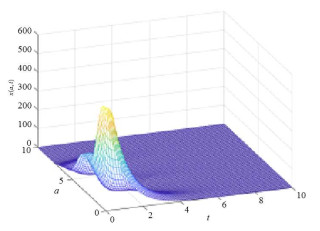
Acta mathematica scientia,Series A ›› 2020, Vol. 40 ›› Issue (6): 1712-1722.
Stability of a Class of Nonlinear Hierarchical Age-Dependent Population Model
Zerong He*( ),Zhiqiang Zhang,Yang Wang
),Zhiqiang Zhang,Yang Wang
- Department of Mathematics, Hangzhou Dianzi University, Hangzhou 310018
-
Received:2019-10-24Online:2020-12-26Published:2020-12-29 -
Contact:Zerong He E-mail:zrhe@hdu.edu.cn
CLC Number:
- O211.4
Cite this article
Zerong He,Zhiqiang Zhang,Yang Wang. Stability of a Class of Nonlinear Hierarchical Age-Dependent Population Model[J].Acta mathematica scientia,Series A, 2020, 40(6): 1712-1722.
share this article
| 1 |
Gurtin M E , MacCamy R C . Non-linear age-dependent population dynamics. Arch Rational Mech Anal, 1974, 54 (3): 281- 300
doi: 10.1007/BF00250793 |
| 2 |
Prüss J . On the qualitative behaviour of populations with age-specific interactions. Computers & Mathematics with Applications, 1983, 9 (3): 327- 339
doi: 10.1016/0898-1221(83)90020-2 |
| 3 | Gyllenberg M . Stability of nonlinear age-dependent population model containing a control variable. SIAM J Appl Math, 1983, 43 (6): 1418- 1438 |
| 4 | Li J . Dynamics of age-structured predator-prey population models. J Math Anal Appl, 1990, 152: 399- 415 |
| 5 | Li X . The stability of nonlinear age-dependent population equation. Appl Math Lett, 1998, 11 (6): 19- 26 |
| 6 | Kamioka K. Mathematical analysis of an age-structured population model with space-limited recruitment. 2005, 198: 27-56 |
| 7 | Iannelli M, Milner F. The Basic Approach to Age-Structured Population Dynamics: Models, Methods and Numerics. Dordrecht: Springer, 2017 |
| 8 |
Diekmann O , Heijmans H J A M , Thieme H R . On the stability of the cell size distribution. J Math Biology, 1984, 19: 227- 248
doi: 10.1007/BF00277748 |
| 9 |
Farkas J Z . Stability conditions for a non-linear size-structured model. Nonlinear Analysis:Real World Apllications, 2005, 6: 962- 969
doi: 10.1016/j.nonrwa.2004.06.003 |
| 10 |
Liu Y , He Z R . Stability results for a size-structured population model with resources-dependence and inflow. J Math Anal Appl, 2009, 360: 665- 675
doi: 10.1016/j.jmaa.2009.07.005 |
| 11 | 何泽荣, 杨立志. 具有尺度结构和双加权的种群模型:稳定性与最优收获. 数学物理学报, 2016, 36A (3): 584- 600 |
| He Z , Yang L . A weighted population model with size-structure:Stability and optimal harvesting. Acta Mathematica Scientia, 2016, 36A (3): 584- 600 | |
| 12 |
Farkas J Z , Hinow P . Steady states in hierarchical structured populations with distributed states at burth. Discrete and Continuous Dyanmical Systems, 2012, 17 (8): 2671- 2689
doi: 10.3934/dcdsb.2012.17.2671 |
| 13 |
He Z R , Chen H , Wang S P . The global dynamics of a discrete nonlinear hierarchical population system. International Journal of Biomathematics, 2019, 12 (2): 1950022
doi: 10.1142/S1793524519500220 |
| 14 | 何泽荣, 张智强, 王淑平. 一类非线性等级结构种群控制模型解的适定性. 系统科学与数学, 2019, 39 (8): 1201- 1211 |
| He Z , Zhang Z Q , Wang S P . The well-posedness of a nonlinear age-structured population control model. J Sys Sci & Math Scis, 2019, 39 (8): 1201- 1211 | |
| 15 | 何泽荣, 张智强, 裘哲勇. 一类非线性等级结构种群模型的数值解法. 数学物理学报, 2020, 40A (2): 515- 526 |
| He Z , Zhang Z , Qiu Z . Numerical method od a nonlinear hierarchical age-structured population model. Acta Mathematica Scientia, 2020, 40A (2): 515- 526 | |
| 16 | Yosida K. Functional Analysis. Berlin: Springer-Verlag, 1980 |
| [1] | Li Xiling, Gao Fei, Li Wenqin. Stability Analysis of Fractional-Order Hepatitis B Virus Infection Model With Immune Delay [J]. Acta mathematica scientia,Series A, 2021, 41(2): 562-576. |
| [2] | Gaihui Guo,Xiaohui Liu. Hopf Bifurcation and Stability for an Autocatalytic Reversible Biochemical Reaction Model [J]. Acta mathematica scientia,Series A, 2021, 41(1): 166-177. |
| [3] | Dandan Du,Yucan Zhu. Stabilities of K- Frames and Tight K- Frames Under the Operator Perturbation [J]. Acta mathematica scientia,Series A, 2021, 41(1): 29-38. |
| [4] | Wei Li,Pengzhan Huang. A Viscosity-Splitting Finite Element Method for the Fluid-Fluid Interaction Problem [J]. Acta mathematica scientia,Series A, 2020, 40(5): 1362-1380. |
| [5] | Yonghui Zhou. Global Stability of the Nonmonotone Critical Traveling Waves for Reaction Diffusion Equations [J]. Acta mathematica scientia,Series A, 2020, 40(4): 983-992. |
| [6] | Jian Liu,Zhixin Zhang,Wei Jiang. Global Mittag-Leffler Stability of Fractional Order Nonlinear Impulsive Differential Systems with Time Delay [J]. Acta mathematica scientia,Series A, 2020, 40(4): 1053-1060. |
| [7] | Xingshou Huang,Ricai Luo,Wusheng Wang. Stability Analysis for a Class Neural Network with Proportional Delay Based on the Gronwall Integral Inequality [J]. Acta mathematica scientia,Series A, 2020, 40(3): 824-832. |
| [8] | Chun Wang,Tianzhou Xu. Hyers-Ulam-Rassias Stability of a Mixed Type Cubic-Quartic Functional Equation in 2-Banach Spaces [J]. Acta mathematica scientia,Series A, 2020, 40(2): 352-368. |
| [9] | Menglan Liao,Bin Guo. Asymptotic Stability of Weak Solutions to Wave Equation with Variable Exponents and Strong Damping Term [J]. Acta mathematica scientia,Series A, 2020, 40(1): 146-155. |
| [10] | Ru Wang,Zhonghua Zhang,Yeling Liu. Dynamical Properties of a Discontinuous Models with Signal Molecules Regulation [J]. Acta mathematica scientia,Series A, 2019, 39(6): 1545-1554. |
| [11] | Xiaojie Jing, Aimin Zhao, Guirong Liu. Global Stability of a Measles Epidemic Model with Partial Immunity and Environmental Transmission [J]. Acta mathematica scientia,Series A, 2019, 39(4): 909-917. |
| [12] | Changxu Shao,Shutang Liu. Fractal Feature and Control of Three-Species Predator-Prey Model [J]. Acta mathematica scientia,Series A, 2019, 39(4): 951-962. |
| [13] | Chao Yang,Runjie Li. Existence and Stability of Periodic Solution for a Lasota-Wazewska Model with Discontinuous Harvesting [J]. Acta mathematica scientia,Series A, 2019, 39(4): 785-796. |
| [14] | Qinghua Zhou,Li Wan,Jie Liu. Global Attracting Set for Neutral Type Hopfield Neural Networks with Time-Varying Delays [J]. Acta mathematica scientia,Series A, 2019, 39(4): 823-831. |
| [15] | Yanhua Shi,Yadong Zhang,Fenling Wang,Yanmin Zhao,Pingli Wang. High Accuracy Analysis of Linear Triangular Element for Time Fractional Diffusion Equations [J]. Acta mathematica scientia,Series A, 2019, 39(4): 839-850. |
|