Acta mathematica scientia,Series A ›› 2019, Vol. 39 ›› Issue (6): 1365-1375.
Previous Articles Next Articles
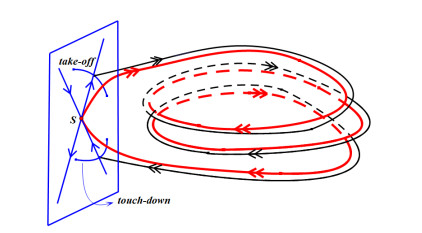
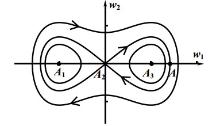
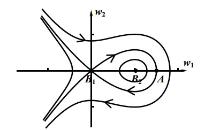
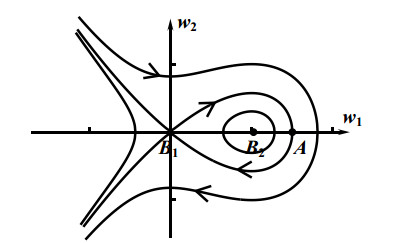
A Revisit on Multiple-Pulse Homoclinic Solutions in a Generalized Gierer-Meinhardt Equation
- 1 College of Mathematics and Informatics, Fujian Normal University, Fuzhou 350117
2 Fujian Key Laboratory of Mathematical Analysis and Applications, Fujian Normal University, Fuzhou 350117
CLC Number:
- O175.12