两类Kampé de Fériet,级数的简化和求和公式

Abstract

Abstract:

Two $_3F_2[1]$ -summation theorems are employed to establish two general transformation formulas for double infinite series. With the help of some classical hypergeometric series summation formulas, the two transformations yield a number of summation formulas for Kampé de Fériet series of type $F_{q:1;0}^{p:2;1}$ . Furthermore a list of reduction and transformation formulas for Kampé de Fériet series of type $F_{q:1;1}^{p:2;2}$ are derived by utilizing four Saalschützian $_4F_3[1]$ -summation formulas.

Key words: hypergeometric series, Kampé de Fériet series, reduction and summation formulas

CLC Number:

O174.6

Liu Hongmei, Li Yang. Reduction and Summation Formulas for Two Types of Kampé de Fériet Series[J].Acta mathematica scientia,Series A, 2025, 45(1): 136-152.

Trendmd

References 36

[1]	Appell P, Kampé de Fériet J. Fonctions Hypergéométriques et Hypersphériques Polynomes D'Hermite. Paris: Gauthier-Villars, 1926
[2]	Bailey W N. Generalized Hypergeometric Series, Cambridge Tracts in Mathematics and Mathematical Physics 32. London: Cambridge University Press, 1935
[3]	Bezrodnykh S I. Analytic continuation of Lauricella's function 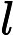$F_D^{(N)}$ for large in modulo variables near hyperplanes $\{z_j=z_l\}$ . Integral Transforms Spec Funct, 2022, 33(4): 276-291
[4]	Bezrodnykh S I. Analytic continuation of Lauricella's function 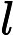$F_D^{(N)}$ for variables close to unit near hyperplanes $\{z_j=z_l\}$ . Integral Transforms Spec Funct, 2022, 33(5): 419-433
[5]	Bezrodnykh S I. Analytic continuation of the Kampé de Fériet function and the general double Horn series. Integral Transforms Spec Funct, 2022, 33(11): 908-928
[6]	Buschman R G, Srivastava H M. Series identities and reducibility of Kampé de Fériet functions. Math Proc Cambridge Philos Soc, 1982, 91(3): 435-440
[7]	Bytev V V, Kniehl B A. Derivatives of any Horn-type hypergeometric functions with respect to their parameters. Nuclear Phys B, 2020, 952: 114911
[8]	Carlitz L. Summation of a special $_4F_3$ . Boll Unione Mat Ital, 1963, 18: 90-93
[9]	Chan W C C, Chen K Y, Chyan C J, Srivastava H M. Some multiple hypergeometric transformations and associated reduction formulas. J Math Anal Appl, 2004, 294(2): 418-437
[10]	Chen K Y, Srivastava H M. Series identities and associated families of generating functions. J Math Anal Appl, 2005, 311(2): 582-599
[11]	Chu W C, Li N N. Reduction and summation formulae for semi-terminating $q$ -Kampé de Fériet series. Afrika Matematika, 2013, 24(4): 647-664
[12]	Chu W C, Srivastava H M. Ordinary and basic bivariate hypergeometric transformations associated with the Appell and Kampé de Fériet functions. J Comput Appl Math, 2003, 156(2): 355-370
[13]	Chu W C, Zhang W L. Well-posed reduction formulas for the $q$ -Kampé de Fériet function. Ukrainian Math J, 2011, 62(11): 1783-1802
[14]	Cvijović D, Miller A R. A reduction formula for the Kampé de Fériet function. Appl Math Lett, 2010, 23(7): 769-771
[15]	Gasper G. Positive integrals of Bessel functions. SIAM J Math Anal, 1975, 6(5): 868-881
[16]	Jia C Z, Wang T M. Reduction and transformation formulae for bivariate basic hypergeometric series. J Math Anal Appl, 2007, 328(2): 1152-1160
[17]	Jia C Z, Wang T M. Transformation and reduction formulae for double 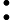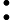$q$ -Clausen series of type $\Phi_{1:1;\mu}^{1:2;\lambda}$ . J Math Anal Appl, 2007, 328(1): 609-624
[18]	Kampé de Fériet J. Les fonctions hypergéométriques d'ordre supérieur à deux variables. CR Acad Sci Paris, 1921, 173: 401-404
[19]	Karlsson P W. Some reducible generalized Kampé de Fériet functions. J Math Anal Appl, 1983, 96(2): 546-550
[20]	Karlsson P W. Some reduction formulae for double power series and Kampé de Fériet functions. Indag Math, 1984, 87(1): 31-36
[21]	Li N N, Chu W. Terminating balanced $_4F_3$ -series and very well-poised $_7F_6$ -series. Ramanujan J, 2019, 49: 465-482
[22]	Liu H M. Hypergeometric series summations and $\pi$ -formulas. J Math Anal Appl, 2014, 419(1): 553-561
[23]	Liu H M, Wang W P. Transformation and summation formulae for Kampé de Fériet series. J Math Anal Appl, 2014, 409(1): 100-110
[24]	刘红梅, 周文书, 李阳. 双变量超几何级数的变换与简化公式. 数学物理学报, 2016, 36A(1): 150-156
	Liu H M, Zhou W S, Li Y. Transformation and reduction formulae for bivariate hypergeometric series. Acta Math Sci, 2016, 36A(1): 150-156
[25]	Luo M J, Raina R K. On certain results related to the hypergeometric function 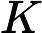$F_K$ . J Math Anal Appl, 2021, 504(2): 125439
[26]	Mouayn Z, Chhaiba H, Kassogue H, Kikodio P K. Husimi Q-functions attached to hyperbolic Landau levels. Rep Math Phys, 2022, 89(1): 27-57
[27]	Pitre S N, Van der Jeugt J. Transformation and summation formulas for Kampé de Fériet series 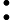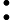$F_{1:1}^{0:3}(1,1)$ . J Math Anal Appl, 1996, 202(1): 121-132
[28]	Santander J L G. A note on some reduction formulas for the generalized hypergeometric function $_2F_2$ and Kampé de Fériet function. Results Math, 2017, 71: 949-954
[29]	Slater L J. Generalized Hypergeometric Functions. Cambridge: Cambridge Univ Press, 1966
[30]	Rao K S, Van der Jeugt J. Stretched 9- $j$ coefficients and summation theorems. J Phys A: Math Gen, 1994, 27(9): 3083-3090
[31]	Srivastava H M, Daoust M C. A note on the convergence of Kampé de Fériet's double hypergeometric series. Math Nachr, 1972, 53(1/6): 151-159
[32]	Srivastava H M, Karlsson P W. Multiple Gaussian Hypergeometric Series. Chichester: Ellis Horwood, 1985
[33]	Srivastava H M, Panda R. An integral representation for the product of two Jacobi polynomials. J Lond Math Soc, 1976, 2(4): 419-425
[34]	Van der Jeugt J.Transformation formula for a double Clausenian hypergeometric series, its $q$ -analogue, and its invariance group. J Comput Appl Math, 2002, 139(1): 65-73
[35]	Van der Jeugt J, Pitre S N, Rao K S. Transformation and summation formulas for double hypergeometric series. J Comput Appl Math, 1997, 83(2): 185-193
[36]	Zhang W L. New transformation and reduction formulae for double $q$ -Clausen series. J Math Anal Appl, 2013, 402(2): 710-718

Metrics

Viewed

Full text

158

HTML			PDF

Just accepted	Online first	Issue	Just accepted	Online first	Issue
0	0	0	0	0	158

From	Others	local

Times	1	157
Rate	1%	99%

Abstract

Just accepted	Online first	Issue

0	0	39

From	Others	local

Times	38	1
Rate	97%	3%

Cited

Web of Science	Crossref	ScienceDirect	Search for Citations in Google Scholar >>


This page requires you have already subscribed to WoS.

Shared

Discussed

Reduction and Summation Formulas for Two Types of Kampé de Fériet Series

RichHTML

PDF (PC)

Abstract

Cite this article

share this article

References 36

Related Articles 3

Metrics

Comments

Recommended 10

[1]	Hongmei Liu. Infinite Series Involving Central Binomial Coefficients and Generalized Harmonic Numbers [J]. Acta mathematica scientia,Series A, 2020, 40(3): 631-640.
[2]	Liu Hongmei, Zhou Wenshu, Li Yang. Transformation and Reduction Formulae for Bivariate Hypergeometric Series [J]. Acta mathematica scientia,Series A, 2016, 36(1): 150-156.
[3]	ZHANG Chun-Gou. The Second Moments for Meyer Konig and Zeller Operators on a Simplex [J]. Acta mathematica scientia,Series A, 2005, 25(2): 256-263.