Acta mathematica scientia,Series A ›› 2024, Vol. 44 ›› Issue (5): 1368-1379.
Previous Articles Next Articles
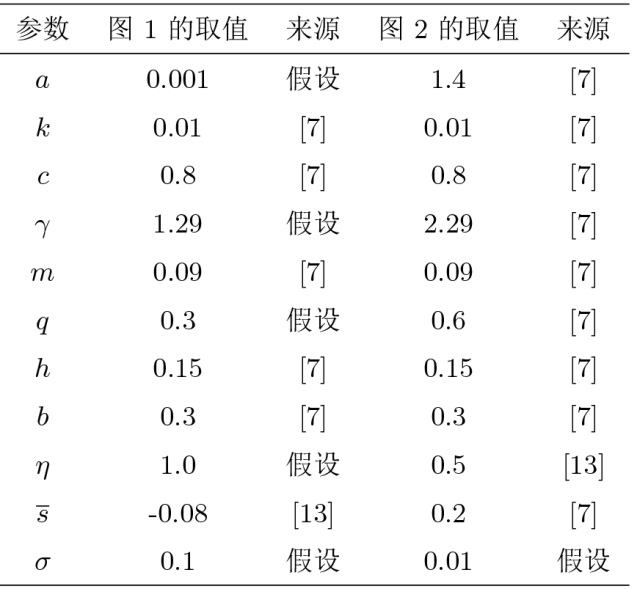
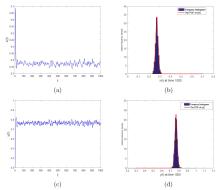
Exponential Extinction, Stationary Distribution and Probability Density Function of A Stochastic Predator-Prey Model with Ornstein-Uhlenbeck Process
Zhang Wenwen,Liu Zhijun*( ),Wang Qinglong
),Wang Qinglong
- School of Mathematics and Statistics, Hubei Minzu University, Hubei Enshi 445000
-
Received:2023-10-30Revised:2024-04-15Online:2024-10-26Published:2024-10-16 -
Supported by:National Natural Science Foundation of China(12101211);Natural Science Foundation of Hubei Province of China(2023AFB1095)
CLC Number:
- O175
Cite this article
Zhang Wenwen, Liu Zhijun, Wang Qinglong. Exponential Extinction, Stationary Distribution and Probability Density Function of A Stochastic Predator-Prey Model with Ornstein-Uhlenbeck Process[J].Acta mathematica scientia,Series A, 2024, 44(5): 1368-1379.
share this article
| [1] | 马知恩. 种群生态学的数学建模与研究. 合肥: 安徽教育出版社, 1996 |
| Ma Z E. Mathematical Modeling and Research of Population Ecology. Hefei: Anhui Education Press, 1996 | |
| [2] |
Su W, Zhang X. Global stability and canard explosions of the predator-prey model with the sigmoid functional response. SIAM J Appl Math, 2022, 82(3): 976-1000
doi: 10.1137/21M1437755 |
| [3] | Santra P K, Mahapatra G S, Phaijoo G R. Bifurcation and chaos of a discrete predator-prey model with Crowley-Martin functional response incorporating proportional prey refuge. Math Probl Eng, 2020, 2020: 1-18 |
| [4] | Zhou Y, Sun W, Song Y F, et al. Hopf bifurcation analysis of a predator-prey model with Holling-II type functional response and a prey refuge. Nonlinear Dyn, 2019, 97: 1439-1450 |
| [5] | Sarkar K, Khajanchi S. Impact of fear effect on the growth of prey in a predator-prey interaction model. Ecol Complex, 2020, 42: 100826 |
| [6] | Liu Y Y, Cao Q, Yang W S. Influence of Allee effect and delay on dynamical behaviors of a predator-prey system. Comput Appl Math, 2022, 41(8): 396 |
| [7] | Mishra S, Upadhyay R K. Spatial pattern formation and delay induced destabilization in predator-prey model with fear effect. Math Method Appl Sci, 2022, 11: 45 |
| [8] | May R M. Stability and Complexity in Model Ecosystems. New Jersey: Princeton University Press, 2001 |
| [9] | Chen X Z, Tian B D, Xu X, et al. A stochastic predator-prey system with modified LG-Holling type II functional response. Math Comput Simul, 2023, 203: 449-485 |
| [10] | Tian B D, Yang L, Chen X Z, et al. A generalized stochastic competitive system with Ornstein-Uhlenbeck process. Int J Biomath, 2021, 14(1): 2150001 |
| [11] | Zhang X H, Yang Q, Jiang D Q. A stochastic predator-prey model with Ornstein-Uhlenbeck process: Characterization of stationary distribution, extinction and probability density function. Commun Nonlinear Sci Numer Simul, 2023, 122: 107259 |
| [12] | Mu X J, Jiang D Q, Hayat T, et al. A stochastic turbidostat model with Ornstein-Uhlenbeck process: Dynamics analysis and numerical simulations. Nonlinear Dyn, 2022, 107(3): 2805-2817 |
| [13] | Zhou B Q, Jiang D Q, Hayat T. Analysis of a stochastic population model with mean-reverting Ornstein-Uhlenbeck process and Allee effects. Commun Nonlinear Sci Numer Simul, 2022, 111: 106450 |
| [14] | Yang Q, Zhang X H, Jiang D Q. Dynamical behaviors of a stochastic food chain system with Ornstein-Uhlenbeck process. J Nonlinear Sci, 2022, 32(3): 34 |
| [15] | Shi Z F, Jiang D Q. Environmental variability in a stochastic HIV infection model. Commun Nonlinear Sci Numer Simul, 2023, 120: 107201 |
| [16] | Zuo W J, Jiang D Q. Stationary distribution and periodic solution for stochastic predator-prey systems with nonlinear predator harvesting. Commun Nonlinear Sci Numer Simul, 2016, 36: 65-80 |
| [17] | Allen E. Environmental variability and mean-reverting processes. Discrete Contin Dyn Syst Ser B, 2016, 21(7): 2073-2089 |
| [18] | Kutoyants Y A. Statistical Inference for Ergodic Diffusion Processes. London: Springer, 2003 |
| [19] | Khasminskii R. Stochastic Stability of Differential Equations. New York: Springer Science Business Media, 2011 |
| [20] | Gardiner C W. Handbook of Stochastic Methods for Physics, Chemistry and the Natural Sciences. Berlin: Springer, 1985 |
| [21] | Oksendal B. Stochastic Differential Equations:An Introduction with Applications. New York: Springer-Verlag Heidelberg, 2000 |
| [22] | Ma Z E, Zhou Y C, Li C Z. Qualitative and Stability Methods for Ordinary Differential Equations. Beijing: Science Press, 2015 |
| [23] | 何晓群. 多元统计分析. 北京: 中国人民大学出版社, 2019 |
| He X Q. Multivariate Statistical Analysis. Beijing: China Renmin University Press, 2019 |
| [1] | Wang Qiufen, Zhang Shuwen. Stochastic Predator-Prey System with Fear Effect and Holling-Type III Functional Response [J]. Acta mathematica scientia,Series A, 2024, 44(5): 1380-1391. |
| [2] |
Chen Yong,Li Ying,Sheng Ying,Gu Xiangmeng.
Parameter Estimation for an Ornstein-Uhlenbeck Process Driven by a Type of Gaussian Noise with Hurst Parameter |
| [3] | Li Dan,Wei Fengying,Mao Xuerong. Survival Analysis of an SVIR Epidemic Model with Media Coverage [J]. Acta mathematica scientia,Series A, 2023, 43(5): 1595-1606. |
| [4] | Chen Yong,Gu Xiangmeng. An Improved Berry-Esséen Bound of Least Squares Estimation for Fractional Ornstein-Uhlenbeck Processes [J]. Acta mathematica scientia,Series A, 2023, 43(3): 855-882. |
| [5] | Huang ,Liu Haiyan,Chen Mi. Proportional Reinsurance and Investment Based on the Ornstein-Uhlenbeck Process in the Presence of Two Reinsurers [J]. Acta mathematica scientia,Series A, 2023, 43(3): 957-969. |
| [6] | Bo Li,Ziwei Liang. Stability of Stage-Structured Predator-Prey Models with Beddington-DeAngelis Functional Response [J]. Acta mathematica scientia,Series A, 2022, 42(6): 1826-1835. |
| [7] | Tong Zhao,Hailong Yuan,Gaihui Guo. Positive Solutions of a Predator-Prey Model with Modified Leslie-Gower Type [J]. Acta mathematica scientia,Series A, 2022, 42(1): 176-186. |
| [8] | Jiang Li,Guijie Lan,Shuwen Zhang,Chunjin Wei. Dynamics Analysis of a Stochastic Glucose-Insulin Model [J]. Acta mathematica scientia,Series A, 2021, 41(6): 1937-1949. |
| [9] | Liya Liu,Daqing Jiang. Global Dynamics of a Stochastic Chemostat Model with General Response Function and Wall Growth [J]. Acta mathematica scientia,Series A, 2021, 41(6): 1912-1924. |
| [10] | Tengfei Wang,Tao Feng,Xinzhu Meng. Complex Dynamics and Stochastic Sensitivity Analysis of a Predator-Prey Model with Crowley-Martin Type Functional Response [J]. Acta mathematica scientia,Series A, 2021, 41(4): 1192-1203. |
| [11] | Tingting Jiang,Zengji Du. Periodic Solutions of a Neutral Impulsive Predator-Prey Model with Holling-Type IV Functional Response [J]. Acta mathematica scientia,Series A, 2021, 41(1): 178-193. |
| [12] | Changxu Shao,Shutang Liu. Fractal Feature and Control of Three-Species Predator-Prey Model [J]. Acta mathematica scientia,Series A, 2019, 39(4): 951-962. |
| [13] | Guijie Lan,Yingjie Fu,Chunjin Wei,Shuwen Zhang. Stationary Distribution and Periodic Solution for Stochastic Predator-Prey Systems with Holling-Type Ⅲ Functional Response [J]. Acta mathematica scientia,Series A, 2018, 38(5): 984-1000. |
| [14] | Wei Fengying, Lin Qingteng. Extinction and Distribution for an SIQS Epidemic Model with Quarantined-Adjusted Incidence [J]. Acta mathematica scientia,Series A, 2017, 37(6): 1148-1161. |
| [15] | Zhang Shuwen. A Stochastic Predator-Prey System with Time Delays and Prey Dispersal [J]. Acta mathematica scientia,Series A, 2015, 35(3): 592-603. |
| Viewed | ||||||||||||||||||||||||||||||||||||||||||||||
|
Full text 141
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Abstract 52
|
|
|||||||||||||||||||||||||||||||||||||||||||||
Cited |
|
|||||||||||||||||||||||||||||||||||||||||||||
| Shared | ||||||||||||||||||||||||||||||||||||||||||||||
| Discussed | ||||||||||||||||||||||||||||||||||||||||||||||
|