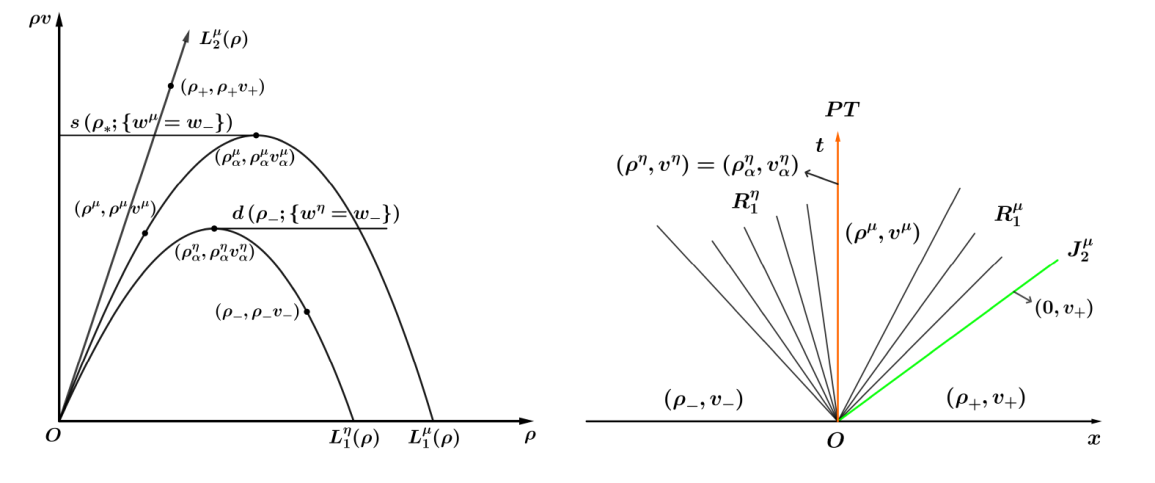
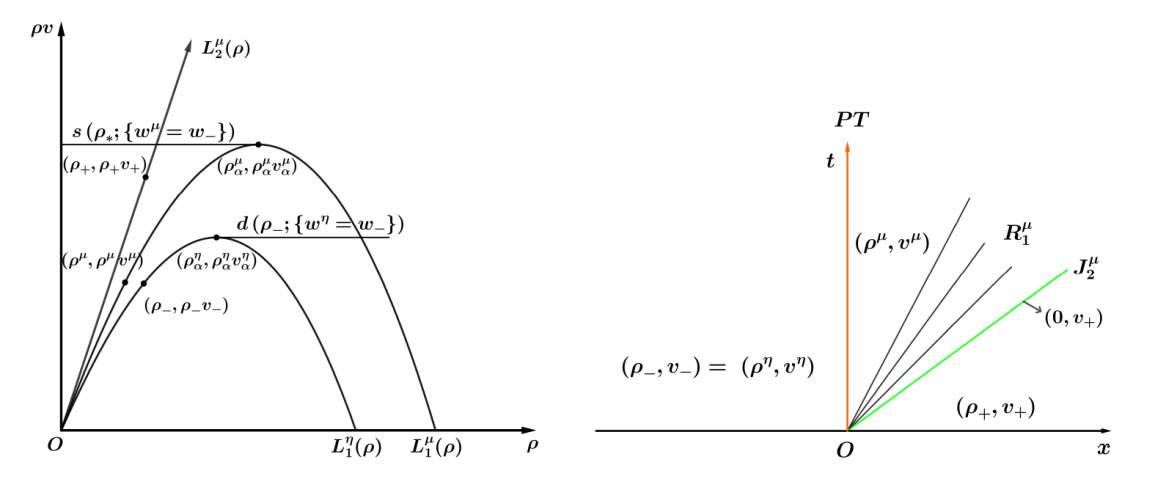
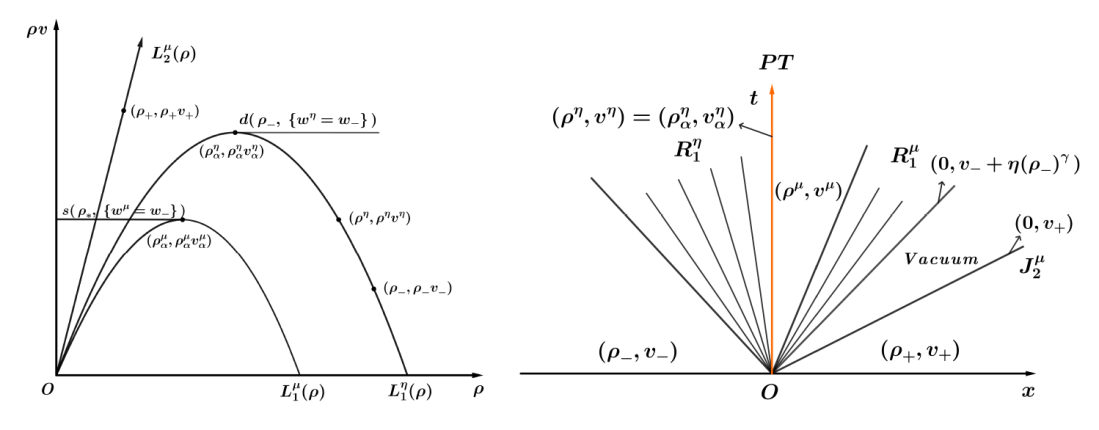
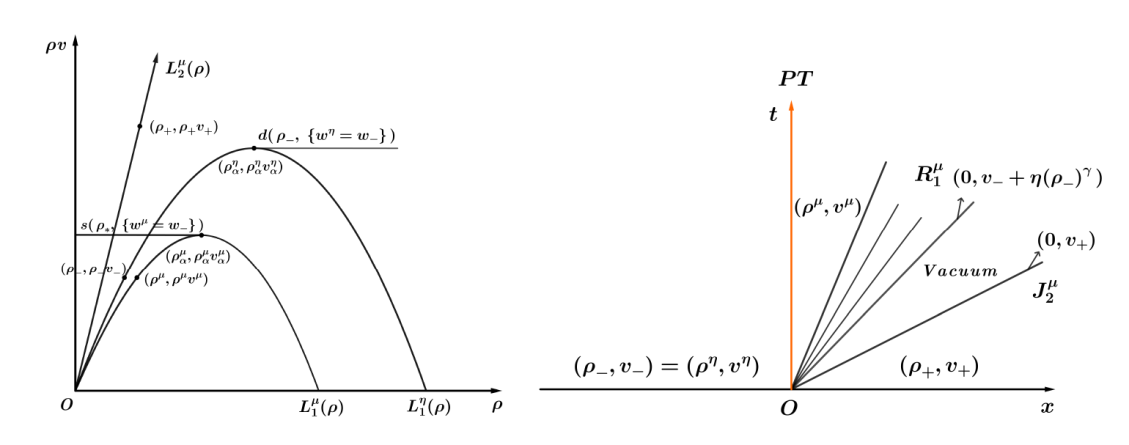
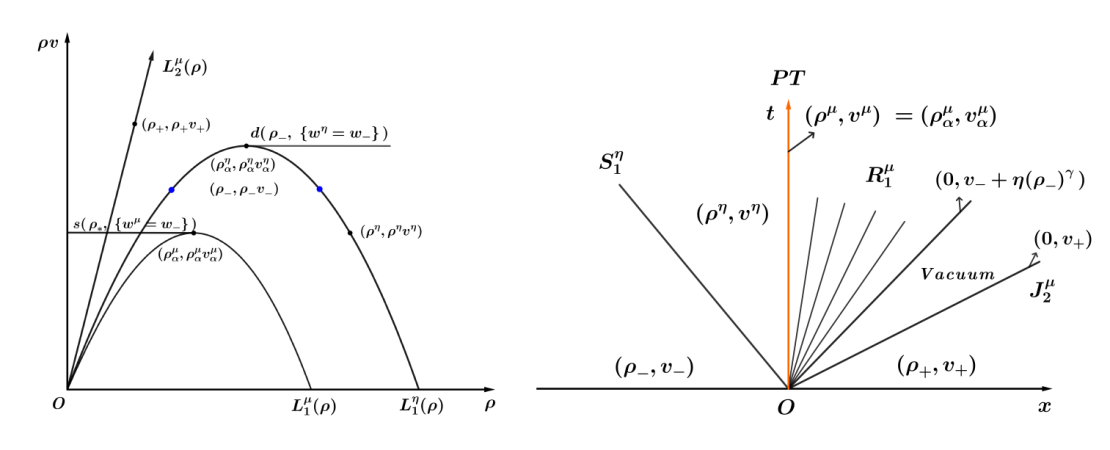
| [1] |
Aw A, Rascle M. Resurrection of second order models of traffic flow. SIAM Journal on Applied Mathematics, 2000, 60(3): 916-938
|
| [2] |
Colombo R M, Goatin P, Piccoli B. Road networks with phase transitions. Journal of Hyperbolic Differential Equations, 2010, 7(1): 85-106
|
| [3] |
Goatin P. The Aw-Rascle vehicular traffic flow model with phase transitions. Mathematical and Computer Modelling, 2006, 44(3/4): 287-303
|
| [4] |
Gttlich S, Herty M, Moutari S, et al. Second-Order traffic flow models on networks. SIAM Journal on Applied Mathematics, 2021, 81(1): 258-281
|
| [5] |
Herty M, Schleper V. Traffic flow with unobservant drivers. ZAMM Journal of Applied Mathematics and Mechanics: Ztschrift Fur Angewandte Mathematik und Mechanik, 2011, 91(10): 763-776
|
| [6] |
Holden H, Risebro N H. A Mathematical model of traffic flow on a network of unidirectional roads. Siam Journal on Mathematical Analysis, 1995, 26(4): 999-1017
|
| [7] |
Jiang W F, Wang Z. Developing an Aw-Rascle model of traffic flow. Journal of Engineering Mathematics, 2016, 97(1): 135-146
|
| [8] |
Moutari S, Herty M, Klein A, et al. Modelling road traffic accidents using macroscopic second-order models of traffic flow. Ima Journal of Applied Mathematics, 2013, 78(5): 1087-1108
|
| [9] |
王文雷. 针对耦合的 AR 交通模型 Riemann 问题的研究. 江苏: 南京航空航天大学, 2021
|
|
Wang W L. Study on the Riemann of Coupling AR model. Jiangsu: Nanjing University of Aeronautics and Astronautics, 2021
|
| [10] |
Zhang H M. A non-equilibrium traffic model devoid of gas-like behavior. Transportation Research Part B: Methodological, 2002, 36(3): 275-290
|
 ),Lv Shun(
),Lv Shun( ),Weng Shasha(
),Weng Shasha( )
)