具有捕获项的 Beddington-DeAnglis 型捕食-食饵扩散模型的动力学分析

Abstract

Abstract:

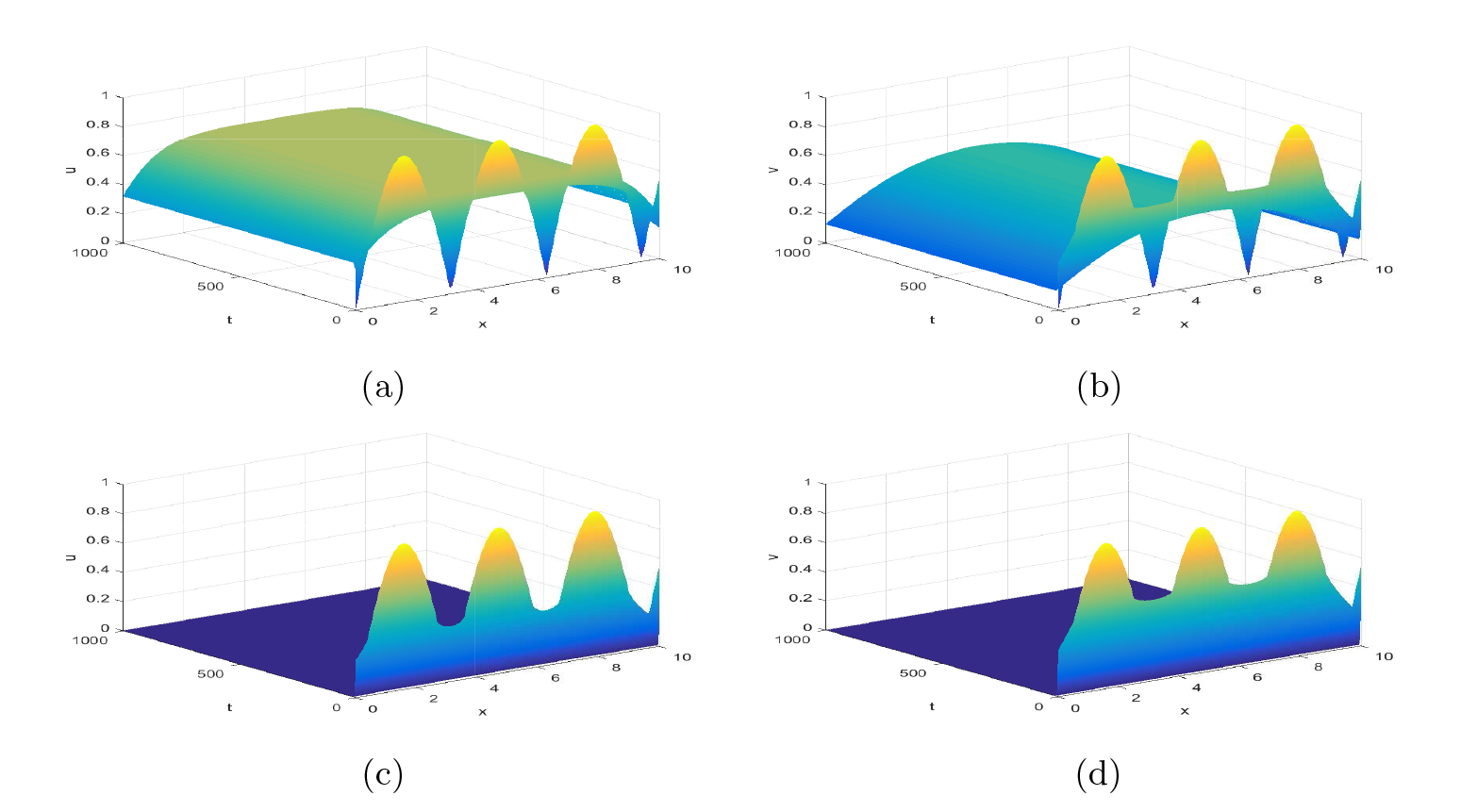
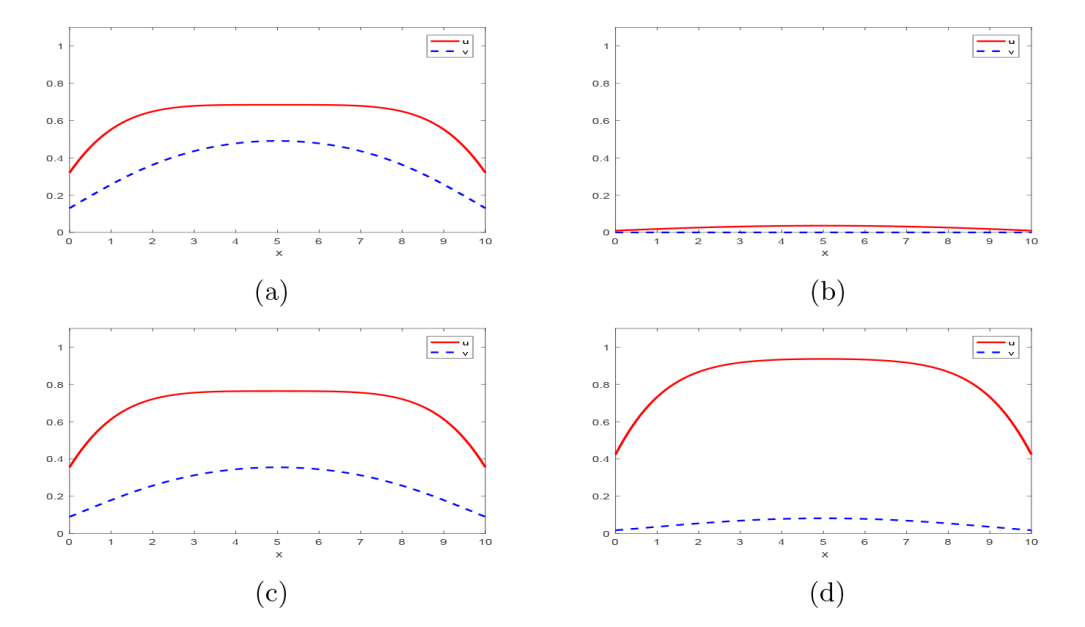
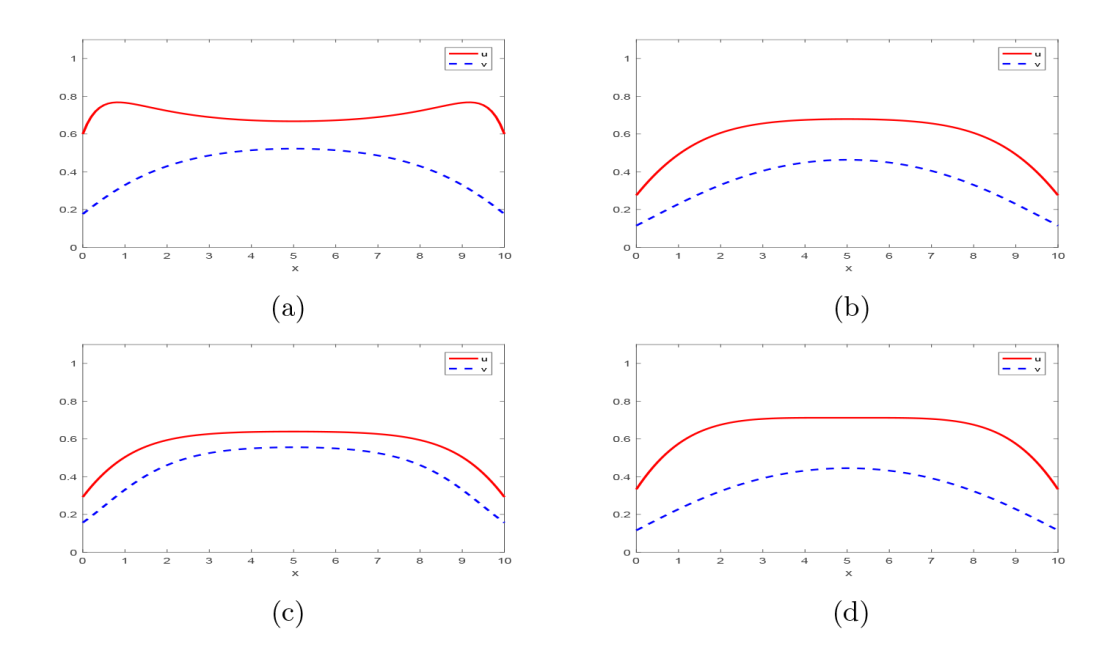
A diffusive predator-prey model with Beddington-DeAngelis function response and harvesting is studied. Firstly, the sufficient conditions for the existence of positive solutions are obtained by the fixed point index theory, and the multiplicity of positive solutions is discussed by the bifurcation theorem. Then, by virtue of the combination of the perturbation theory for linear operators, degree theory and stability theory, the uniqueness and stability of positive solution are investigated when the interaction among predators is large. In addition, we analyze the extinction and permanence of the two species by means of the comparison principle of parabolic systems. Finally, we make some numerical simulations to validate and complement the theoretical results. If the maximal growth rate of the prey is large and low density mortality of the predator is small, the findings suggest that the model has only one unique asymptotically stable positive solution provided that the effect of the interaction among predators is sufficiently large and the harvesting rate of the predator lies in a certain range; and has at least two positive solutions when the harvesting rate of the predator belongs to another range.

Key words: Harvesting, Nonconstant mortality rate, Uniqueness, Stability, Multiplicity

CLC Number:

O175.26

Fan Shishi, Li Haixia, Lu Yindou. Dynamics Analysis of a Diffusive Predator-Prey Model with Beddington-DeAngelis Function Response and Harvesting[J].Acta mathematica scientia,Series A, 2023, 43(6): 1929-1942.

Trendmd

Figures/Tables 5

References 22

[1]	Ko W, Ryu K. Qualitative analysis of a predator-prey model with Holling type II functional response incorporating a prey refuge. J Differential Equations, 2006, 231(2): 534-550 doi: 10.1016/j.jde.2006.08.001
[2]	Peng R, Shi J. Non-existence of non-constant positive steady states of two Holling type-II predator-prey systems: Strong interaction case. J Differential Equations, 2009, 247(3): 866-886 doi: 10.1016/j.jde.2009.03.008
[3]	Lu M, Huang J. Global analysis in Bazykin's model with Holling II functional response and predator competition. J Differential Equations, 2021, 280: 99-138 doi: 10.1016/j.jde.2021.01.025
[4]	Chen W Y, Wang M X. Qualitative analysis of predator-prey models with Beddington-DeAngelis functional response and diffusion. Math Comput Model, 2005, 42(1): 31-44 doi: 10.1016/j.mcm.2005.05.013
[5]	Zhao S. Analysis on stochastic dynamics of two-consumers-one-resource competing systems with Beddington-DeAngelis functional response. Int J Biomath, 2021, 14(2): 2050058 doi: 10.1142/S1793524520500588
[6]	Wang R, Jia Y F. Analysis on bifurcation for a predator-prey model with Beddington-DeAngelis functional response and non-selective harvesting. Acta Appl Math, 2016, 143: 15-27 doi: 10.1007/s10440-015-0025-2
[7]	Liu X, Huang Q. The dynamics of a harvested predator-prey system with Holling type IV functional response. Biosystems, 2018, 169: 26-39
[8]	Liu X, Huang Q. Analysis of optimal harvesting of a predator-prey model with Holling type IV functional response. Ecol Complex, 2020, 42: 100816 doi: 10.1016/j.ecocom.2020.100816
[9]	Djilali S, Bentout S. Pattern formations of a delayed diffusive predator-prey model with predator harvesting and prey social behavior. Math Method Appl Sci, 2021, 44(11): 9128-9142 doi: 10.1002/mma.v44.11
[10]	Duque C, Lizana M. On the dynamics of a predator-prey model with nonconstant death rate and diffusion. Nonlinear Anal: RWA, 2011, 12(4): 2198-2210 doi: 10.1016/j.nonrwa.2011.01.002
[11]	Yang R, Wei J. Bifurcation analysis of a diffusive predator-prey system with nonconstant death rate and Holling III functional response. Chaos Soliton Fract, 2015, 70: 1-13 doi: 10.1016/j.chaos.2014.10.011
[12]	Peng H, Zhang X. The dynamics of stochastic predator-prey models with non-constant mortality rate and general nonlinear functional response. J Nonl Mod Anal, 2020, 2: 495-511
[13]	Ye J, Wang Y, Jin Z, et al. Dynamics of a predator-prey model with strong Allee effect and nonconstant mortality rate. Math Biosci Eng, 2022, 19(4): 3402-3426 doi: 10.3934/mbe.2022157 pmid: 35341257
[14]	李海侠. 一类食物链模型正解的稳定性和唯一性. 数学物理学报, 2017, 37A(6): 1094-1104
	Li H X. Stability and uniqueness of positive solutions for a food-chain model. Acta Math Sci, 2017, 37A(6): 1094-1104
[15]	Li H X, Li Y L, Yang W B. Existence and asymptotic behavior of positive solutions for a one-prey and two-competing-predators system with diffusion. Nonlinear Anal: RWA, 2016, 27: 261-282 doi: 10.1016/j.nonrwa.2015.07.010
[16]	Dancer E N. On the indices of fixed points of mappings in cones and applications. J Math Anal Appl, 1983, 91(1): 131-151 doi: 10.1016/0022-247X(83)90098-7
[17]	Jia Y, Wu J, Nie H. The coexistence states of a predator-prey model with nonmonotonic functional response and diffusion. Acta Appl Math, 2009, 108(2): 413-428 doi: 10.1007/s10440-008-9319-y
[18]	Crandall M G, Rabinowitz P H. Bifurcation from simple eigenvalues. J Funct Anal, 1971, 8(2): 321-340 doi: 10.1016/0022-1236(71)90015-2
[19]	Wu J H. Global bifurcation of coexistence state for a competition model in the chemostat. Nonlinear Anal, 2000, 39(7): 817-835 doi: 10.1016/S0362-546X(98)00250-8
[20]	Rabinowitz P H. Some global results for nonlinear eigenvalue problems. J Funct Anal, 1971, 7(3): 487-513 doi: 10.1016/0022-1236(71)90030-9
[21]	Cano-Casanova S. Existence and structure of the set of positive solutions of a general class of sublinear elliptic non-classical mixed boundary value problems. Nonlinear Anal: TMA, 2002, 49(3): 361-430 doi: 10.1016/S0362-546X(01)00116-X
[22]	Pao C V. Quasisolutions and global attractor of reaction-diffusion systems. Nonlinear Anal: TMA, 1996, 26(12): 1889-1903 doi: 10.1016/0362-546X(95)00058-4

Dynamics Analysis of a Diffusive Predator-Prey Model with Beddington-DeAngelis Function Response and Harvesting

RichHTML

PDF (PC)

Abstract

Cite this article

share this article

Figures/Tables 5

References 22

Related Articles 15

Metrics

Comments

Recommended 10

[1]	Xu Fei, Zhang Yong. Uniqueness and Asymptotic Stability of Time-Periodic Solutions for the Fractional Burgers Equation [J]. Acta mathematica scientia,Series A, 2023, 43(6): 1710-1722.
[2]	Ma Yani, Yuan Hailong. Bifurcation Analysis of a Class of Gierer-Meinhardt Activation Inhibition Model with Time Delay [J]. Acta mathematica scientia,Series A, 2023, 43(6): 1774-1788.
[3]	Pang Yuting, Zhao Dongxia. The PDP Feedback Control and Exponential Stabilization of a Star-Shaped Open Channels Network System [J]. Acta mathematica scientia,Series A, 2023, 43(6): 1803-1813.
[4]	Li Xiaodong, Gao Hongliang, Xu Jing. Exact Multiplicity of Positive Solutions for a Semipositone Mean Curvature Problem with Concave Nonlinearity [J]. Acta mathematica scientia,Series A, 2023, 43(5): 1341-1349.
[5]	Pang Yuting,Zhao Dongxia,Zhao Xin,Gao Caixia. The PDP Boundary Control for a Class of 2$\times$2 Hyperbolic Partial Differential System [J]. Acta mathematica scientia,Series A, 2023, 43(5): 1471-1482.
[6]	Liao Yuankang. Nonlinear Stability of Viscous Shock Waves for One-dimensional Isentropic Compressible Navier-Stokes Equations with Density-Dependent Viscosity [J]. Acta mathematica scientia,Series A, 2023, 43(4): 1149-1169.
[7]	He Xuyang,Mao Mingzhi,Zhang Tengfei. Existence and Stability of a Class of Impulsive Neutral Stochastic Functional Differential Equations with Poisson Jump [J]. Acta mathematica scientia,Series A, 2023, 43(4): 1221-1243.
[8]	Li Jize,Qiu Jixiu,Zhou Yonghui. Anticipative Nonlinear Filtering Equations Affected by Observation Noises and Stability of Linear Filtering [J]. Acta mathematica scientia,Series A, 2023, 43(4): 1244-1254.
[9]	Zhang Haiqun. Bounded Rationality and Stability of Weakly Efficient Nash Equilibria for a Class of Population Games [J]. Acta mathematica scientia,Series A, 2023, 43(4): 1311-1320.
[10]	Li Xiaoli,Chen Xiaoli. Stability and Exponential Decay of the 3D Boussinesq Equations with Partial Dissipation [J]. Acta mathematica scientia,Series A, 2023, 43(3): 754-770.
[11]	Wu Wenjun,Yang Guanghui,Fang Caiya,Yang Hui. Generic Stability of Cooperative Equilibria for Leader-Follower Population Games [J]. Acta mathematica scientia,Series A, 2023, 43(3): 921-929.
[12]	Fu Qinhong, Xiong Lianglin, Zhang Haiyang, Qin Ya, Quan Shenai. Sliding Mode Control for Time-Varying Delay Systems with Semi-Markov Jump [J]. Acta mathematica scientia,Series A, 2023, 43(2): 549-562.
[13]	Liu Lili, Wang Honggang, Li Yazhi. A Generalized HBV Diffusive Model with DNA-Containing Capsids and Cell-Cell Infection [J]. Acta mathematica scientia,Series A, 2023, 43(2): 604-624.
[14]	Song Huijuan, Huang Qian, Wang Zejia. Asymptotic Analysis of a Tumor Model with Angiogenesis and a Periodic Supply of External Nutrients [J]. Acta mathematica scientia,Series A, 2023, 43(1): 261-273.
[15]	Bo Li,Ziwei Liang. Stability of Stage-Structured Predator-Prey Models with Beddington-DeAngelis Functional Response [J]. Acta mathematica scientia,Series A, 2022, 42(6): 1826-1835.