Acta mathematica scientia,Series A ›› 2023, Vol. 43 ›› Issue (6): 1914-1928.
Previous Articles Next Articles
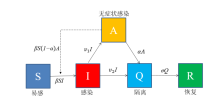
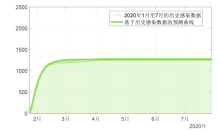
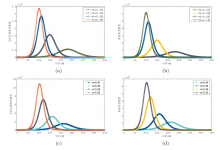
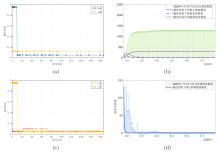
Dynamic Analysis and Optimal Control of an SIAQR Transmission Model with Asymptomatic Infection and Isolation
Zhong Yi1( ),Wang Yi1,*(
),Wang Yi1,*( ),Jiang Tianhe2
),Jiang Tianhe2
- 1School of Mathematics and Physics, China University of Geosciences Wuhan, Wuhan 430074
2School of Mathematics and Physics, Guangxi University for Nationalities, Nanning 530006
-
Received:2022-07-03Revised:2023-08-16Online:2023-12-26Published:2023-11-16 -
Supported by:National Natural Science Foundation of China(12171443);National Natural Science Foundation of China(11801532);Fundamental Research Funds for the Central Universities, China University of Geosciences (Wuhan)(CUGQT2023001)
CLC Number:
- O175
Cite this article
Zhong Yi, Wang Yi, Jiang Tianhe. Dynamic Analysis and Optimal Control of an SIAQR Transmission Model with Asymptomatic Infection and Isolation[J].Acta mathematica scientia,Series A, 2023, 43(6): 1914-1928.
share this article
| [1] | 跟踪严重急性呼吸综合症冠状病毒 2 变异株. https://www.who.int/zh/activities/tracking-SARS-CoV-2-variants [2022-4-14] |
| [2] | 2019 冠状病毒病 (COVID-19) 疫情. https://www.who.int/zh/emergencies/diseases/novel-coronavirus-2019 [2022-4-14] |
| [3] |
Wang X, Wu H, Tang S. Assessing age-specific vaccination strategies and post-vaccination reopening policies for COVID-19 control using SEIR modeling approach. Bulletin of Mathematical Biology, 2022, 84(10): 108
doi: 10.1007/s11538-022-01064-w pmid: 36029391 |
| [4] |
Tang B, Wang X, Li Q, et al. Estimation of the transmission risk of the 2019-nCoV and its implication for public health interventions. Journal of Clinical Medicine, 2020, 9(2): 462
doi: 10.3390/jcm9020462 |
| [5] |
Bushnaq S, Saeed T, Torres D F M, et al. Control of COVID-19 dynamics through a fractional-order model. Alexandria Engineering Journal, 2021, 60(4): 3587-3592
doi: 10.1016/j.aej.2021.02.022 |
| [6] |
Liu Z, Magal P, Seydi O, et al. Predicting the cumulative number of cases for the COVID-19 epidemic in China from early data. Mathematical Biosciences and Engineering, 2020, 17(4): 3040-3051
doi: 10.3934/mbe.2020172 pmid: 32987515 |
| [7] |
Liu Z, Magal P, Webb G. Predicting the number of reported and unreported cases for the COVID-19 epidemics in China, South Korea, Italy, France, Germany and United Kingdom. Journal of Theoretical Biology, 2021, 509: 110501
doi: 10.1016/j.jtbi.2020.110501 |
| [8] |
Lemos-Paiao A P, Silva C J, Torres D F M, et al. Optimal control of aquatic diseases: A case study of Yemen's cholera outbreak. Journal of Optimization Theory and Applications, 2020, 185(3): 1008-1030
doi: 10.1007/s10957-020-01668-z |
| [9] |
Lee W, Liu S, Tembine H, et al. Controlling propagation of epidemics via mean-field control. SIAM Journal on Applied Mathematics, 2021, 81(1): 190-207
doi: 10.1137/20M1342690 |
| [10] | Castilho C. Optimal control of an epidemic through educational campaigns. Electronic Journal of Differential Equations (EJDE)[electronic only], 2006, 2006: Paper No 125 |
| [11] | Anita S, Arnautu V, Capasso V, et al. An Introduction to Optimal Control Problems in Life Sciences and Economics: From Mathematical Models to Numerical Simulation with MATLAB. Basel: Birkhauser, 2011 |
| [12] | 黄森忠, 彭志行, 靳祯. 新型冠状病毒肺炎疫情控制策略研究:效率评估及建议. 中国科学: 数学, 2020, 50(6): 885-898 |
| Huang S Z, Peng Z X, Jin Z. Study on the control strategy of novel coronavirus pneumonia outbreak: Efficiency assessment and recommendations. Science China Mathematics, 2020, 50(6): 885-898 | |
| [13] | Martcheva M. An Introduction to Mathematical Epidemiology. New York: Springer, 2015 |
| [14] | Coppel W A. Stability and Asymptotic Behavior of Differential Equations. Boston: Heath, 1965 |
| [15] |
Van den Driessche P, Watmough J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Mathematical Biosciences, 2002, 180(1/2): 29-48
doi: 10.1016/S0025-5564(02)00108-6 |
| [16] |
Diekmann O, Heesterbeek J A P, Metz J A J. On the definition and the computation of the basic reproduction ratio R0 in models for infectious diseases in heterogeneous populations. Journal of Mathematical Biology, 1990, 28: 365-382
doi: 10.1007/BF00178324 pmid: 2117040 |
| [17] |
Wang Y, Wei Z, Cao J. Epidemic dynamics of influenza-like diseases spreading in complex networks. Nonlinear Dynamics, 2020, 101: 1801-1820
doi: 10.1007/s11071-020-05867-1 |
| [18] |
Bidari S, Chen X, Peters D, et al. Solvability of implicit final size equations for SIR epidemic models. Mathematical Biosciences, 2016, 282: 181-190
doi: 10.1016/j.mbs.2016.10.012 |
| [19] | Rodrigues H S F. Optimal Control and Numerical Optimization Applied to Epidemiological Models. Portugal: Universidade de Aveiro, 2012 |
| [20] |
Brandeau M L, Zaric G S, Richter A. Resource allocation for control of infectious diseases in multiple independent populations: Beyond cost-effectiveness analysis. Journal of Health Economics, 2003, 22(4): 575-598
pmid: 12842316 |
| [21] |
Kumar A, Srivastava P K, Takeuchi Y. Modeling the role of information and limited optimal treatment on disease prevalence. Journal of Theoretical Biology, 2017, 414: 103-119
doi: S0022-5193(16)30382-4 pmid: 27890574 |
| [22] | 浙江政务服务网疫情防控专区. https://www.zjzwfw.gov.cn/zjservice/yqfk/page.do [2022-4-14] |
| [23] |
Andrieu C, De Freitas N, Doucet A, et al. An introduction to MCMC for machine learning. Machine learning, 2003, 50: 5-43
doi: 10.1023/A:1020281327116 |
| [24] |
Tilahun G T, Alemneh H T. Mathematical modeling and optimal control analysis of COVID-19 in Ethiopia. Journal of Interdisciplinary Mathematics, 2021, 24(8): 2101-2120
doi: 10.1080/09720502.2021.1874086 |
| [25] |
Wei F, Xue R. Stability and extinction of SEIR epidemic models with generalized nonlinear incidence. Mathematics and Computers in Simulation, 2020, 170: 1-15
doi: 10.1016/j.matcom.2018.09.029 |
| [26] |
Li D, Wei F, Mao X. Stationary distribution and density function of a stochastic SVIR epidemic model. Journal of the Franklin Institute, 2022, 359(16): 9422-9449
doi: 10.1016/j.jfranklin.2022.09.026 |
| [27] |
Cadoni M. How to reduce epidemic peaks keeping under control the time-span of the epidemic. Chaos, Solitons and Fractals, 2020, 138: 109940
doi: 10.1016/j.chaos.2020.109940 |
| [1] |
Lu Weiping,Liu Hanbing.
Sampled-Data Time Optimal Control for Heat Equation with Potential in |
| [2] | Zeng Biao. Optimal Control for a Class of Nonlinear Evolutionary Equations with Weakly Continuous Operators [J]. Acta mathematica scientia,Series A, 2023, 43(2): 515-530. |
| [3] | Zhenxiang Hu,Linfei Nie. Analysis of a Reaction-Diffusion Epidemic Model with Horizontal Transmission and Environmental Transmission [J]. Acta mathematica scientia,Series A, 2022, 42(6): 1849-1860. |
| [4] | Xiaoyong Cui,Can Zhang. Turnpike Properties of a Class of Optimal Control Problems with Exponential Weights [J]. Acta mathematica scientia,Series A, 2022, 42(4): 1256-1264. |
| [5] | Kai Wang,Hongyong Zhao. Traveling Wave of a Reaction-Diffusion Dengue Epidemic Model with Time Delays [J]. Acta mathematica scientia,Series A, 2022, 42(4): 1209-1226. |
| [6] | Zerong He,Yimeng Dou,Mengjie Han. Optimal Boundary Control for a Hierarchical Size-Structured Population Model with Delay [J]. Acta mathematica scientia,Series A, 2022, 42(3): 867-880. |
| [7] | Tailei Zhang,Junli Liu,Mengjie Han. Dynamics of an Anthrax Epidemiological Model with Time Delay and Seasonality [J]. Acta mathematica scientia,Series A, 2022, 42(3): 851-866. |
| [8] | Zerong He,Nan Zhou. Optimal Harvesting in a Competing System of Hierarchical Age-Structured Populations [J]. Acta mathematica scientia,Series A, 2022, 42(1): 228-244. |
| [9] | Dandan Sun,Yingke Li,Zhidong Teng,Tailei Zhang. Analysis of the Stability for Measles Epidemic Model with Age-Structured [J]. Acta mathematica scientia,Series A, 2021, 41(6): 1950-1968. |
| [10] | Zerong He,Mengjie Han. Optimal Control of Initial Distributions in a Hierarchical Size-Structured Population System with Delay [J]. Acta mathematica scientia,Series A, 2021, 41(4): 1181-1191. |
| [11] | Lixiang Feng,Defen Wang. Global Stability of an Epidemic Model with Quarantine and Incomplete Treatment [J]. Acta mathematica scientia,Series A, 2021, 41(4): 1235-1248. |
| [12] |
Qionglin Liu,Yinghui Tang.
Analysis of |
| [13] | Le Luo,Yinghui Tang. System Capacity Optimization Design and Optimal Control Policy (N*, D*) for M/G/1 Queue with p-Entering Discipline and Min(N, D, V)-Policy [J]. Acta mathematica scientia,Series A, 2019, 39(5): 1228-1246. |
| [14] | Xiaojie Jing, Aimin Zhao, Guirong Liu. Global Stability of a Measles Epidemic Model with Partial Immunity and Environmental Transmission [J]. Acta mathematica scientia,Series A, 2019, 39(4): 909-917. |
| [15] | Maoning Tang,Qingxin Meng. Linear-Quadratic Optimal Control Problems for Mean-Field Backward Stochastic Differential Equations with Jumps [J]. Acta mathematica scientia,Series A, 2019, 39(3): 620-637. |
| Viewed | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
Full text 332
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Abstract 117
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
Cited |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
| Shared | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Discussed | ||||||||||||||||||||||||||||||||||||||||||||||||||
|