Acta mathematica scientia,Series A ›› 2022, Vol. 42 ›› Issue (6): 1898-1921.
A Hybrid Algorithm for Solving Truncated Complex Singular Value Decomposition
Yuxin Zhang1,Wenting Hou1,Xuelin Zhou2,1,*( ),Jiaofen Li1
),Jiaofen Li1
- 1 School of Mathematics and Computational Science, Center for Applied Mathematics of Guangxi(GUET), Guangxi Colleges and Universities Key Laboratory of Data Analysis and Computation, Guilin University of Electronic Technology, Guangxi Guilin 541004
2 School of Mathematics and Statistics, Yunan University, Yunan Kunming 650000
-
Received:2021-06-19Online:2022-12-26Published:2022-12-16 -
Contact:Xuelin Zhou E-mail:zhouxuelin0309@163.com -
Supported by:the National Natural Science Foundation(12261026);the National Natural Science Foundation(11961012);the National Natural Science Foundation(12201149);the Special Fund for Science and Technological Bases and Talents of Guangxi(2021AC06001);the Guangxi College Student Innovation and Entrepreneurship Training Program(201810595215);the GUET Graduate Innovation Project(2022YCXS142);the Guangxi Key Laboratory of Automatic Detecting Technology and Instruments(YQ21103);the Guangxi Key Laboratory of Automatic Detecting Technology and Instruments(YQ22106)
CLC Number:
- O151.1
Cite this article
Yuxin Zhang,Wenting Hou,Xuelin Zhou,Jiaofen Li. A Hybrid Algorithm for Solving Truncated Complex Singular Value Decomposition[J].Acta mathematica scientia,Series A, 2022, 42(6): 1898-1921.
share this article
"
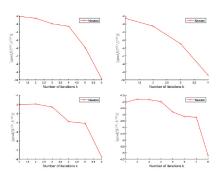
| L | CT.(s) | IT. | L | CT.(s) | IT. | |||
| 1 | 0.75 | 130 | 1.78 | 1 | 0.49 | 123 | 2.45 | |
| 2 | 0.60 | 161 | 5.78 | 2 | 0.39 | 95 | 1.27 | |
| 3 | 0.53 | 140 | 3.82 | 3 | 0.29 | 72 | 5.67 | |
| 4 | 0.30 | 71 | 9.47 | |||||
| 5 | 0.33 | 86 | 3.49 | |||||
| 1 | 0.84 | 148 | 7.49 | 1 | 0.26 | 69 | 2.77 | |
| 2 | 0.75 | 142 | 5.82 | 2 | 0.50 | 129 | 5.91 | |
| 3 | 0.44 | 113 | 8.08 | 3 | 0.47 | 118 | 3.28 | |
| 4 | 0.49 | 132 | 4.50 | 4 | 0.63 | 147 | 9.80 | |
| 5 | 0.23 | 59 | 6.50 | 5 | 0.43 | 112 | 2.45 | |
| 6 | 0.59 | 149 | 1.24 | |||||
| 7 | 0.29 | 77 | 4.70 | |||||
"
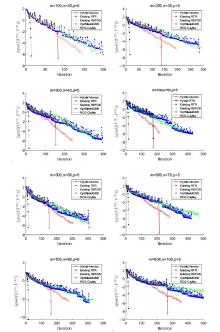
| CT.(s) | IT. | Grad. | Obj. | CT.(s) | IT. | Grad. | Obj. | ||
| Hybrid-Newton | 0.32 | 80/3 | 1.92 | -116.67 | 1.21 | 134/3 | 1.29 | -156.31 | |
| Existing-RTR | 0.38 | 13 | 5.38 | -116.67 | 0.83 | 14 | 5.35 | -156.31 | |
| Existing-RBFGS | 3.93 | 145 | 9.87 | -116.67 | 5.14 | 194 | 8.56 | -156.31 | |
| OptStifelGBB | 0.06 | 199 | 8.87 | -116.67 | 0.16 | 284 | 2.14 | -156.31 | |
| RCG-Cayley | 0.10 | 182 | 8.63 | -116.67 | 0.28 | 293 | 9.15 | -156.31 | |
| Hybrid-Newton | 2.64 | 149/5 | 1.33 | -189.95 | 4.80 | 173/3 | 4.90 | -223.22 | |
| Existing-RTR | 0.99 | 15 | 2.62 | -189.95 | 1.37 | 15 | 5.17 | -223.22 | |
| Existing-RBFGS | 6.70 | 239 | 9.54 | -189.95 | 6.51 | 216 | 9.83 | -223.22 | |
| OptStifelGBB | 0.37 | 396 | 4.04 | -189.95 | 0.47 | 430 | 9.49 | -223.22 | |
| RCG-Cayley | 0.50 | 362 | 9.08 | -189.95 | 0.64 | 363 | 9.98 | -223.22 | |
| Hybrid-Newton | 5.26 | 148/2 | 2.80 | -245.29 | 10.95 | 210/ 4 | 2.46 | -272.71 | |
| Existing-RTR | 1.45 | 14 | 3.48 | -245.29 | 1.51 | 15 | 3.14 | -272.71 | |
| Existing-RBFGS | 9.60 | 304 | 2.45 | -245.29 | 9.49 | 285 | 1.30 | -272.71 | |
| OptStifelGBB | 0.61 | 408 | 3.60 | -245.29 | 0.75 | 423 | 8.00 | -272.71 | |
| RCG-Cayley | 0.84 | 406 | 7.70 | -245.29 | 1.15 | 471 | 8.49 | -272.71 | |
| Hybrid-Newton | 16.85 | 159/4 | 6.93 | -293.84 | 21.11 | 265/3 | 2.21 | -316.66 | |
| Existing-RTR | 2.26 | 15 | 2.24 | -293.84 | 3.11 | 15 | 4.91 | -316.66 | |
| Existing-RBFGS | 11.99 | 275 | 2.59 | -293.84 | 18.02 | 355 | 7.76 | -316.66 | |
| OptStifelGBB | 0.89 | 408 | 8.12 | -293.84 | 2.62 | 587 | 9.07 | -316.66 | |
| RCG-Cayley | 1.32 | 438 | 8.16 | -293.84 | 5.44 | 835 | 8.26 | -316.66 | |
| 1 |
Hansen P C . Truncated singular value decomposition solutions to discrete ill-posed problems with ill-determined numerical rank. SIAM Journal on Scientific and Statistical Computing, 1990, 11 (3): 503- 518
doi: 10.1137/0911028 |
| 2 |
Noschese S , Reichel L . A modified truncated singular value decomposition method for discrete ill-posed problems. Numerical Linear Algebra with Applications, 2014, 21 (6): 813- 822
doi: 10.1002/nla.1938 |
| 3 | 余景景, 刘芳, 焦李成等. 截断奇异值分解的生物发光断层成像重建问题. 西北大学学报(自然科学版), 2009, 39(5): 755-760 |
| Yu J, Liu F, Jiao L, He X. Research on the reconstruction for bioluminescence tomography using truncated singular value decomposition method. Journal of Northwest University (Natural Science Edition), 2009, 39(5): 755-760 | |
| 4 | Doğu S , Akıncı M N , Çayören M , Akduman İ . Truncated singular value decomposition for through-the-wall microwave imaging application. IET Microwaves, Antennas & Propagation, 2019, 14 (4): 260- 267 |
| 5 | Francischello R , Geppi M , Flori A , et al. Application of low-rank approximation using truncated singular value decomposition for noise reduction in hyperpolarized 13C NMR spectroscopy. NMR in Biomedicine, 2021, 34 (5): e4285 |
| 6 | Sato H . Riemannian Optimization and Its Applications. Switzerland: Springer Nature, 2021 |
| 7 |
Sato H , Iwai T . A Riemannian optimization approach to the matrix singular value decomposition. SIAM Journal on Optimization, 2013, 23 (1): 188- 212
doi: 10.1137/120872887 |
| 8 | Sato H. Riemannian conjugate gradient method for complex singular value decomposition problem. 53rd IEEE Conference on Decision and Control, 2015, pages 5849-5854 |
| 9 | Sato H, Iwai T. A complex singular value decomposition algorithm based on the Riemannian Newton method[C]//52nd IEEE Conference on Decision and Control. Firenze: IEEE, 2013: 2972-2978 |
| 10 |
Aihara K , Sato H . A matrix-free implementation of Riemannian Newton's method on the Stiefel manifold. Optimization Letters, 2017, 11, 1729- 1741
doi: 10.1007/s11590-016-1090-9 |
| 11 |
Xu W W , Li W , Zhu L , Huang X P . The analytic solutions of a class of constrained matrix minimization and maximization problems with applications. SIAM Journal on Optimization, 2019, 29 (2): 1657- 1686
doi: 10.1137/17M1140777 |
| 12 | Wen Z , Yin W . A feasible method for optimization with orthogonality constraints. Mathematical Programming, 2013, 142 (1/2): 397- 434 |
| 13 | Absil P A , Mahony R , Sepulchre R . Optimization Algorithms on Matrix Manifolds. Princeton: Princeton University Press, 2008, |
| 14 |
Hu J , Liu X , Wen Z W , Yuan Y X . A brief introduction to manifold optimization. Journal of the Operations Research Society of China, 2020, 8 (2): 199- 248
doi: 10.1007/s40305-020-00295-9 |
| 15 | Absil P A, Mahony R, Trumpf J. An extrinsic look at the Riemannian Hessian[C]//International Conference on Geometric Science of Information. Berlin: Springer, 2013: 361-368 |
| 16 |
Henderson H V , Searle S R . The vec-permutation matrix, the vec operator and Kronecker products: A review. Linear and Multilinear Algebra, 1981, 9 (4): 271- 288
doi: 10.1080/03081088108817379 |
| 17 | Yuan S , Liao A , Lei Y . Least squares Hermitian solution of the matrix equation (AXB, CXD)=(E, F) with the least norm over the skew field of quaternions. Mathematical and Computer Modelling, 2008, 48 (1/2): 91- 100 |
| 18 | Saad Y . Iterative Methods for Sparse Linear Systems. Philadelphia: SIAM, 2003 |
| 19 | Boumal N , Mishra B , Absil P A , Sepulchre R . Manopt, a Matlab toolbox for optimization on manifolds. Journal of Machine Learning Research, 2014, 15 (1): 1455- 1459 |
| 20 |
Zhu X . A Riemannian conjugate gradient method for optimization on the Stiefel manifold. Computational Optimization and Applications, 2017, 67 (1): 73- 110
doi: 10.1007/s10589-016-9883-4 |
| 21 | Dai Y . A nonmonotone conjugate gradient algorithm for unconstrained optimization. Journal of System Science and Complexity, 2002, 15, 139- 145 |
| 22 | Li J F , Li W , Vong S W , et al. A Riemannian optimization approach for solving the generalized eigenvalue problem for nonsquare matrix pencils. Journal of Scientific Computing, 2020, 82 (3): 1- 43 |
| [1] | GAO Xing-Hui, ZHOU Hai-Yun, GAO Gai-Liang. Hybrid Algorithms of Common Elements for Equilibrium Problems and Fixed Point Problems [J]. Acta mathematica scientia,Series A, 2011, 31(3): 720-728. |
|