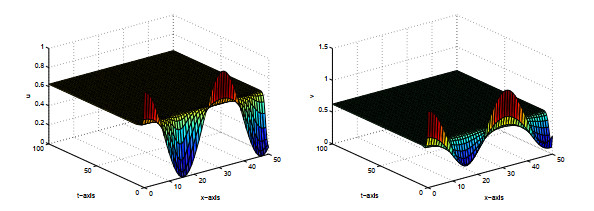
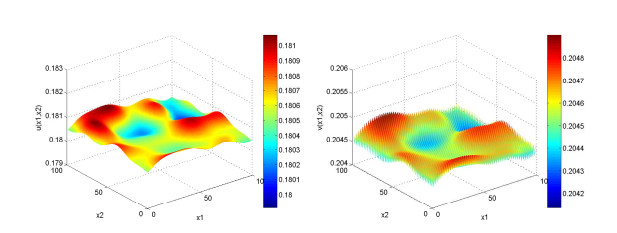
Acta mathematica scientia,Series A ›› 2022, Vol. 42 ›› Issue (5): 1575-1591.
Previous Articles Next Articles
Dynamics and Patterns for a Diffusive Leslie-Gower Predator-Prey Model with Michaelis-Menten Type Harvesting in Prey
Zhanping Ma1,Haifeng Huo2,*( ),Hong Xiang2
),Hong Xiang2
- 1 School of Mathematics and Information Science, Henan Polytechnic University, Jiaozuo, Henan 454003
2 Department of Applied Mathematics, Lanzhou University of Technology, Lanzhou 730050
-
Received:2021-07-23Online:2022-10-26Published:2022-09-30 -
Contact:Haifeng Huo E-mail:hfhuo@lut.edu.cn -
Supported by:the NSFC(11861044);the NSFC(11661050);the NSF of Gansu of China(21JR7RA212);the NSF of Gansu of China(21JR7RA535)
CLC Number:
- O175
Cite this article
Zhanping Ma,Haifeng Huo,Hong Xiang. Dynamics and Patterns for a Diffusive Leslie-Gower Predator-Prey Model with Michaelis-Menten Type Harvesting in Prey[J].Acta mathematica scientia,Series A, 2022, 42(5): 1575-1591.
share this article
| 1 |
Berryman A A . The orgins and evolution of predator-prey theory. Ecology, 1992, 73, 1530- 1535
doi: 10.2307/1940005 |
| 2 |
May R M . Limit cycles in predator-prey communities. Science, 1972, 177, 900- 902
doi: 10.1126/science.177.4052.900 |
| 3 | Bacaër N . A Short History of Mathematical Population Dynamics. New York: Springer Verlag, 2011 |
| 4 |
Braza P A . The bifurcation structure of the Holling-Tanner model for predator-prey interactions using two-timing. SIAM J Appl Math, 2003, 63, 889- 904
doi: 10.1137/S0036139901393494 |
| 5 |
吴鑫, 袁荣, 马兆海. 非局部扩散Holling-Tanner捕食者-食饵系统的临界与非临界行波解分析. 数学物理学报, 2021, 41A (6): 1705- 1717
doi: 10.3969/j.issn.1003-3998.2021.06.011 |
|
Wu X , Yuan R , Ma Z H . Analysis on critical waves and non-critical waves for Holling-Tanner predator-prey system with nonlocal diffusion. Acta Math Sci, 2021, 41A (6): 1705- 1717
doi: 10.3969/j.issn.1003-3998.2021.06.011 |
|
| 6 |
Guo S . Bifurcation and spatio-temporal patterns in a diffusive predator-prey system. Nonlinear Anal Real World Appl, 2018, 42, 448- 477
doi: 10.1016/j.nonrwa.2018.01.011 |
| 7 |
Huang J , Liu S , Ruan S , Xiao D . Bifurcations in a discrete predator-prey model with nonmonotonic functional response. J Math Anal Appl, 2018, 464, 201- 230
doi: 10.1016/j.jmaa.2018.03.074 |
| 8 |
Wang J , Wei J , Shi J . Global bifurcation analysis and pattern formation in homogeneous diffusive predator-prey systems. J Differential Equations, 2016, 260, 3495- 3523
doi: 10.1016/j.jde.2015.10.036 |
| 9 | 王雪臣, 魏俊杰. 时滞在具有Ivlev型功能反应函数的捕食者-食饵扩散系统中的作用. 数学物理学报, 2014, 34A (2): 234- 250 |
| Wang X C , Wei J J . The effect of delay on a diffusive predator-prey system with Ivlev-type functional response. Acta Math Sci, 2014, 34A (2): 234- 250 | |
| 10 |
Du Y , Hsu S B . A diffusive predator-prey model in heterogeneous environment. J Differential Equations, 2004, 203, 331- 364
doi: 10.1016/j.jde.2004.05.010 |
| 11 |
Leslie P H , Gower J C . The properties of a stochastic model for the predator-prey type of interaction between two species. Biometrica, 1960, 47, 219- 234
doi: 10.1093/biomet/47.3-4.219 |
| 12 |
Hsu S B , Hwang T W . Global stability for a class of predator-prey systems. SIAM J Appl Math, 1995, 55, 763- 783
doi: 10.1137/S0036139993253201 |
| 13 |
Xiao D , Jennings L S . Bifurcations of a ratio-dependent predator-prey system with constant rate harvesting. SIAM J Appl Math, 2005, 65, 737- 753
doi: 10.1137/S0036139903428719 |
| 14 |
Chen J , Huang J , Ruan S , Wang J . Bifurcations of invariant tori in predator-prey models with seasonal prey harvesting. SIAM J Appl Math, 2013, 73, 1876- 1905
doi: 10.1137/120895858 |
| 15 |
May R M , Beddington J R , Clark C W , Holt S J , Laws R M . Management of multispecies fisheries. Science, 1979, 205, 267- 277
doi: 10.1126/science.205.4403.267 |
| 16 | Huang J , Gong Y , Ruan S . Bifurcation analysis in a predator-prey model with constant-yield predator harvesting. Discrete Contin Dynam Syst Ser B, 2013, 18, 2101- 2121 |
| 17 |
Beddington J R , May R M . Maximum sustainable yields in systems subject to harvesting at more than one trophic level. Math Biosci, 1980, 51, 261- 281
doi: 10.1016/0025-5564(80)90103-0 |
| 18 |
Beddington J R , Cooke J G . Harvesting from a prey-predator complex. Ecol Model, 1982, 14, 155- 177
doi: 10.1016/0304-3800(82)90016-3 |
| 19 |
Gong Y , Huang J . Bogdanov-Takens bifurcation in a Leslie-Gower predator-prey model with prey harvesting. Acta Math Appl Sinica Eng Ser, 2014, 30, 239- 244
doi: 10.1007/s10255-014-0279-x |
| 20 | Zhu C R , Lan K Q . Phase portraits, Hopf-bifurcations and limit cycles of Leslie-Gower predator-prey systems with harvesting rates. Discrete Contin Dyn Syst Ser B, 2010, 14, 289- 306 |
| 21 |
Gupta R P , Banerjee M , Chandra P . Bifurcation analysis and control of Leslie-Gower predator-prey model with Michaelis-Menten type prey-harvesting. Differ Equ Dyn Syst, 2012, 20, 339- 366
doi: 10.1007/s12591-012-0142-6 |
| 22 |
Kar T K , Chaudhuri K S . Regulation of a prey-predator fishery by taxation: a dynamic reaction model. J Biol Syst, 2003, 11, 173- 187
doi: 10.1142/S0218339003000828 |
| 23 | Clark C W . Aggregation and fishery dynamics: a theoretical study of schooling and the purse seine tuna fisheries. Fish Bull, 1979, 77, 317- 337 |
| 24 | Wu J . Theory and Applications of Partial Functional Differential Equations. New York: Springer-Verlag, 1996 |
| 25 | Turing A . The chemical basis of morphogenesis. Philos Trans R Soc Ser B, 1952, 237, 37- 72 |
| 26 | Pao C V . Nonlinear Parabolic and Elliptic Equations. New York: Plenum Publishing Corporation, 1992, |
| 27 |
Lou Y , Ni W M . Diffusion, self-diffusion and cross-diffusion. J Differential Equations, 1996, 131, 79- 131
doi: 10.1006/jdeq.1996.0157 |
| 28 |
Lin C S , Ni W M , Takagi I . Large amplitude stationary solutions to a chemotais systems. J Differential Equations, 1988, 72, 1- 27
doi: 10.1016/0022-0396(88)90147-7 |
| 29 | Nirenberg L . Topics in Nonlinear Functional Analysis. Providence: American Mathematical Society, 2001, |
| 30 | 张晓. Matlab微分方程高效解法: 谱方法原理与实现. 北京: 机械工业出版社, 2015 |
| Zhang X . Matlab Efficient Method of Differential Equation: Principle and Implementation of Spectral Method. Beijing: China Machine Press, 2015 |
| [1] | Zhenxiang Hu,Linfei Nie. Analysis of a Reaction-Diffusion Epidemic Model with Horizontal Transmission and Environmental Transmission [J]. Acta mathematica scientia,Series A, 2022, 42(6): 1849-1860. |
| [2] | Dandan Sun,Yingke Li,Zhidong Teng,Tailei Zhang. Analysis of the Stability for Measles Epidemic Model with Age-Structured [J]. Acta mathematica scientia,Series A, 2021, 41(6): 1950-1968. |
| [3] | Gui Zhanji; Jia Jing; Ge Weigao. Global Stability of Single-species Diffusion Models with Time Delay [J]. Acta mathematica scientia,Series A, 2007, 27(3): 496-505. |
| [4] |
WEN Xian-Zhang.
The Uniform Persistence of PredatorPrey Systems with Delays [J]. Acta mathematica scientia,Series A, 2003, 23(1): 96-105. |
| Viewed | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
Full text 168
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Abstract 157
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
Cited |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
| Shared | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Discussed | ||||||||||||||||||||||||||||||||||||||||||||||||||
|