Acta mathematica scientia,Series A ›› 2022, Vol. 42 ›› Issue (3): 775-783.
Previous Articles Next Articles
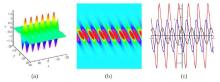
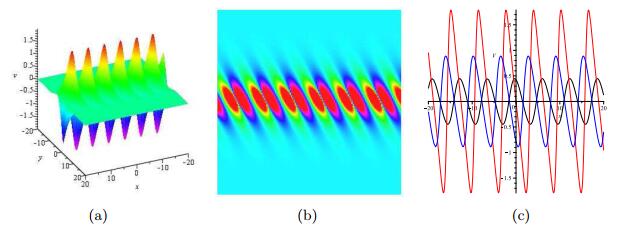
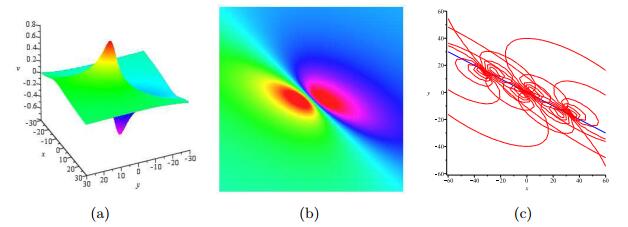
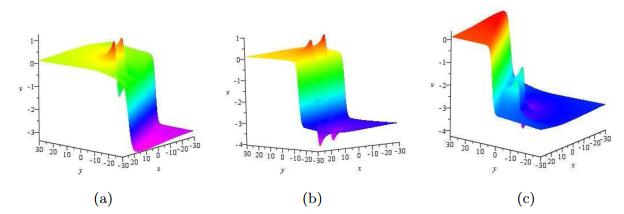
Breather Wave Solutions, Lump Solutions and Semi-Rational Solutions of a Reduced (3+1)Dimensional Hirota Equation
Chunmei Fang1,*( ),Shoufu Tian2(
),Shoufu Tian2( )
)
- 1 Department of Mathematics and Statistics, Jining Normal University, Inner Mongolia Ulanqab 012000
2 Department of Mathematics, China University of Mining and Technology, Jiangsu Xuzhou 221116
-
Received:2021-07-22Online:2022-06-26Published:2022-05-09 -
Contact:Chunmei Fang E-mail:dllgfcmmxl@163.com;shoufu2006@126.com -
Supported by:the NSFC(11975306);the Higher Educational Scientific Research Projects of Inner Mongolia Autonomous Region(NJZY20248);the Higher Educational Scientific Research Projects of Inner Mongolia Autonomous Region(NJZY22307)
CLC Number:
- O175.24
Cite this article
Chunmei Fang,Shoufu Tian. Breather Wave Solutions, Lump Solutions and Semi-Rational Solutions of a Reduced (3+1)Dimensional Hirota Equation[J].Acta mathematica scientia,Series A, 2022, 42(3): 775-783.
share this article
| 1 | Hirota R . The Direct Method in Soliton Theory. Cambridge: Cambridge University Press, 2004 |
| 2 | 楼森岳, 唐晓艳. 非线性数学物理方法. 北京: 科学出版社, 2006 |
| Lou S Y , Tang X Y . Nonlinear Mathematical Physics Methods. Beijing: Science Press, 2006 | |
| 3 |
郝晓红, 程智龙. 一类广义浅水波KdV方程的可积性研究. 数学物理学报, 2019, 39A (3): 451- 460
doi: 10.3969/j.issn.1003-3998.2019.03.005 |
|
Hao X H , Cheng Z L . The integrability of the KdV-shallow water wave equation. Acta Math Sci, 2019, 39A (3): 451- 460
doi: 10.3969/j.issn.1003-3998.2019.03.005 |
|
| 4 |
Wazwaz A M . Gaussian solitary wave solutions for nonlinear evolution equations with logarithmic nonlinearities. Nonlinear Dyn, 2016, 83, 591- 596
doi: 10.1007/s11071-015-2349-x |
| 5 |
Ginzburg N S , Rozental R M , Sergeev A S , et al. Generation of rogue waves in gyrotrons operating in the regime of developed turbulence. Phys Rev Lett, 2017, 119 (3): 034801
doi: 10.1103/PhysRevLett.119.034801 |
| 6 |
Onorato M , Residori S , Bortolozzo U , et al. Rogue waves and their generating mechanisms in different physical contexts. Phys Rep, 2013, 528 (2): 47- 89
doi: 10.1016/j.physrep.2013.03.001 |
| 7 |
Rao J G , Zhang Y S , Athanassios S F , He J S . Rogue waves of the nonlocal Davey-Stewartson I equation. Nonlinearity, 2018, 31, 4090- 4107
doi: 10.1088/1361-6544/aac761 |
| 8 |
Ma W X , Yong X L , Lü X . Soliton solutions to the B-type Kadomtsev-Petviashvili equation under general dispersion relations. Wave Motion, 2021, 103, 102719
doi: 10.1016/j.wavemoti.2021.102719 |
| 9 |
Ma W X . N-soliton solution of a combined pKP-BKP equation. J Geom Phys, 2021, 165, 104191
doi: 10.1016/j.geomphys.2021.104191 |
| 10 | Ma W X . N-soliton solutions and the Hirota conditionsin (1+1)-dimensions. Int J Nonlinear Sci Numer Simul, 2021, |
| 11 |
Ma W X . N-soliton solutions and the Hirota conditions in (2+1)-dimensions. Opt Quantum Electron, 2020, 52, 511
doi: 10.1007/s11082-020-02628-7 |
| 12 | Ma W X . N-soliton solution and the Hirota condition of a (2+1)-dimensional combined equation. Math Comput Simulat, 2021, 190 (C): 270- 279 |
| 13 |
Ma W X . Lump solutions to the Kadomtsev-Petviashvili equation. Phys Lett A, 2015, 379 (36): 1975- 1978
doi: 10.1016/j.physleta.2015.06.061 |
| 14 |
Ma W X , Qin Z Y , Lü X . Lump solutions to dimensionally reduced p-gKP and p-gBKP equations. Nonlinear Dyn, 2016, 84, 923- 931
doi: 10.1007/s11071-015-2539-6 |
| 15 |
Tian S F . Asymptotic behavior of a weakly dissipative modified two-component Dullin-Gottwald-Holm system. Appl Math Lett, 2018, 83, 65- 72
doi: 10.1016/j.aml.2018.03.019 |
| 16 | Ablowitz M J , Satsuma J . Solitons and rational solutions of nonlinear evolution equations. J Math Phys, 1978, 19 (10): 2180- 2186 |
| 17 |
Satsuma J , Ablowitz M J . Two-dimensional lumps in nonlinear dispersive systems. J Math Phys, 1979, 20, 1496- 1503
doi: 10.1063/1.524208 |
| 18 |
Huang L L , Chen Y . Lump solutions and interaction phenomenon for (2+1)-dimensional Sawada-Kotera equation. Commun Theor Phys, 2017, 67, 473- 478
doi: 10.1088/0253-6102/67/5/473 |
| 19 | Tian S F , Zhang T T . Long-time asymptotic behavior for the Gerdjikov-Ivanov type of derivative nonlinear Schrodinger equation with time-periodic boundary condition. Proc Am Math Soc, 2018, 146 (4): 1713- 1729 |
| 20 |
Qian C , Rao J G , Liu Y B , He J S . Rogue waves in the three-dimensional Kadomtsev-Petviashvili equation. Chin Phys Lett, 2016, 33 (11): 110201
doi: 10.1088/0256-307X/33/11/110201 |
| 21 |
Peng W Q , Tian S F , Zhang T T . Analysis on lump, lumpoff and rogue waves with predictability to the (2+1)-dimensional B-type Kadomtsev-Petviashvili equation. Phys Lett A, 2018, 382, 2701- 2708
doi: 10.1016/j.physleta.2018.08.002 |
| 22 |
Liu Y K , Li B . Dynamics of rogue waves on multi-soliton background in the Benjamin Ono equation. Pramana, 2017, 88 (4): 57
doi: 10.1007/s12043-016-1361-0 |
| 23 |
Rao J G , Fokas A S , He J S . Doubly localized two-dimensional rogue waves in the Davey-Stewartson I equation. J Nonlinear Sci, 2021, 31, 67
doi: 10.1007/s00332-021-09720-6 |
| 24 |
Rao J G , Chow K W , Mihalache D , He J S . Completely resonant collision of lumps and line solitons in the Kadomtsev-Petviashvili I equation. Stud Appl Math, 2021, 147 (3): 1007- 1035
doi: 10.1111/sapm.12417 |
| 25 |
Rao J G , He J S , Mihalache D . Doubly localized rogue waves on a background of dark solitons for the Fokas system. Appl Math Lett, 2021, 121, 107435
doi: 10.1016/j.aml.2021.107435 |
| 26 |
Rao J G , Cheng Y , He J S . Rational and semi-rational solutions of the nonlocal Davey-Stewartson equations. Stud Appl Math, 2017, 139 (4): 568- 598
doi: 10.1111/sapm.12178 |
| 27 |
Gao L N , Zhao X Y , Zi Y Y . Resonant behavior of multiple wave solutions to a Hirota bilinear equation. Comput Math Appl, 2016, 72 (5): 1225- 1229
doi: 10.1016/j.camwa.2016.06.008 |
| 28 |
Dong M J , Tian S F , Yan X W , Zou L . Solitary waves, homoclinic breather waves and rogue waves of the (3+1)-dimensional Hirota bilinear equation. Comput Math Appl, 2018, 75 (3): 957- 964
doi: 10.1016/j.camwa.2017.10.037 |
| 29 |
Lü X , Ma W X . Study of lump dynamics based on a dimensionally reduced Hirota bilinear equation. Nonlinear Dyn, 2016, 85 (2): 1217- 1222
doi: 10.1007/s11071-016-2755-8 |
| 30 |
Wang C . Lump solution and integrability for the associated Hirota bilinear equation. Nonlinear Dyn, 2017, 87 (4): 2635- 2642
doi: 10.1007/s11071-016-3216-0 |
| [1] | Jiayu Liu,Hanyu Wei,Yan Zhang,Tiecheng Xia,Hui Wang. Soliton Solutions and Its Nonlinear Dynamics Behavior Research of the Three-Component Four-Order Nonlinear Schrödinger System in Alpha Helical Protein [J]. Acta mathematica scientia,Series A, 2022, 42(6): 1873-1885. |
| [2] | Qinghua Zhang,Yueping Zhu. Weighted Temporal-Spatial Estimates of the Stokes Semigroup with Applications to the Non-Stationary Navier-Stokes Equation in Half-Space [J]. Acta mathematica scientia,Series A, 2021, 41(6): 1657-1670. |
| [3] | Xiaohong Hao,Zhilong Cheng. The Integrability of the KdV-Shallow Water Waves Equation [J]. Acta mathematica scientia,Series A, 2019, 39(3): 451-460. |
| [4] | Yang Lingyan, Li Xiaoguang, Chen Ying. A Sharp Threshold of Blow-Up of a Class of Schrödinger-Hartree Equations [J]. Acta mathematica scientia,Series A, 2016, 36(6): 1117-1123. |
| Viewed | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
Full text 213
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Abstract 223
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
Cited |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
| Shared | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Discussed | ||||||||||||||||||||||||||||||||||||||||||||||||||
|