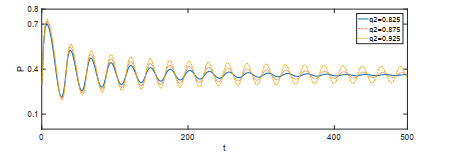
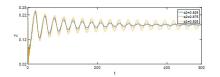
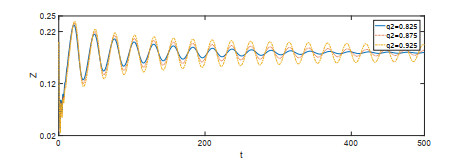
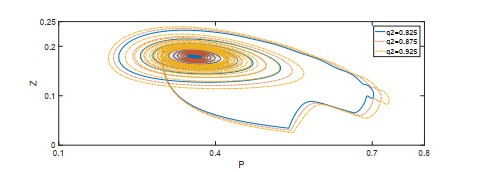
Acta mathematica scientia,Series A ›› 2022, Vol. 42 ›› Issue (2): 570-582.
Previous Articles Next Articles
Hopf Bifurcation for a Fractional Differential-Algebraic Predator-Prey System with Time Delay and Economic Profit
Daoxiang Zhang,Ben Li,Dandan Chen,Yating Lin,Xinmei Wang
- School of Mathematics and Statistics, Anhui Normal University, Wuhu Anhui 241002
-
Received:2020-11-30Online:2022-04-26Published:2022-04-18 -
Supported by:the NSFC(11671013);the NSFC(11302002);the NSF of Anhui Province(2008085MA13)
CLC Number:
- O175.1
Cite this article
Daoxiang Zhang,Ben Li,Dandan Chen,Yating Lin,Xinmei Wang. Hopf Bifurcation for a Fractional Differential-Algebraic Predator-Prey System with Time Delay and Economic Profit[J].Acta mathematica scientia,Series A, 2022, 42(2): 570-582.
share this article
| 1 |
Legendre L . The significance of microalgal blooms for fisheries and for the export of particulate organic carbon in oceans. Journal of Plankton Research, 1990, 12 (4): 681- 699
doi: 10.1093/plankt/12.4.681 |
| 2 | Liu X X , Huang Q D . The dynamics of a harvested predator-prey system with Holling type IV functional response. BioSystems, 2018, 169: 26- 39 |
| 3 |
Nosrati K , Shafiee M . Dynamic analysis of fractional-order singular Holling type-Ⅱ predator-prey system. Applied Mathematics and Computation, 2017, 313: 159- 179
doi: 10.1016/j.amc.2017.05.067 |
| 4 |
Scheffer M . Fish and nutrients interplay determines algal biomass: a minimal model. Oikos, 1991, 62: 271- 282
doi: 10.2307/3545491 |
| 5 |
Rihan F A , Anwar M N . Qualitative analysis of delayed SIR epidemic model with a saturated incidence rate. International Journal of Differential Equations, 2012,
doi: 10.1155/2012/408637 |
| 6 | Zhang D X , Sun G X , Zhao L X , Yan P . Pattern formation and selection in a diffusive predator-prey system with ratio-dependent functional response. Acta Ecologica Sinica, 2017, 38 (5): 290- 297 |
| 7 | Hillary R , Bees M . Plankton lattices and the role of chaos in plankton patchiness. Physical Review E, 2004, 69 (3): 1- 11 |
| 8 |
Han R J , Dai B X . Hopf bifurcation in a reaction-diffusive two-spcies model with nonlocal delay effect and general functional response. Chaos Solitons and Fractals, 2017, 96: 90- 109
doi: 10.1016/j.chaos.2016.12.022 |
| 9 | Rihan F A . Numerical modelling in biosciences using delay differential equations. Joural of Computational and Applied Mathematics, 2000, 125 (1/2): 183- 199 |
| 10 |
Zhang D X , Ding W W , Zhu M . Existence of positive periodic solutions of competitor-competitor-mutualist Lotka-Volterra systems with infinite delays. Journal of Systems Science and Complexity, 2015, 28 (2): 316- 326
doi: 10.1007/s11424-015-3128-y |
| 11 |
Rihan F A . Sensitivity analysis of dynamic systems with time lags. Joural of Computational and Applied Mathematics, 2003, 151 (2): 445- 462
doi: 10.1016/S0377-0427(02)00659-3 |
| 12 | Liao T C, Yu H G, Zhao M. Dynamics of delayed phytoplankton-zooplankton system with Crowley-Martin functional response. Advances in Difference Equations, 2017, 2017, Article number: 5 |
| 13 |
Crowley P H , Martin E K . Functional response and interference within and between year classes of a dragonfly population. Journal of the North American Benthological Society, 1989, 8 (3): 211- 221
doi: 10.2307/1467324 |
| 14 |
Zhao H Y , Zhang X B , Huang X X . Hopf bifurcation and spatial patterns of a delayed biological economic system with diffusion. Applied Mathematics and Computation, 2015, 266: 462- 480
doi: 10.1016/j.amc.2015.05.089 |
| 15 |
Battaglia J L , Cois O , Puigsegur L , Oustaloup A . Solving an inverse heat conduction problem using a non-integer identified model. International Journal of Heat and Mass Transf, 2001, 44 (14): 2671- 2680
doi: 10.1016/S0017-9310(00)00310-0 |
| 16 | Mainardi F. Fractional Calculus: Some Basic Problems in Continuum and Statistical Mechanics//Carpenteri A, Mainardi F. Fractals and Fractional Calculus in Continuum Mechanics. Wien: Springer, 1997: 291-348 |
| 17 | Hilfer R . Applications of Fractional Calculus in Physics. Singapore: World Scientific, 2000 |
| 18 |
Tlacuahuac A F , Biegler L T . Optimization of fractional order dynamic chemical processing systems. Industrial and Engineering Chemistry Research, 2014, 53 (13): 5110- 5127
doi: 10.1021/ie401317r |
| 19 |
Ahmed E , El-Sayed A M A , El-Saka H A . Equilibrium points, stability and numerical solutions of fractional-order predator-prey and rabies models. Journal of Mathematical Analysis and Applications, 2007, 325 (1): 542- 553
doi: 10.1016/j.jmaa.2006.01.087 |
| 20 |
Huang C D , Li H , Cao J D . A novel strategy of bifurcation control for a delayed fractional predator-prey model. Applied Mathematics and Computation, 2019, 347: 808- 838
doi: 10.1016/j.amc.2018.11.031 |
| 21 | Abdelouahab M S , Hamri N E , Wang J . Hopf bifurcation and chaos in fractional-order modified hybrid optical system. Nonlinear Dynamics, 2011, 69 (1/2): 275- 284 |
| 22 |
Gutierrez-Vega J C . Fractionalization of optical beams: I. Planar analysis. Optics Letters, 2007, 32 (11): 1521- 1523
doi: 10.1364/OL.32.001521 |
| 23 |
Li H , Zhang L , Hu C . Dynamic analysis of a fractional-order single-species model with diffusion. Nonlinear Analysis: Modelling and Control, 2017, 22 (3): 303- 316
doi: 10.15388/NA.2017.3.2 |
| 24 |
Gordon H . The economic theory of a common property resource: The fishery. Journal of Political Economy, 1954, 62: 124- 142
doi: 10.1086/257497 |
| 25 |
Zhang X , Zhang Q , Zhang Y . Bifurcations of a class of singular biological economic models. Chaos Solitons and Fractals, 2009, 40 (3): 1309- 1318
doi: 10.1016/j.chaos.2007.09.010 |
| 26 |
Zhang X , Zhang Q Q . Bifurcation analysis and control of a differential-algebraic predator-prey model with Allee effect and time delay. Journal of Applied Mathematics, 2014,
doi: 10.1155/2014/107565 |
| 27 |
Zhang G , Zhu L , Chen B . Hopf bifurcation and stability for a differential-algebraic biological economic system. Applied Mathematics and Computation, 2010, 217 (1): 330- 338
doi: 10.1016/j.amc.2010.05.065 |
| 28 |
El-Saka H A A , Lee S , Jang B . Dynamic analysis of fractional-order predator-prey biological economic system with Holling type Ⅱ functional response. Nonlinear Dynamics, 2019, 96: 407- 416
doi: 10.1007/s11071-019-04796-y |
| 29 |
Nosrati K , Shafiee M . Dynamic analysis of fractional-order singular Holling type-Ⅱ predator-prey system. Applied Mathematics and Computation, 2017, 313: 159- 179
doi: 10.1016/j.amc.2017.05.067 |
| [1] | Yue Sun,Daoxiang Zhang,Wen Zhou. The Influence of Fear Effect on Stability Interval of Reaction-Diffusion Predator-Prey System with Time Delay [J]. Acta mathematica scientia,Series A, 2021, 41(6): 1980-1992. |
| [2] | Jingnan Wang,Dezhong Yang. Stability and Bifurcation of a Pathogen-Immune Model with Delay and Diffusion Effects [J]. Acta mathematica scientia,Series A, 2021, 41(4): 1204-1217. |
| [3] | Xiling Li,Fei Gao,Wenqin Li. Stability Analysis of Fractional-Order Hepatitis B Virus Infection Model With Immune Delay [J]. Acta mathematica scientia,Series A, 2021, 41(2): 562-576. |
| [4] | Gaihui Guo,Xiaohui Liu. Hopf Bifurcation and Stability for an Autocatalytic Reversible Biochemical Reaction Model [J]. Acta mathematica scientia,Series A, 2021, 41(1): 166-177. |
| [5] | Jian Liu,Zhixin Zhang,Wei Jiang. Global Mittag-Leffler Stability of Fractional Order Nonlinear Impulsive Differential Systems with Time Delay [J]. Acta mathematica scientia,Series A, 2020, 40(4): 1053-1060. |
| [6] | Haiyin Li. Hopf Bifurcation of Delayed Density-Dependent Predator-Prey Model [J]. Acta mathematica scientia,Series A, 2019, 39(2): 358-371. |
| [7] | Lifei Zheng,Jie Guo,Meihua Wu,Xiaorui Wang,Aying Wan. The Research on a Class of the Predator-Prey-Mutualist System with Delays [J]. Acta mathematica scientia,Series A, 2018, 38(5): 1001-1013. |
| [8] | Yang Jihua, Zhang Erli, Liu Mei. Dynamic Analysis and Chaos Control of a Finance System with Delayed Feedbacks [J]. Acta mathematica scientia,Series A, 2017, 37(4): 767-782. |
| [9] | Zhou Jun. Turing Instability and Hopf Bifurcation of a Bimolecular Model with Autocatalysis and Saturation Law [J]. Acta mathematica scientia,Series A, 2017, 37(2): 366-373. |
| [10] | Wang Heyuan. The Dynamical Behaviors and the Numerical Simulation of a Five-Mode Lorenz-Like System of the MHD Equations for a Two-Dimensional Incompressible Fluid on a Torus [J]. Acta mathematica scientia,Series A, 2017, 37(1): 199-216. |
| [11] | Zhang Shuwen. A Stochastic Predator-Prey System with Time Delays and Prey Dispersal [J]. Acta mathematica scientia,Series A, 2015, 35(3): 592-603. |
| [12] | Luo Ricai, Xu Honglei, Wang Wusheng. Globally Asymptotic Stability of A New Class of Neutral Neural Networks with Time-Varying Delays [J]. Acta mathematica scientia,Series A, 2015, 35(3): 634-640. |
| [13] | Wan Aying, Yi Fengqi, Zheng Lifei. Hopf Bifurcation Analysis and Oscillatory Patterns of A Diffusive Gierer-Meinhardt Model [J]. Acta mathematica scientia,Series A, 2015, 35(2): 381-394. |
| [14] | WANG Xue-Chen, WEI Jun-Jie. The Effect of Delay on a Diffusive Predator-Prey System with Ivlev-Type Functional Response [J]. Acta mathematica scientia,Series A, 2014, 34(2): 234-250. |
| [15] | JIANG Yu, MEI Li-Quan, SONG Xin-Yu, TIAN Wei-Jun, DING Xue-Mei. Analysis of an Impulsive Epidemic Model with Time Delays and Nonlinear Incidence Rate [J]. Acta mathematica scientia,Series A, 2012, 32(4): 670-684. |
|