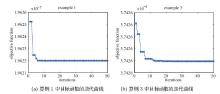
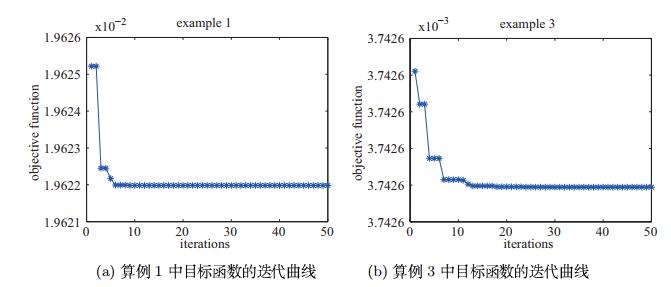
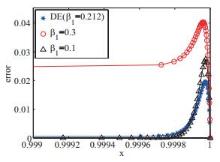
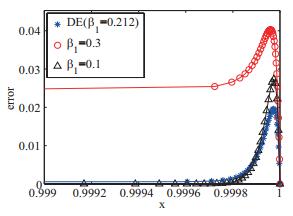
Acta mathematica scientia,Series A ›› 2021, Vol. 41 ›› Issue (1): 245-253.
Previous Articles Next Articles
Differential Evolution Algorithms for Boundary Layer Problems on Bakhvalov-Shishkin Mesh
- 1 School of Information, Mechanical and Electrical Engineering, Hunan International Economics University, Changsha 410205
2 MOE-LCSM, Hunan Normal University, Changsha 410081
-
Received:2019-07-23Online:2021-02-26Published:2021-01-29 -
Contact:Qin Zhou E-mail:19891881@qq.com -
Supported by:the NSFC(11771138);the Scientific Research Fund of Hunan Provincial Education Department(18C1097);the Scientific Research Fund of Hunan Provincial Education Department(19B325);the Provincial First-Class Undergraduate Course of Hunan Provinc(2019)
CLC Number:
- O241
Cite this article
Qin Zhou,Lizheng Cheng. Differential Evolution Algorithms for Boundary Layer Problems on Bakhvalov-Shishkin Mesh[J].Acta mathematica scientia,Series A, 2021, 41(1): 245-253.
share this article
"
| ε | N = 32 | N = 64 | N = 128 | N = 256 | ||||
| 误差 | β1 | 误差 | β1 | 误差 | β1 | 误差 | β1 | |
| 10-2 | 3.337E-02 | 0.269 | 1.766E-02 | 0.278 | 9.068E-03 | 0.296 | 4.589E-03 | 0.293 |
| 10-3 | 3.578E-02 | 0.213 | 1.861E-02 | 0.255 | 9.468E-03 | 0.279 | 4.774E-03 | 0.282 |
| 10-4 | 3.664E-02 | 0.211 | 1.896E-02 | 0.245 | 9.577E-03 | 0.265 | 4.808E-03 | 0.275 |
| 10-5 | 3.839E-02 | 0.173 | 1.962E-02 | 0.212 | 9.778E-03 | 0.238 | 4.857E-03 | 0.261 |
| 10-6 | 4.023E-02 | 0.156 | 2.062E-02 | 0.183 | 1.017E-02 | 0.211 | 4.986E-03 | 0.234 |
"
| ε | N = 32 | N = 64 | N = 128 | N = 256 | ||||
| 误差 | β1 | 误差 | β1 | 误差 | β1 | 误差 | β1 | |
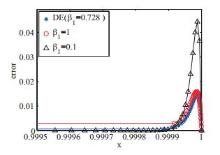
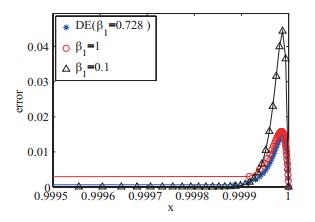
| 10-2 | 2.646E-02 | 0.842 | 1.403E-02 | 0.797 | 7.218E-03 | 0.837 | 3.657E-03 | 0.826 |
| 10-3 | 2.790E-02 | 0.711 | 1.463E-02 | 0.729 | 7.447E-03 | 0.769 | 3.749E-03 | 0.806 |
| 10-4 | 2.808E-02 | 0.710 | 1.471E-02 | 0.728 | 7.483E-03 | 0.768 | 3.765E-03 | 0.790 |
| 10-5 | 2.810E-02 | 0.709 | 1.472E-02 | 0.728 | 7.487E-03 | 0.768 | 3.766E-03 | 0.790 |
| 10-6 | 2.810E-02 | 0.709 | 1.472E-02 | 0.728 | 7.487E-03 | 0.768 | 3.767E-03 | 0.790 |
"
| ε | N = 32 | N = 64 | N = 128 | N = 256 | ||||
| 误差 | β2 | 误差 | β2 | 误差 | β2 | 误差 | β2 | |
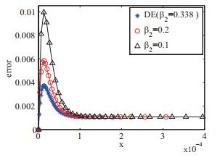
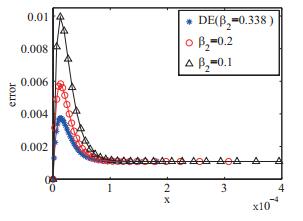
| 10-2 | 5.773E-03 | 0.441 | 2.879E-03 | 0.446 | 1.393E-03 | 0.430 | 6.534E-04 | 0.397 |
| 10-3 | 6.997E-03 | 0.345 | 3.638E-03 | 0.357 | 1.851E-03 | 0.364 | 9.320E-04 | 0.368 |
| 10-4 | 7.154E-03 | 0.330 | 3.733E-03 | 0.340 | 1.907E-03 | 0.346 | 9.636E-04 | 0.350 |
| 10-5 | 7.172E-03 | 0.328 | 3.743E-03 | 0.338 | 1.913E-03 | 0.344 | 9.670E-04 | 0.347 |
| 10-6 | 7.173E-03 | 0.328 | 3.744E-03 | 0.338 | 1.914E-03 | 0.344 | 9.673E-04 | 0.347 |
| 1 |
Linβ T . Layer-adapted meshes for convection-diffusion problems. Comput Methods Appl Mech Engrg, 2003, 192: 1061- 1105
doi: 10.1016/S0045-7825(02)00630-8 |
| 2 |
Zahra W K , Van D M . Discrete spline solution of singularly perturbed problem with two small parameters on a Shishkin-type mesh. Computational Mathematics and Modeling, 2018, 29 (3): 367- 381
doi: 10.1007/s10598-018-9416-3 |
| 3 |
Brdar M , Zarin H . A singularly perturbed problem with two parameters on a Bakhvalov-type mesh. Journal of Computational and Applied Mathematics, 2016, 292: 307- 319
doi: 10.1016/j.cam.2015.07.011 |
| 4 | Cen Z , Chen J , Xi L . A second-order hybrid finite difference scheme for a system of coupled singularly perturbed initial value problems. Journal of Computational and Applied Mathematics, 2010, 234 (12): 3445- 3457 |
| 5 |
周琴, 杨银. 求解二阶双曲型方程的自适应网格方法. 数学物理学报, 2019, 39A (4): 942- 950
doi: 10.3969/j.issn.1003-3998.2019.04.021 |
|
Zhou Q , Yang Y . Adaptive mesh method for solving a second-order hyperbolic equation. Acta Math Sci, 2019, 39A (4): 942- 950
doi: 10.3969/j.issn.1003-3998.2019.04.021 |
|
| 6 |
Linβ T , Radojev G , Zarin H . Approximation of singularly perturbed reaction-diffusion problems by quadratic-splines. Numerical Algorithms, 2012, 61 (1): 35- 55
doi: 10.1007/s11075-011-9529-7 |
| 7 |
Shakti D , Mohapatra J . Layer-adapted meshes for parameterized singular perturbation problem. Procedia Engineering, 2015, 127: 539- 544
doi: 10.1016/j.proeng.2015.11.342 |
| 8 | Yang J M . Improved uniform convergence of a finite difference approximation to a kind of singularly perturbed problems. Journal of Zhejiang University (Science Edition), 2013, 40 (2): 136- 139 |
| 9 | Chen Y P . Uniform convergence analysis of finite difference approximations for singular perturbation problems on an adapted grid. Advances in Computational Mathematics, 2006, 24 (1): 197- 212 |
| 10 |
Zhou Q , Chen Y P , Yang Y . Two improved algorithms and implementation for a singularly perturbed problem on moving meshes. Journal of Systems Science and Complexity, 2011, 24 (6): 1232- 1240
doi: 10.1007/s11424-011-8138-9 |
| 11 | Yin Y , Zhu P , Wang B . Analysis of a streamline-diffusion finite element method on Bakhvalov-Shishkin mesh for singularly perturbed problem. Numerical Mathematics:Theory, Methods and Applications, 2017, 10 (1): 44- 64 |
| 12 |
Roos H G , Linβ T . Sufficient conditions for uniform convergence on layer-adapted grids. Computing, 1999, 63 (1): 27- 45
doi: 10.1007/s006070050049 |
| 13 | 周琴. 一类奇异摄动问题差分格式的一致收敛性分析. 湖南工程学院学报(自然科学版), 2009, 19 (3): 34- 36 |
| Zhou Q . Analysis of uniform convergence for difference scheme of a singularly perturbed problem. Journal of Hunan Institute of Engineering(Natural Science Edition), 2009, 19 (3): 34- 36 | |
| 14 | 江山, 孙美玲. 多尺度有限元结合Bakhvalov-Shishkin网格法高效处理边界层问题的研究. 浙江大学学报(理学版), 2015, 42 (2): 142- 146 |
| Jiang S , Sun M L . Combining the multiscale finite element and Bakhvalov-Shishkin grid to solve the boundary layer problems. Journal of Zhejiang University(Science Edition), 2015, 42 (2): 142- 146 | |
| 15 | Storn R , Price K . Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces. Journal of Global Optimization, 1997, 11 (4): 341- 359 |
| 16 | 魏文红, 王甲海, 陶铭. 基于泛化反向学习的多目标约束差分进化算法. 计算机研究与发展, 2016, 53 (6): 1410- 1421 |
| Wei W H , Wang J H , Tao M . Multi-objective constrained differential evolution using generalized opposition-based learning. Journal of Computer Research and Development, 2016, 53 (6): 1410- 1421 | |
| 17 | 朱李楠, 王万良, 沈国江. 基于改进差分进化算法的云制造资源优化组合方法. 计算机集成制造系统, 2017, 1: 203- 214 |
| Zhu L N , Wang W L , Shen G J . Resource optimization combination method based on improved differential evolution algorithm for cloud manufacturing. Computer Integrated Manufacturing Systems, 2017, 1: 203- 214 | |
| 18 | 刘利斌, 隆广庆, 上官珍萍. 差分进化与有理谱方法求解奇异摄动问题. 计算机工程与应用, 2018, 54 (17): 225- 230 |
| Liu L B , Long G Q , Shangguan Z P . Differential evolution and rational spectral methods for singularly perturbed problems. Computer Engineering and Applications, 2018, 54 (17): 225- 230 |
| [1] | Limeng Wu,Mingkang Ni,Suhong Li,Haibo Lu. Asymptotic Solution of Singularly Perturbed Boundary Value Problem with Integral Boundary Condition [J]. Acta mathematica scientia,Series A, 2020, 40(5): 1192-1203. |
| [2] | Na Wang,Shu Wang. The Boundary Layer for MHD Equations in a Plane-Parallel Channel [J]. Acta mathematica scientia,Series A, 2019, 39(4): 738-760. |
| [3] | Huaxiong Chen,Yanyan Wang,Mingkang Ni. The Contrast Structure for the Singularly Perturbed Problem with Slow-Fast Layers and Discontinuous Righthand Side [J]. Acta mathematica scientia,Series A, 2019, 39(4): 865-874. |
| [4] | YANG Yu-Bo, ZHU Peng, YIN Yun-Hui. A Optimal Uniformly Convergent Discontinuous Galerkin Finite Element Method for Singularly Perturbed Problem [J]. Acta mathematica scientia,Series A, 2014, 34(3): 716-726. |
| [5] | Chen Qiong; Xiang Zhaoyin; Mu Chunlai. Blow-up Profiles to a Nonlocal Reaction-diffusion System [J]. Acta mathematica scientia,Series A, 2007, 27(3): 420-427. |
| [6] | MO Jia-Qi, HAN Xiang-Lin. Asymptotic Shock Solution for a Nonlinear Equation [J]. Acta mathematica scientia,Series A, 2004, 24(2): 164-167. |
| [7] | MO Jia-Qi. A Class of Shock Solution for Nonlinear Equations [J]. Acta mathematica scientia,Series A, 2003, 23(5): 530-534. |
| [8] | HAN Xiang-Lin. The Shock Solution for a Class of Nonlinear Equation [J]. Acta mathematica scientia,Series A, 2003, 23(2): 253-256. |
|