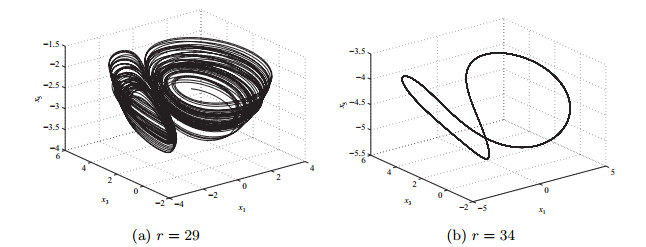
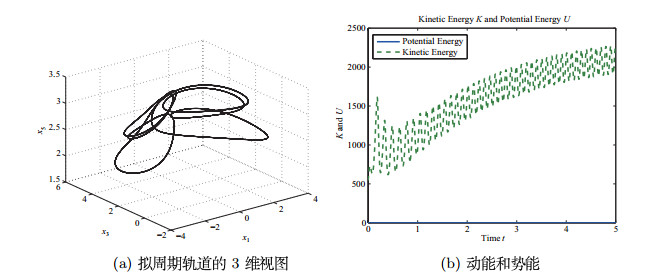
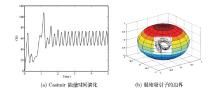
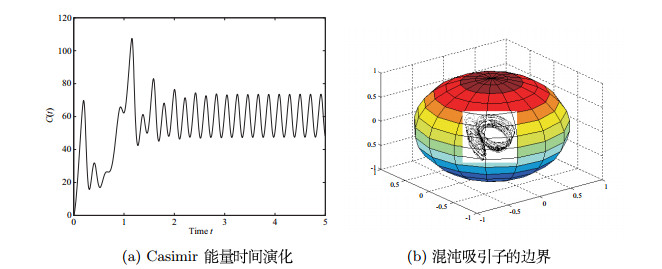
Acta mathematica scientia,Series A ›› 2020, Vol. 40 ›› Issue (2): 315-327.
Previous Articles Next Articles
Dynamical Mechanism and Energy Evolution of a Five-Modes System of the Navier-Stokes Equations For a Two-Dimensional Incompressible Fluid on a Torus
- 1 College of Mathematics and Systematics Sciences, Shenyang Normal University, Shenyang 110034
2 College of Sciences, Liaoning University of Technology, Liaoning Jin'zhou 121001
-
Received:2018-04-11Online:2020-04-26Published:2020-05-21 -
Supported by:the NSFC(11572146);the Doctor Science Foundation of Shenyang Normal University(054-91900302009)
CLC Number:
- O175.1
Cite this article
Heyuan Wang. Dynamical Mechanism and Energy Evolution of a Five-Modes System of the Navier-Stokes Equations For a Two-Dimensional Incompressible Fluid on a Torus[J].Acta mathematica scientia,Series A, 2020, 40(2): 315-327.
share this article
"
0 | |||||
| 定点 | 稳定结点 | 鞍结点(一个方向不稳,另两个方向稳定) | |||
| 定点 | 不存在 | 稳定结点 | 稳定焦点 | 稳定焦点 | 鞍点 |
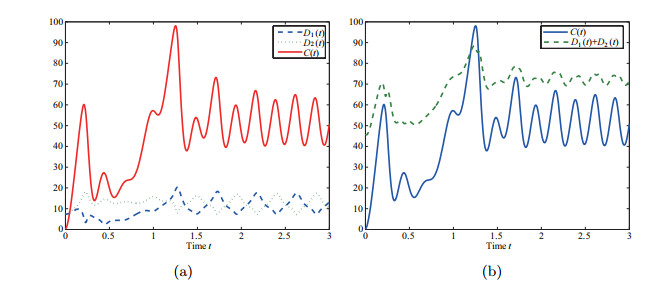
| 系统(2.1)相空间中的运动情况 | 趋于稳定定态 | 趋于稳定定态 | 运动最终按螺旋线趋于 | 同左,但越靠近 | 不稳定极限环(亚临界霍普夫分岔) |
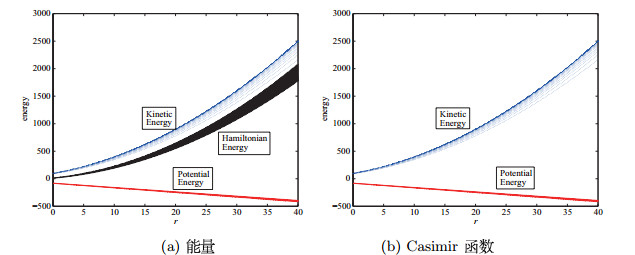
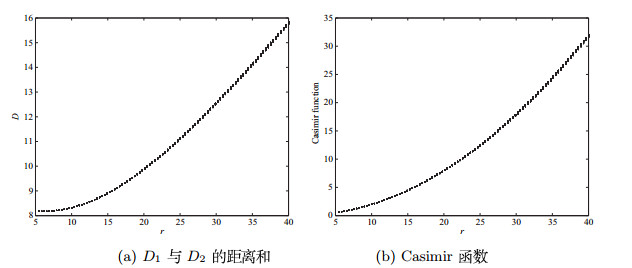
| 动能 | 最小值 | 逐渐增大 | 保持增大 | 增长 | |
| Casimir函数 | 最小值 | 逐渐增大 | 保持增大 | 增长 | |
| 不存在 | 逐渐递增 | 递增增大 | 逐渐 | ||
| 1 |
Lorenz N E . Deterministic nonperiodic flow. Journal of the Atmospheric Sciences, 1963, 20, 130- 141
doi: 10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2 |
| 2 | Teman R. Infinite Dimensional Dynamic System in Mechanics and Physics. New York: Springer-Verlog, 2000 |
| 3 |
Pchelintsev A N . Numerical and physical modeling of the dynamics of the lorenz system. Numerical Analysis and Applications, 2014, 7 (2): 159- 167
doi: 10.1134/S1995423914020098 |
| 4 |
Boldrighini C , Franceschini V . A five-dimensional truncation of the plane incompressible Navier-Stokes equations. Communications in Mathematical Physics, 1979, 64, 159- 170
doi: 10.1007/BF01197511 |
| 5 | Sparrow C. The Lorenz Equations: Bifurcations, Chaos, and Strange Attractors. New York: Springer Verlag, 1982 |
| 6 | Franceschini V , Tebaldi C . A seven-modes truncation of the plane incompressible Navier-Stokes equations. Journal of Statistical Physics, 1981, 25 (3): 397- 417 |
| 7 | Hilborn R C . Chaos and Nonlinear Dynamics. Landon: Oxford Univ Press, 1994 |
| 8 | Franceschini V , Inglese G , Tebaldi C . A five-mode truncation of the Navier-Stokes equations on a three-dimensional torus. Commun Mech Phys, 1988, 64, 35- 40 |
| 9 |
Leonov G A , Kuznetsov N V , Korzhemanova N A , Kusakin D V . Lyapunov dimension formula for the global attractor of the Lorenz system. Communications in Nonlinear Science and Numerical Simulation, 2016, 41, 84- 103
doi: 10.1016/j.cnsns.2016.04.032 |
| 10 |
Leonov G A , Kuznetsov N V . On differences and similarities in the analysis of Lorenz, Chen, and Lu systems. Applied Mathematics and Computation, 2015, 256, 334- 343
doi: 10.1016/j.amc.2014.12.132 |
| 11 | Franceschini V , Zanasi R . Three-dimensional Navier-Stokes equations trancated on a torus. Nonlinearity, 1992, 4, 189- 209 |
| 12 |
Franceschini V , Tebaldi C . Breaking and disappearance of tori. Commun Math Phys, 1984, 94, 317- 329
doi: 10.1007/BF01224828 |
| 13 | Arnold V . Kolmogorov's hydrodynamic attractors. Proc R Soc Lond A, 1991, 434 (19): 19- 22 |
| 14 |
Pasini A , Pelino V , Potesta S . Torsion and attractors in the Kolmogorov hydrodynamical system. Phys Lett A, 1998, 241, 77- 83
doi: 10.1016/S0375-9601(98)00113-3 |
| 15 |
Pasini A , Pelino V . A unified view of Kolmogorov and Lorenz systems. Phys Lett A, 2000, 275, 435- 446
doi: 10.1016/S0375-9601(00)00620-4 |
| 16 |
Pelino V , Pasini A . Dissipation in Lie-Poisson systems and the Lorenz-84 model. Phys Lett A, 2001, 291, 389- 396
doi: 10.1016/S0375-9601(01)00764-2 |
| 17 | Liang X Y , Qi G Y . Mechanical analysis and energy conversion of Chen chaotic system. General and Applied Physics, 2017, 47 (4): 288- 294 |
| 18 |
Liang X Y , Qi G Y . Mechanical analysis of Chen chaotic system. Chaos, Solitons and Fractals, 2017, 98, 173- 177
doi: 10.1016/j.chaos.2017.03.021 |
| 19 |
Qi G , Liang X . Mechanical analysis of Qi four-wing chaotic system. Nonlinear Dyn, 2016, 86 (2): 1095- 1106
doi: 10.1007/s11071-016-2949-0 |
| 20 |
Pelino V , Maimone F , Pasini A . Energy cycle for the Lorenz attractor. Chaos Soliton Fract, 2014, 64, 67- 77
doi: 10.1016/j.chaos.2013.09.005 |
| 21 | Marsden J, Ratiu T. Introduction to Mechanics and Symmetry: A Basic Exposition of Classical Mechanical Systems. Berlin: Springer, 2002 |
| 22 | Strogatz S H. Nonlinear Dynamics and Chaos. Reading, MA: Addison-Wesley, 1994 |
| 23 | Morrison P J . Thoughts on brackets and dissipation:old and new. Journal of Physics:Conference Series, 2009, 169 (1): 012006 |
| 24 | Doering C R , Gibbon J D . On the shape and dimension of the Lorenz attractor. Dyn Stab Syst, 1995, 10 (3): 255 |
| [1] | Yongjian Liu,Qiujian Huang. Jacobi Analysis of the Rabinovich System [J]. Acta mathematica scientia,Series A, 2021, 41(3): 783-796. |
| [2] | Liheng Sang,Zhenlong Chen,Xiaozhen Hao. Smoothness for the Renormalized Self-Intersection Local Time of Bifractional Brownian Motion [J]. Acta mathematica scientia,Series A, 2020, 40(3): 796-810. |
| [3] | Heyuan Wang. Dynamical Mechanism and Energy Conversion of Couette-Taylor Flow [J]. Acta mathematica scientia,Series A, 2020, 40(1): 243-256. |
| [4] | Zhi Wang,Litan Yan,Xianye Yu. Local Times of the Solution to Stochastic Heat Equation with Fractional Noise [J]. Acta mathematica scientia,Series A, 2019, 39(3): 582-595. |
| [5] | Wang Jianjun. On the Invariance of Maximal Distributional Chaos of Weighted Shift Operators on ∑(X) [J]. Acta mathematica scientia,Series A, 2018, 38(3): 446-453. |
| [6] | Yao Yuwu, Chen Xiu, Niu Xin. Distributional Chaos on Complex Sectors [J]. Acta mathematica scientia,Series A, 2017, 37(5): 950-961. |
| [7] | Wu Xinxing. A Remark on the Weak Specification Property [J]. Acta mathematica scientia,Series A, 2017, 37(4): 601-606. |
| [8] | Yang Jihua, Zhang Erli, Liu Mei. Dynamic Analysis and Chaos Control of a Finance System with Delayed Feedbacks [J]. Acta mathematica scientia,Series A, 2017, 37(4): 767-782. |
| [9] | Wang Heyuan, Cui Jin. The Analysis of Global Stability and Numerical Simulation of Chaos Behaviors of Rotating Flow [J]. Acta mathematica scientia,Series A, 2017, 37(4): 783-792. |
| [10] | Wang Heyuan. The Dynamical Behaviors and the Numerical Simulation of a Five-Mode Lorenz-Like System of the MHD Equations for a Two-Dimensional Incompressible Fluid on a Torus [J]. Acta mathematica scientia,Series A, 2017, 37(1): 199-216. |
| [11] | Wu Xinxing, Wang Jianjun. Some Remarks on P-Minimal Dynamical Systems [J]. Acta mathematica scientia,Series A, 2016, 36(5): 879-885. |
| [12] | Lu Tianxiu, Zhu Peiyong, Wu Xinxing. Distributional Chaos in Nonautonomous Discrete Systems [J]. Acta mathematica scientia,Series A, 2015, 35(3): 558-566. |
| [13] | HU Han-Ping, LIU Shuang-Hong, WANG Zu-Xi, Wu Xiao-Gang. A Chaotic Poly phase Pseudorandom Sequence [J]. Acta mathematica scientia,Series A, 2004, 24(2): 251-256. |
| [14] | Zhang Jianfeng, Xie Xiangdong. Weak Transverse and Weak Chaos [J]. Acta mathematica scientia,Series A, 1998, 18(3): 241-245. |
| [15] | He Lianfa, Zhang Zhenguo. Chaos in the Semi-Flows and its Inverse Limit systems [J]. Acta mathematica scientia,Series A, 1997, 17(S1): 46-51. |
|