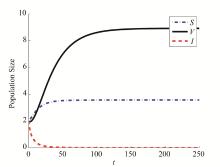
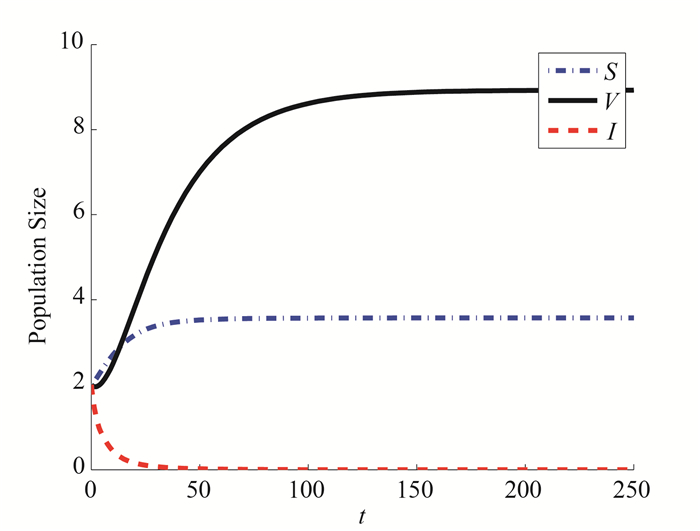
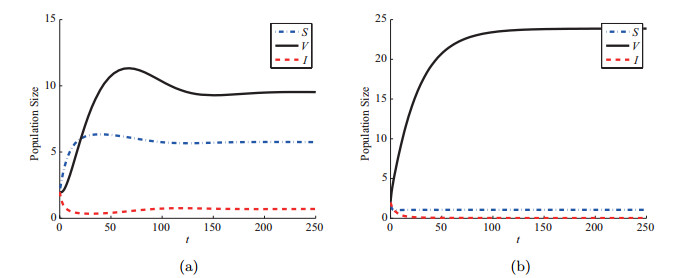
| 1 |
Buonomo B , Lacitignola D , Vargas-De-León C . Qualitative analysis and optimal control of an epidemic model with vaccination and treatment. Mathematics and Computers in Simulation, 2014, 100: 88- 102
doi: 10.1016/j.matcom.2013.11.005
|
| 2 |
Diekmann O , Heesterbeek J A , Metz J A . On the definition and the computation of the basic reproduction ratio R0 in models for infectious diseases in heterogeneous populations. Journal of Mathematical Biology, 1990, 28: 365- 382
|
| 3 |
Gumel A B , Moghadas S M . A qualitative study of a vaccination model with nonlinear incidence. Applied Mathematics and Computation, 2003, 143: 409- 419
doi: 10.1016/S0096-3003(02)00372-7
|
| 4 |
Gao D P , Huang N J , Kang S M , Zhang C . Global stability analysis of an SVEIR epidemic model with general incidence rate. Boundary Value Problems, 2008, 2008: 42
|
| 5 |
Huang G , Takeuchi Y , Ma W B , Wei D . Global stability for delay SIR and SEIR epidemic models with nonlinear incidence rate. Bulletin of Mathematical Biology, 2010, 72: 1192- 1207
doi: 10.1007/s11538-009-9487-6
|
| 6 |
Huang G , Ma W B , Takeuchi Y . Global properties for virus dynamics model with Beddington-DeAngelis functional response. Applied Mathematics Letters, 2006, 22: 1690- 1693
|
| 7 |
Hale J K , Waltman P . Persistence in infinite-dimensional systems. Society for Industrial and Applied Mathematics, 1989, 20: 388- 395
|
| 8 |
Kuniya T . Global stability of a multi-group SVIR epidemic model. Nonlinear Analysis:Real World Applications, 2013, 14 (2): 1135- 1143
doi: 10.1016/j.nonrwa.2012.09.004
|
| 9 |
Liu S Q , Wang S K , Wang L . Global dynamics of delay epidemic models with nonlinear incidence rate and relapse. Nonlinear Analysis:Real World Applications, 2011, 12: 119- 127
doi: 10.1016/j.nonrwa.2010.06.001
|
| 10 |
Liu W M , Hethcote H W , Levin S A . Dynamical behavior of epidemiological models with nonlinear incidence rates. Journal of Mathematical Biology, 1987, 25: 359- 380
doi: 10.1007/BF00277162
|
| 11 |
Liu X , Takeuchi Y , Iwami S . SVIR epidemic models with vaccination strategies. Journal of Theoretical Biology, 2008, 253 (1): 1- 11
|
| 12 |
Rost G , Wu J . Seir epidemiological model with varying infectivity and infinite delay. Mathematical Biosciences and Engineering, 2017, 5: 389- 402
|
| 13 |
Wang J L , Zhang R , Kuniya T . The stability analysis of an SVEIR model with continuous age-structure in the exposed and infectious classes. Journal of Biological Dynamics, 2015, 9: 73- 101
doi: 10.1080/17513758.2015.1006696
|
| 14 |
Wang J L . Sveir epidemiological model with varying infectivity and distributed delays. Mathematical Biosciences and Engineering, 2012, 8: 875- 888
|
| 15 |
Wang J L , Dong X , Sun H Q . Analysis of an SVEIR model with age-dependence vaccination, latency and relapse. Journal of Nonlinear Sciences and Application, 2017, 10 (7): 3755- 3776
doi: 10.22436/jnsa.010.07.31
|
| 16 |
Wang L W , Liu Z J , Zhang X A . Global dynamics for an age-structured epidemic model with media impact and incomplete vaccination. Nonlinear Analysis:Real World Applications, 2016, 32: 136- 158
doi: 10.1016/j.nonrwa.2016.04.009
|
| 17 |
Yamada K , Yoshimura M . A possible association of Y chromosome heterochromatin with stature. Human Genetics, 1981, 58 (3): 268- 270
doi: 10.1007/BF00294920
|
| 18 |
Zhang T L , Teng Z D . Global behavior and permanence of SIRS epidemic model with time delay. Nonlinear Analysis:Real World Applications, 2008, 9: 1409- 1424
doi: 10.1016/j.nonrwa.2007.03.010
|
 )
)