Acta mathematica scientia,Series A ›› 2019, Vol. 39 ›› Issue (5): 1228-1246.
Previous Articles Next Articles
System Capacity Optimization Design and Optimal Control Policy (N*, D*) for M/G/1 Queue with p-Entering Discipline and Min(N, D, V)-Policy
- 1 Nanchong Vocational & Technical College, Sichuan Nanchong 637000
2 School of Fundamental Education, Sichuan Normal University, Chengdu 610068
3 School of Mathematical Sciences, Sichuan Normal University, Chengdu 610068
-
Received:2018-10-23Online:2019-10-26Published:2019-11-08 -
Contact:Yinghui Tang E-mail:tangyh@sicnu.edu.cn -
Supported by:the NSFC(71571127)
CLC Number:
- O121
Cite this article
Le Luo,Yinghui Tang. System Capacity Optimization Design and Optimal Control Policy (N*, D*) for M/G/1 Queue with p-Entering Discipline and Min(N, D, V)-Policy[J].Acta mathematica scientia,Series A, 2019, 39(5): 1228-1246.
share this article
"
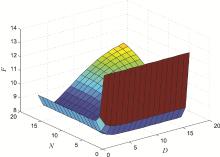
| DN |  |  |  |  |  |  |
| 1 | 13.144737 | 9.991536 | 9.563765 | 9.521530 | 9.523348 | 9.525169 |
| 2 | 13.144737 | 9.312163 | 8.666641 | 8.606744 | 8.641893 | 8.668439 |
| 3 | 13.144737 | 9.098830 | 8.356363 | 8.300900 | 8.391288 | 8.474396 |
| 4 | 13.144737 | 9.024516 | 8.235207 | 8.184978 | 8.325796 | 8.476696 |
| 5 | 13.144737 | 8.997709 | 8.185816 | 8.138259 | 8.315510 | 8.527172 |
| 6 | 13.144737 | 8.987918 | 8.165466 | 8.118911 | 8.319459 | 8.577624 |
| 7 | 13.144737 | 8.984325 | 8.157101 | 8.110828 | 8.325154 | 8.615477 |
| 8 | 13.144737 | 8.983005 | 8.153686 | 8.107553 | 8.329470 | 8.640445 |
| 9 | 13.144737 | 8.982519 | 8.152304 | 8.106051 | 8.332170 | 8.655647 |
| 10 | 13.144737 | 8.982304 | 8.151748 | 8.105571 | 8.333699 | 8.664381 |
| 11 | 13.144737 | 8.982275 | 8.151526 | 8.105234 | 8.334510 | 8.669176 |
| 12 | 13.144737 | 8.982251 | 8.151438 | 8.105137 | 8.334921 | 8.671714 |
| 13 | 13.144737 | 8.982242 | 8.151404 | 8.105097 | 8.335123 | 8.673016 |
| 14 | 13.144737 | 8.982239 | 8.151390 | 8.105082 | 8.335298 | 8.673667 |
| 15 | 13.144737 | 8.982237 | 8.151385 | 8.105075 | 8.335265 | 8.673985 |
| 16 | 13.144737 | 8.982237 | 8.151383 | 8.105073 | 8.335285 | 8.674137 |
| 17 | 13.144737 | 8.982237 | 8.151382 | 8.105072 | 8.335294 | 8.674209 |
| 17.3 | 13.144737 | 8.982237 | 8.151382 | 8.105072 | 8.335296 | 8.674222 |
| 17.4 | 13.144737 | 8.982237 | 8.151382 |          | 8.335296 | 8.674226 |
| 17.5 | 13.144737 | 8.982237 | 8.151382 | 8.105071 | 8.335297 | 8.674229 |
| 18 | 13.144737 | 8.982237 | 8.151382 | 8.105071 | 8.335298 | 8.674243 |
| 19 | 13.144737 | 8.982237 | 8.151381 | 8.105071 | 8.335300 | 8.674258 |
| 20 | 13.144737 | 8.982237 | 8.151381 | 8.105071 | 8.335301 | 8.674265 |
| 1 |
Yadin M , Naor P . Queueing system with a removable service station. Operation Research Quarterly, 1963, 14 (4): 393- 405
doi: 10.1057/jors.1963.63 |
| 2 | Balachandran K . Control policies for a single server system. Management Science, 1973, 19 (4): 1013- 1018 |
| 3 |
Heyman D P .       doi: 10.1287/mnsc.23.7.775 |
| 4 |
Doshi B . Queueing systems with vacations-A survey. Queueing Systems, 1986, 1: 29- 66
doi: 10.1007/BF01149327 |
| 5 |
Ke J C . Modified       doi: 10.1016/j.mcm.2004.08.009 |
| 6 |
Lee H W , Beak J W , Jeon J . Analysis of the        doi: 10.1081/SAP-200064479 |
| 7 |
Wang K H , Kuo C C , Ke J C . Optical control of the       doi: 10.3844/ajassp.2008.565.573 |
| 8 |
Lan S J , Tang Y H . Analysis of         doi: 10.1051/ro/2016006 |
| 9 |
Tang Y H , Tang X W . The queue-length distribution for       |
| 10 |
骆川义, 唐应辉, 刘仁彬. 多级适应性休假      doi: 10.3969/j.issn.1000-0577.2007.06.011 |
Luo C Y , Tang Y H , Liu R B . The queue length distribution of       doi: 10.3969/j.issn.1000-0577.2007.06.011 |
|
| 11 |
Tang Y H . The departure process of the      doi: 10.2307/3215330 |
| 12 | Tang Y H , Yun X , Huang S J . Discrete-time queue with unreliable server and multiple adaptive delayed vacation. J of Computational and Applied Mathematics, 2008, 220 (3): 439- 455 |
| 13 |
Yu M M , Tang Y H , Fu Y H , Pan L M .              doi: 10.1016/j.cam.2010.10.013 |
| 14 |
Luo C Y , Tang Y H . The recursive solution for               doi: 10.1007/s10255-011-0049-y |
| 15 |
Luo C Y , Tang Y H , Chao B S , Xiang K L . Performance analysis of a discrete-time        doi: 10.1016/j.apm.2013.01.033 |
| 16 |
Lan S J , Tang Y H , Yu M M . System capacity optimization design and optimal threshold                  |
| 17 |
Gu J X , Wei Y Y , Tang Y H , Yu M M . Queue size distribution of                doi: 10.1007/s11424-016-4180-y |
| 18 |
井彩霞, 崔颖, 田乃硕.              doi: 10.3969/j.issn.1007-3221.2006.03.011 |
Jing C X , Cui Y , Tian N S . Analysis of the              doi: 10.3969/j.issn.1007-3221.2006.03.011 |
|
| 19 |
唐应辉, 吴文青, 刘云颇, 刘晓云. 基于多重休假的             |
Tang Y H , Wu W Q , Liu Y P , Liu X Y . The queue length distribution of              |
|
| 20 |
唐应辉, 吴文青, 刘云颇. 基于单重休假的             |
Tang Y H , Wu W Q , Liu Y P . Analysis of              |
|
| 21 |
蒋书丽, 唐应辉. 具有多级适应性休假和             |
Jiang S L , Tang Y H .              |
|
| 22 |
高丽君, 唐应辉. 具有             |
Gao L J , Tang Y H .              |
|
| 23 |
蔡晓丽, 唐应辉. 具有温储备失效特征和单重休假             |
Cai X L , Tang Y H .              |
|
| 24 |
Lee H W , Seo W J . The performance of the              doi: 10.1016/j.peva.2008.04.006 |
| 25 |
Lee H W , Seo W J , Lee S W , Jeon J . Analysis of the                doi: 10.1080/15326340903517121 |
| 26 |
魏瑛源, 唐应辉, 等. 基于             |
Wei Y Y , Tang Y H , et al. Queue length distribution and optimum policy for              |
|
| 27 |
罗乐, 唐应辉. 具有               |
Luo L , Tang Y H .                |
|
| 28 |
王敏, 唐应辉. 基于               |
Wang M , Tang Y H . Optimal control policy of                |
|
| 29 |
唐应辉, 毛勇. 服务员假期中以概率      |
Tang Y H , Mao Y . The stochastic decomposition for       |
|
| 30 |
骆川义, 唐应辉. 假期中以概率      |
Luo C Y , Tang Y H . The       |
|
| 31 |
李才良, 唐应辉, 牟永聪, 等. 在第二类故障期间以概率      |
Li C L , Tang Y H , Mu Y C , et al.       |
|
| 32 |
刘云颇, 唐应辉. 多重假期中以概率      |
Liu Y P , Tang Y H .       |
|
| 33 |
骆川义, 唐应辉. 具有可变到达率的多重休假            |
Luo C Y , Tang Y H . Analysis of a multi-vacation             |
|
| 34 |
Luo C Y , Xiang K L , Yu M M , Tang Y H . Recursive solution of queue length distribution for        doi: 10.1016/j.camwa.2011.02.018 |
| 35 |
Wei Y Y , Yu M M , Tang Y Y , Gu J X . Queue size distribution and capacity optimum design for                 |
| 36 |
Luo C Y , Tang Y H , Yu K Z , Ding C . Optimal             |
| 37 |
Lan S J , Tang Y H . Analysis of a discrete-time               |
| 38 | 唐应辉, 唐小我. 排队论-基础与分析技术. 北京: 科学出版社, 2006 |
| Tang Y H , Tang X W . Queueing Theory-Foundations and Analysis Techniques. Beijing: Science Press, 2006 |
| [1] | Quyu Pan,Yinghui Tang. Analysis of M/G/1 Repairable Queueing System and Optimal Control Policy with a Replaceable Repair Facility Under Delay Min(N, D)-Policy [J]. Acta mathematica scientia,Series A, 2018, 38(5): 1014-1031. |
| [2] | Gao Lijun, Tang Yinghui. M/G/1 Repairable Queueing System and Optimal Control Policy with Min(N,D)-Policy [J]. Acta mathematica scientia,Series A, 2017, 37(2): 352-365. |
| Viewed | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
Full text 125
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Abstract 128
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
Cited |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
| Shared | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Discussed | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
||