非凸非光滑优化问题的两步惯性 Bregman 邻近交替线性极小化算法

摘要/Abstract

摘要：

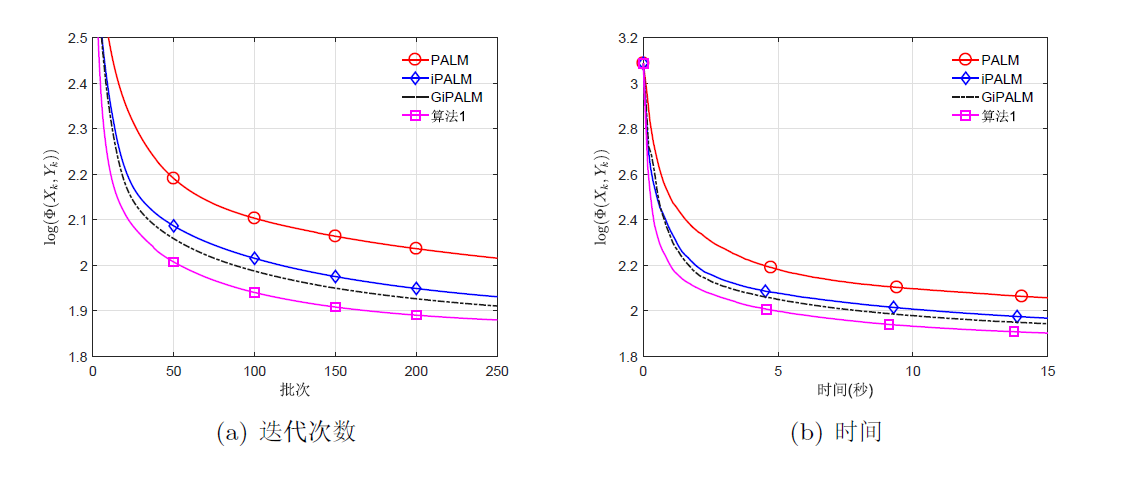
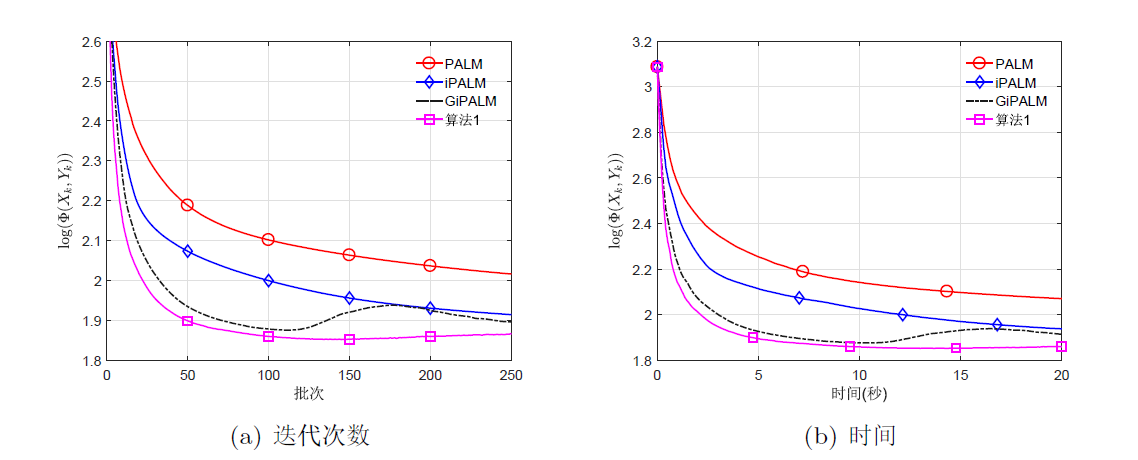
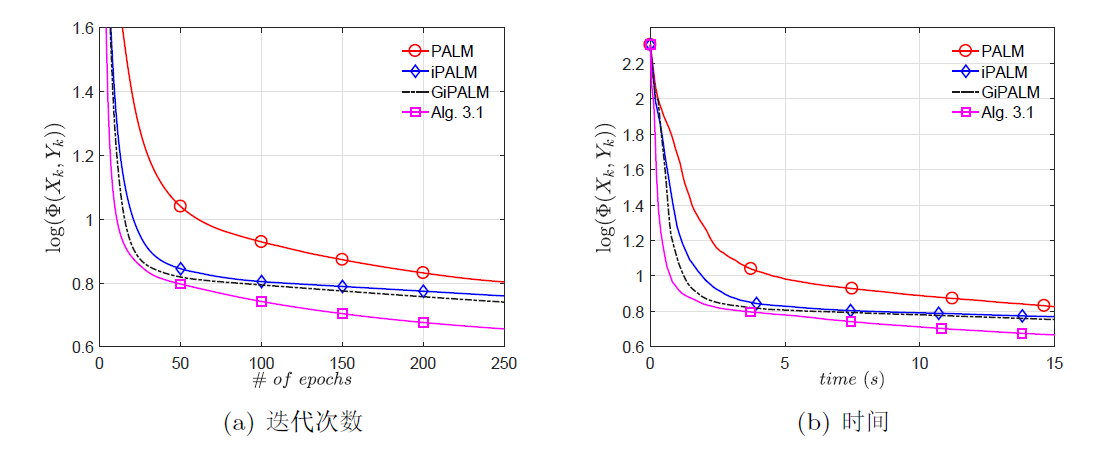
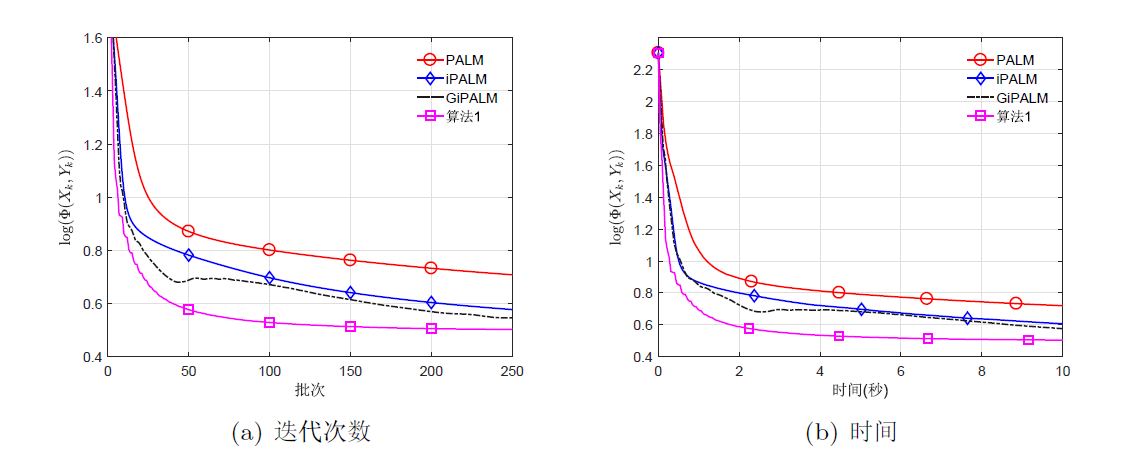
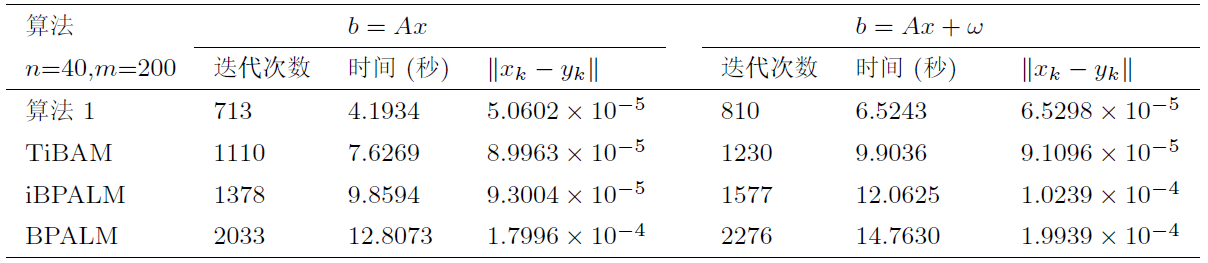
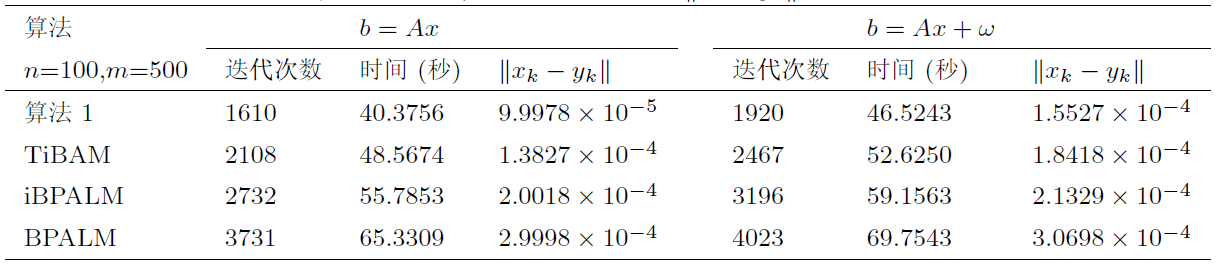
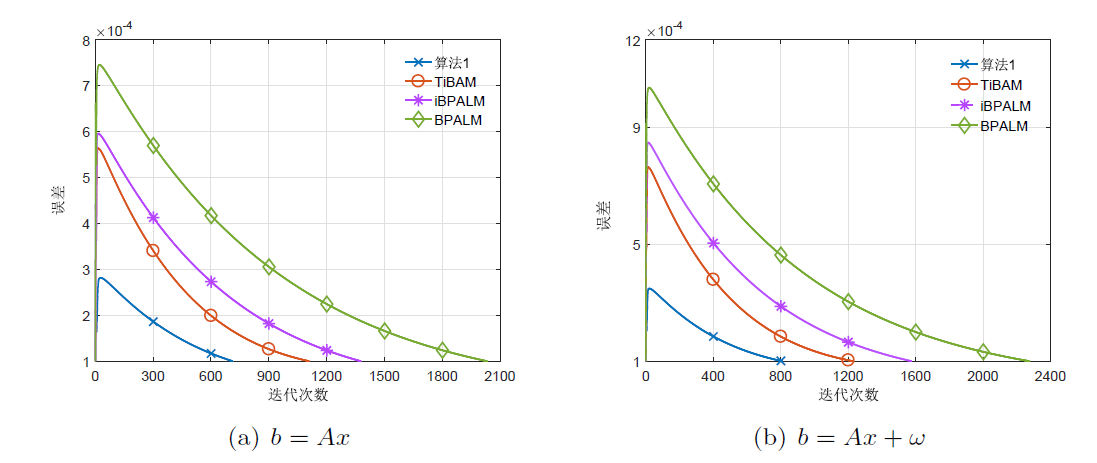
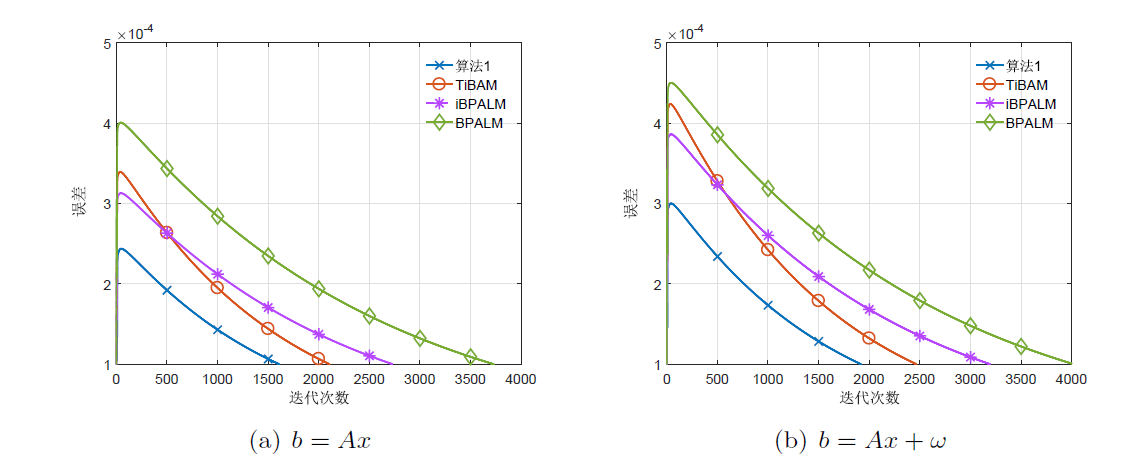
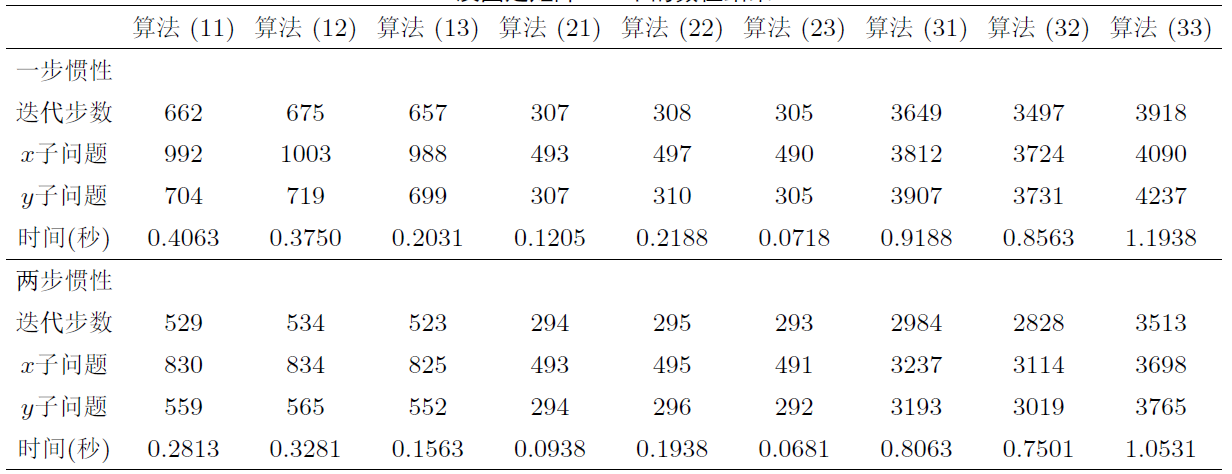
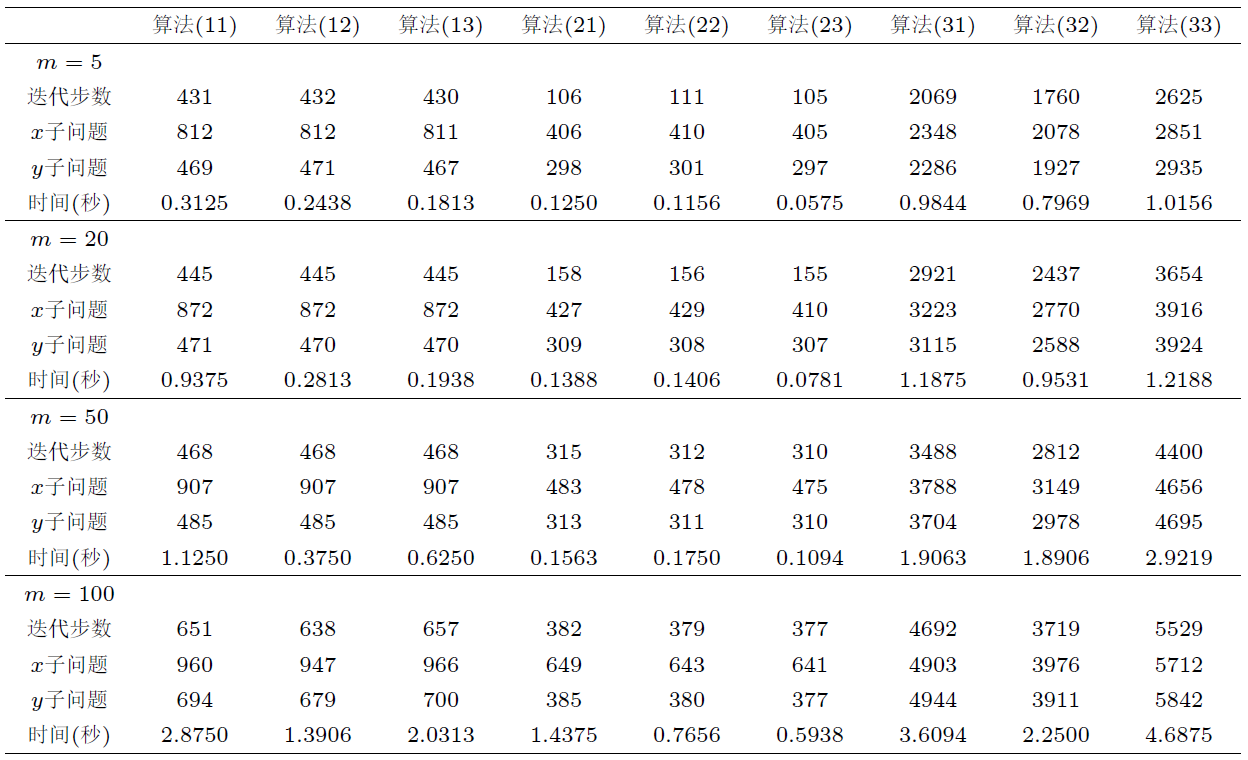
针对一类非凸非光滑不可分优化问题, 该文基于邻近交替线性极小化算法, 结合两步惯性外推和 Bregman 距离提出了一种新的迭代算法. 通过构造适当的效益函数, 利用 Kurdyka-Łojasiewicz 性质, 证明了所提出算法生成的迭代序列具有收敛性. 最后, 将该算法应用于稀疏非负矩阵分解、信号恢复、二次分式规划问题, 通过数值算例表明了提出算法的有效性.

关键词: 非凸非光滑优化, 邻近交替线性极小化, 惯性外推, Bregman 距离, Kurdyka-Łojasiewicz 性质

Abstract:

In this paper, for solving a class of nonconvex and nonsmooth nonseparable optimization problems, based on proximal alternating linearized minimization method we propose a new iterative algorithm which combines two-step inertial extrapolation and Bregman distance. By constructing appropriate benefit function, with the help of Kurdyka-Łojasiewicz property we establish the convergence of the whole sequence generated by proposed algorithm. We apply the proposed algorithm to solve sparse nonnegative matrix factorization, signal recovery and quadratic fractional programming problems, and show the effectiveness of proposed algorithm.

Key words: Nonconvex and nonsmooth optimization, Proximal alternating linearized minimization, Inertial extrapolation, Bregman distance, Kurdyka-Łojasiewicz property

中图分类号:

O224

赵静, 郭晨正. 非凸非光滑优化问题的两步惯性 Bregman 邻近交替线性极小化算法[J]. 数学物理学报, 2024, 44(6): 1630-1651.

Jing Zhao, Chenzheng Guo. Two-Step Inertial Bregman Proximal Alternating Linearized Minimization Algorithm for Nonconvex and Nonsmooth Problems[J]. Acta mathematica scientia,Series A, 2024, 44(6): 1630-1651.

图/表 12

图1

图2

图3

图4

图5

图6

表1

表2

图7

图8

表3

表4

参考文献 40

[1]	简金宝, 林惠, 马国栋. 大规模非凸不可分优化问题的分裂序列二次规划算法. 数学物理学报, 2023, 43A(4): 1284-1296
	Jian J b, Lin H, Ma G D. A Splitting sequence quadratic programming algorithm for the Large-Scale nonconvex nonseparable optimization problems. Acta Math sci, 2023, 43A(4): 1284-1296
[2]	刘富勤, 彭建文, 罗洪林. 具有线性化技术的三块非凸不可分优化问题 Bregman ADMM 收敛性分析. 数学物理学报, 2023, 43A(1): 291-304
	Liu F Q, Peng J W, Luo H L. Convergence analysis of Bregman ADMM for three-block nonconvex indivisible optimization problems with linearization technique. Acta Math Sci, 2023, 43A(1): 291-304
[3]	陈建华, 彭建文. 非凸多块优化的 Bregman ADMM 的收敛率研究. 数学物理学报, 2024, 44A(1): 195-208
	Chen J H, Peng J W. Research on the convergence rate of Bregman ADMM for nonconvex multiblock optimization. Acta Math Sci, 2024, 44A(1): 195-208
[4]	Nikolova M, Ng M K, Zhang S Q, Ching W K. Efficient reconstruction of piecewise constant images using nonsmooth nonconvex minimization. SIAM J Imaging Sci, 2008, 1(1): 2-25
[5]	Gu S H, Zhang L, Zuo W M, Feng X C. Weighted nuclear norm minimization with application to image denoising. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2014: 2862-2869
[6]	Bian W, Chen X J. Linearly constrained non-Lipschitz optimization for image restoration. SIAM J Imaging Sci, 2015, 8(4): 2294-2322
[7]	Bolte J, Sabach S, Teboulle M. Proximal alternating linearized minimization for nonconvex and nonsmooth problems. Math Program, 2014, 146(1): 459-494
[8]	Bot R I, Csetnek E R, Vuong P T. The forward-backward-forward method from continuous and discrete perspective for pseudo-monotone variational inequalities in Hilbert spaces. Eur J Oper Res, 2020, 287(1): 49-60
[9]	Attouch H, Bolte J, Svaiter B F. Convergence of descent methods for semi-algebraic and tame problems: proximal algorithms, forward-backward splitting, and regularized Guass-Seidel methods. Math Program, 2013, 137(1): 91-129
[10]	Donoho D L. Compressed sensing. IEEE Trans Inform Theory, 2006, 52(4): 1289-1306
[11]	Boyd S, Parikh N, Chu E, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers. Foundations and Trends in Machine Learning, 2011, 3(1): 1-122
[12]	Bertsekas D P, Tsitsiklis J N. Parallel and Distributed Computation: Numerical Methods. Englewood Cliffs, NJ: Prentice Hall, 1989
[13]	Bertsekas D P. Nonlinear programming. J Oper Res Soc, 1977, 48(3): 334-334
[14]	Beck A, Tetruashvili L. On the convergence of block coordinate descent type methods. SIAM J Optim, 2013, 23(4): 2037-2060
[15]	Auslender A. Asymptotic properties of the Fenchel dual functional and applications to decomposition problems. J Optim Theory Appl, 1992, 73(3): 427-449
[16]	Attouch H, Bolte J, Redont P, Soubeyran A. Proximal alternating minimization and projection methods for nonconvex problems: an approach based on the Kurdyka-Łojasiewicz inequality. Math Oper Res, 2010, 35(2): 438-457
[17]	Nikolova M, Tan P. Alternating structure-adapted proximal gradient descent for nonconvex block-regularised problems. SIAM J Optim, 2019, 29(3): 2053-2078
[18]	Ochs P, Chen Y, Brox T, Pock T. iPiano: Inertial proximal algorithm for nonconvex optimization. SIAM J Imaging Sci, 2014, 7(2): 1388-1419
[19]	Bot R I, Csetnek E R. An inertial Tseng's type proximal algorithm for nonsmooth and nonconvex optimization problems. J Optim Theory Appl, 2016, 171(2): 600-616
[20]	Polyak B T. Some methods of speeding up the convergence of iteration methods. USSR Comput Math Math Phys, 1964, 4(5): 1-17
[21]	Le T K H, Nicolas G, Panagiotis P. Inertial block proximal methods for non-convex non-smooth optimization. Proceedings of the 37th International Conference on Machine Learning, PMLR, 2020, 119: 5671-5681
[22]	Feng J K, Zhang H B, Zhang K L, Zhao P F. An inertial Douglas-Rachford splitting algorithm for nonconvex and nonsmooth problems. Concurrency and Computation Practice and Experience, 2023, 35(17): e6343
[23]	Zhang Y X, He S N. Inertial proximal alternating minimization for nonconvex and nonsmooth problems. J Inequal Appl, 2017, 2017: 1-13
[24]	Pock T, Sabach S. Inertial proximal alternating linearized minimization (iPALM) for nonconvex and nonsmooth problems. SIAM J Imaging Sci, 2017, 9(4): 1756-1787
[25]	Gao X, Cai X J, Han D R. A Gauss-Seidel type inertial proximal alternating linearized minimization for a class of nonconvex optimization problems. J Glob Optim, 2020, 76: 863-887
[26]	Wang Q X, Han D R. A generalized inertial proximal alternating linearized minimization method for nonconvex nonsmooth problems. Appl Numer Math, 2023, 189: 66-87
[27]	Yang X, Xu L L. Some accelerated alternating proximal gradient algorithms for a class of nonconvex nonsmooth problems. J Glob Optim, 2023, 87(2): 939-964
[28]	Zhao J, Dong Q L, Michael Th R, Wang F H. Two-step inertial Bregman alternating minimization algorithm for nonconvex and nonsmooth problems. J Glob Optim, 2022, 84(4): 941-966
[29]	Chao M T, Nong F F, Zhao M Y. An inertial alternating minimization with Bregman distance for a class of nonconvex and nonsmooth problems. J Appl Math Comput, 2023, 69(2): 1559-1581
[30]	Mordukhovich B. Variational Analysis and Generalized Differentiation. I: Basic Theory. Berlin: Springer-Verlag, 2006
[31]	Bolte J, Daniilidis A, Lewis A. The Łojasiewicz inequality for nonsmooth subanalytic functions with applications to subgradient dynamical systems. SIAM J Optim, 2006, 17(4): 1205-1223
[32]	Rockafellar R T, Wets R. Variational Analysis. Berlin: Springer, 1998
[33]	Wang F H, Cao W F, Xu Z B. Convergence of multi-block Bregman ADMM for nonconvex composite problems. Sci China Inf Sci, 2018, 61: 122101
[34]	Xu Y, Yin W. A block coordinate descent method for regularized multiconvex optimization with applications to nonnegative tensor factorization and completion. SIAM J Imaging Sci, 2013, 6(3): 1758-1789
[35]	Hsieh Y P, Kao Y C, Mahabadi R K, et al. A non-Euclidean gradient descent framework for nonconvex matrix factorization. IEEE Trans Signal Process, 2018, 66(22): 5917-5926
[36]	Lee D D, Seung H S. Learning the parts of objects by non-negative matrix factorization. Nature, 1999, 401(6755): 788-791
[37]	Pan J, Gillis N. Generalized separable nonnegative matrix factorization. IEEE Trans Pattern Anal Mach Intell, 2021, 43(5): 1546-1561
[38]	Rousset F, Peyrin F, Ducros N. A semi nonnegative matrix factorization technique for pattern generalization in single-pixel imaging. IEEE Trans Comput Imaging, 2018, 4(2): 284-294
[39]	Peharz R, Pernkopf F. Sparse nonnegative matrix factorization with $l_0$-constraints. Neurocomputing, 2012, 80: 38-46 pmid: 22505792
[40]	Xu Z B, Chang X Y, Xu F M, Zhang H. $L_{1/2}$ regularization: a thresholding representation theory and a fast solver. IEEE Trans Neural Netw Learning Syst, 2012, 23(7): 1013-1027