VALUE DISTRIBUTION PROPERTIES FOR GAUSS MAPS OF IMMERSED HARMONIC SURFACES RAMIFIED OVER HYPERSURFACES

Abstract

References

Metrics

doi:10.1007/s10473-024-0616-y

Abstract: In this paper, we study the value distribution properties of the generalized Gauss maps of weakly complete harmonic surfaces immersed in $\mathbb{R}^{m}$ , which is the case where the generalized Gauss map $\Phi$ is ramified over a family of hypersurfaces $\{Q_{j}\}_{j=1}^{q}$ in $\mathbb{P}^{m-1}(\mathbb{C})$ located in the $N$ -subgeneral position. In addition, we investigate the Gauss curvature estimate for the $K$ -quasiconformal harmonic surfaces immersed in $\mathbb{R}^{3}$ whose Gauss maps are ramified over a family of hypersurfaces located in the $N$ -subgeneral position.

Key words: immersed harmonic surface, generalized Gauss map, hypersurface, ramification, quasiconformal mapping, Gauss curvature

CLC Number:

32H25

Canhui LU, Xingdi CHEN. VALUE DISTRIBUTION PROPERTIES FOR GAUSS MAPS OF IMMERSED HARMONIC SURFACES RAMIFIED OVER HYPERSURFACES[J].Acta mathematica scientia,Series B, 2024, 44(6): 2341-2360.

Trendmd

[1] Ahlfors L V.An extension of Schwarz's lemma. Trans Amer Math Soc, 1938, 43: 359-364
[2] Aladro G, Krantz S G.A criterion for normality in

C^{m}

$\mathbb{C}^{m}$ . J Math Anal Appl, 1991, 161: 1-8
[3] Alarcón A, López F J.On harmonic quasiconformal immersions of surfaces in

R^{3}

$\mathbb{R}^{3}$ . Trans Amer Math Soc, 2013, 365(4): 1711-1742
[4] An D P, Quang S D, Thai D D.The second main theorem for meromorphic mappings into a complex projective space. Acta Math Vietnam, 2013, 38(1): 187-205
[5] Campana F, Winkelmann J.A Brody theorem for orbifolds. Manuscripta Math, 2009, 128(2): 195-212
[6] Chen X D, Li Y Z, Liu Z X, Ru M.Curvature estimate on an open Riemann surface with induced metric. Math Z, 2021, 298(1/2): 451-467
[7] Chen X D, Liu Z X, Ru M.Value distribution properties for the Gauss maps of the immersed harmonic surfaces. Pacific J Math, 2020, 309(2): 267-287
[8] Fujimoto H.Modified defect relations for the Gauss map of minimal surfaces. II. J Differential Geom, 1990, 31(2): 365-385
[9] Fujimoto H. On the number of exceptional values of the Gauss maps of minimal surfaces. J Math Soc Japan, 1988,

40

$\mathbf{ 40}$ (2): 235-247
[10] Fujimoto H.Value Distribution Theory the Gauss Map of Minimal Surfaces in

R^{m}

$\mathbb{R}^{m}$ . Braunschweig: Vieweg Teubner Verlag, 1993
[11] Ha P H.An estimate for the Gaussian curvature of minimal surfaces in

R^{m}

$\mathbb{R}^{m}$ whose Gauss map is ramified over a set of hyperplanes. Differential Geom Appl, 2014, 32: 130-138
[12] Jensen G R, Rigoli M.Harmonically immersed surfaces of

R^{n}

$\mathbb{R}^{n}$ . Trans Amer Math Soc, 1988, 307(1): 363-372
[13] Kalaj D.The Gauss map of a hamonic surface. Indag Math (NS), 2013, 24(3): 415-427
[14] Kalaj D, Vujadinović D.Quasiconformal harmonic graphs. Complex Var Elliptic Equ, 2023, 68(8): 1407-1418
[15] Klotz T.Surfaces harmonically immersed in

E^{3}

$E^{3}$ . Pacific J Math, 1967, 21(1): 79-87
[16] Klotz T.A complete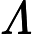

R_{Λ}

$R_{\varLambda}$ -harmonically immersed surface in

E^{3}

$E^{3}$ on which

H \neq 0

$H\not=0$ . Proc Amer Math Soc, 1968, 19: 1296-1298
[17] Liu X J, Pang X C.Normal family theory and Gauss curvature estimate of minimal surfaces in

R^{m}

$\mathbb{R}^{m}$ . J Differential Geom, 2016, 103(2): 297-318
[18] Liu Z X, Li Y Z, Chen X D. The value distribution of Gauss maps of immersed harmonic surfaces with ramification. Acta Math Sci, 2022,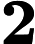

42 B

$\mathbf{42B}$ (1): 172-186
[19] Lu C H, Chen X D.Unicity theorem for generalized Gauss maps of immersed harmonic surfaces. J Math Anal Appl, 2023, 519: 126827
[20] Milnor T K.Are harmonically immersed surfaces at all like minimally immersed surfaces?// Seminar on Minimal Submanifolds. Princeton: Princeton University Press, 1983: 99-110
[21] Milnor T K.Harmonically immersed surfaces. J Differential Geom, 1979, 14(2): 205-214
[22] Milnor T K.Restrictions on the curvatures of

Ψ

$\Psi$ -bounded surfaces. J Differential Geom, 1976, 11(1): 31-46
[23] Osserman R, Ru M.An estimate for the Gauss curvature of minimal surfaces in

R^{m}

$\mathbb{R}^{m}$ whose Gauss map omits a set of hyperplanes. J Differential Geom, 1997, 46: 578-593
[24] Quang S D.Curvature estimate and the ramification of the holomorphic maps over hypersurfaces on Riemann surfaces. Bull Soc Math France, 2023, 151(1): 91-115
[25] Quang S D.Modified defect relation of Gauss maps on annular ends of minimal surfaces for hypersurfaces of projective varieties in subgeneral position. J Math Anal Appl, 2024, 23(1): 127806
[26] Quang S D.Modified defect relation of Gauss maps of minimal surfaces for hypersurfaces of projective varieties in subgeneral position. arXiv:2107.08986
[27] Ru M.Gauss map of minimal surfaces with ramification. Trans Amer Math Soc, 1993, 339(2): 751-764
[28] Ru M.Nevanlinna Theory and Its Relation to Diophantine Approximation. Hackensack, NJ: World Scientific Publishing, 2021
[29] Ru M.On the Gauss map of minimal surfaces immersed in

R^{n}

$\mathbb{R}^{n}$ . J Differential Geom, 1991, 34(2): 411-423

Just accepted

Online first

Just accepted

Online first

Viewed

Full text

	From	local

	Times	2
	Rate	100%

Abstract

Just accepted	Online first	Issue

0	0	27

	From	Others

	Times	27
	Rate	100%

Cited

Web of Science	Crossref	ScienceDirect	Search for Citations in Google Scholar >>


This page requires you have already subscribed to WoS.

Shared

Discussed