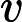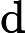[1] Arumugam G, Tyagi J.Keller-Segel chemotaxis models: A review. Acta Appl Math, 2021, 171: Art 6
[2] Bellomo N, Bellouquid A, Tao Y, Winkler M. Toward a mathematical theory of Keller-Segel models of pattern formation on biological tissues. Math Models Methods Appl Sci, 2015, 25: 1663-1763
[3] Burger M, Laurencot P, Trescases A. Delayed blow-up for chemotaxis models with local sensing. J Lond Math Soc, 2021, 103: 1596-1617
[4] Chu J, Jin H, Xiong L. Global dynamics of a tumor invasion model with/without logistic source. Z Angew Math Phys, 2021, 72: Art 181
[5] Fujie K. Global asymptotic stability in a chemotaxis-growth model for tumor invasion. Discrete Contin Dyn Syst Ser S, 2020, 13: 203-209
[6] Fujie K, Ishida S, Ito A, Yokota T. Large time behavior in a chemotaxis model with nonlinear general diffusion for tumor invasion. Funkcial Ekvac, 2018, 61: 37-80
[7] Fujie K, Ito A, Winkler M, Yokota T. Stabilization in a chemotaxis model for tumor invasion. Discrete Contin Dyn Syst, 2016, 36: 151-169
[8] Fujie K, Ito A, Yokota T. Existence and uniqueness of local classical solutions to modified tumor invasion models of Chaplain-Anderson type. Adv Math Sci Appl, 2014, 24: 67-84
[9] Fujie K, Jiang J. Global existence for a kinetic model of pattern formation with density-suppressed motilities. J Differential Equations, 2020, 269: 5338-5378
[10] Fujie K, Jiang J. Boundedness of classical solutions to a degenerate Keller-Segel type model with signal-dependent motilities. Acta Appl Math, 2021, 176: Art 3
[11] Fujie K, Jiang J. Comparison methods for a Keller-Segel-type model of pattern formations with density-suppressed motilities. Calc Var Partial Differential Equations, 2021, 60: Art 92
[12] From1970 until present: the Keller-Segel model in chemotaxis and its consequences I. Jahresber Deutsch Math-Verein, 2003, 105: 103-165
[13] Ito A. A mass-conserved tumor invasion systemwith quasi-variational degenerate diffusion. Anal Appl, 2022, 20: 615-680
[14] Jin H, Kim Y, Wang Z. Boundedness, stabilization,pattern formation driven by density-suppressed motility. SIAM J Math, 2018, 78: 1632-1657
[15] Jin H, Liu Z, Shi S. Global dynamics of a quasilinear chemotaxis model arising from tumor invasion. Nonlinear Anal: Real World Appl, 2018, 44: 18-39
[16] Jin H, Wang Z. Critical mass on the Keller-Segel system with signal-dependent motility. Proc Amer Math Soc, 2020, 148: 4855-4873
[17] Jin H, Wang Z. The Keller-Segel system with logistic growth and signal-dependent motility. Discrete Contin Dyn Syst Ser B, 2021, 26: 3023-3041
[18] Jin H, Xiang T. Boundedness and exponential convergence in a chemotaxis model for tumor invasion. Nonlinearity, 2016, 29: 3579-3596
[19] Keller E, Segel L. Model for chemotaxis. J Theor Biol, 1971, 30: 225-234
[20] Li D, Wu C. Effects of density-suppressed motility in a two-dimensional chemotaxis model arising from tumor invasion. Z Angew Math Phys, 2020, 71: Art 153
[21] Liu C, Fu X, Liu L, et al. Sequential establishment of stripe patterns in an expanding cell population. Science, 2011, 334: 238-241
[22] Liu Z, Xu J. Large time behavior of solutions for density-suppressed motility system in higher dimensions. J Math Anal Appl, 2019, 475: 1596-1613
[23] Lv W, Wang Q. Global existence for a class of Keller-Segel models with signal-dependent motility and general logistic term. Evol Equ Control Theory, 2021, 10: 25-36
[24] Lv W, Wang Q. An  -dimensional chemotaxis system with signal-dependent motility and generalized logistic source: global existence and asymptotic stabilization. Proc Roy Soc Edinburgh Sect A, 2021, 151: 821-841 -dimensional chemotaxis system with signal-dependent motility and generalized logistic source: global existence and asymptotic stabilization. Proc Roy Soc Edinburgh Sect A, 2021, 151: 821-841
[25] Lyu W, Wang Z. Logistic damping effect in chemotaxis models with density-suppressed motility. Adv Nonlinear Anal, 2022, 12: 336-355
[26] Mizoguchi N, Souplet P. Nondegeneracy of blow-up points for the parabolic Keller-Segel system. Ann Inst H Poincaré Anal Non Liné$aire, 2014, 31: 851-875
[27] Osawa R, Yokota T. Boundedness in a chemotaxis model with nonlinear diffusion and logistic type source for tumor invasion. Adv Math Sci Appl, 2018, 27: 225-240
[28] Tao X, Fang Z. Global boundedness and stability in a density-suppressed motility model with generalized logistic source and nonlinear signal production. Z Angew Math Phys, 2022, 73: Art 123
[29] Tao Y, Winkler M. Effects of signal-dependent motilities in a Keller-Segel-type reaction-diffusion system. Math Models Methods Appl Sci, 2017, 27: 1645-1683
[30] Teller J. On a comparison method for a parabolic-elliptic system of chemotaxis with density-suppressed motility and logistic growth. Rev Real Acad Cienc Exactas Fis Nat Ser A-Mat, 2022, 116: Art 109
[31] Tu X, Mu C, Qiu S, Zhang J. Boundedness and asymptotic stability in a chemotaxis model with signal-dependent motility and nonlinear signal secretion. Commun Math Anal Appl, 2022, 1: 568-589
[32] Wang J, Wang M. Boundedness in the higher-dimensional Keller-Segel model with signal-dependent motility and logistic growth. J Math Phys, 2019, 60: 011507
[33] Winkler M. Aggregation vs. global diffusive behavior in the higher-dimensional Keller-Segel model. J Differential Equation, 2010, 248: 2889-2905
[34] Yoon C, Kim Y. Global existence and aggregation in a Keller-Segel model with Fokker-Planck diffusion. Acta Appl Math, 2017, 149: 101-123 |