数学物理学报(英文版) ›› 2023, Vol. 43 ›› Issue (1): 303-323.doi: 10.1007/s10473-023-0117-4
EXISTENCE OF A GROUND STATE SOLUTION FOR THE CHOQUARD EQUATION WITH NONPERIODIC POTENTIALS*
Yuanyuan Luo, Dongmei Gao, Jun Wang†
- Institute of Applied System Analysis, Jiangsu University, Zhenjiang 212013, China
-
收稿日期:2021-05-18修回日期:2022-06-11发布日期:2023-03-01 -
通讯作者:†Jun WANG.E-mail: wangmath2011@126.com -
基金资助:*National Natural Science Foundation of China (11971202), and Outstanding Young foundation of Jiangsu Province (BK20200042).
EXISTENCE OF A GROUND STATE SOLUTION FOR THE CHOQUARD EQUATION WITH NONPERIODIC POTENTIALS*
Yuanyuan Luo, Dongmei Gao, Jun Wang†
- Institute of Applied System Analysis, Jiangsu University, Zhenjiang 212013, China
-
Received:2021-05-18Revised:2022-06-11Published:2023-03-01 -
Contact:†Jun WANG.E-mail: wangmath2011@126.com -
About author:Yuanyuan Luo,E-mail:lyy201901@126.com; Dongmei Gao,E-mail:mei3221652898@126.com -
Supported by:*National Natural Science Foundation of China (11971202), and Outstanding Young foundation of Jiangsu Province (BK20200042).
摘要: We study the Choquard equation 













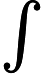

















































































引用本文
Yuanyuan Luo, Dongmei Gao, Jun Wang. EXISTENCE OF A GROUND STATE SOLUTION FOR THE CHOQUARD EQUATION WITH NONPERIODIC POTENTIALS*[J]. 数学物理学报(英文版), 2023, 43(1): 303-323.
Yuanyuan Luo, Dongmei Gao, Jun Wang. EXISTENCE OF A GROUND STATE SOLUTION FOR THE CHOQUARD EQUATION WITH NONPERIODIC POTENTIALS*[J]. Acta mathematica scientia,Series B, 2023, 43(1): 303-323.
使用本文
| [1] Lieb E H.Existence and uniqueness of the minimizing solution of Choquard’s nonlinear equation. Studies in Appl Math, 1977, 57(2): 93-105 [2] Pekar S I.Untersuchungüber die Elektronentheorie der Kristalle. Akademie-Verlag, 1954 [3] Jones K R W. Newtonian quantum gravity. Austral J Phys, 1995, 48(6): 1055-1082 [4] Moroz I M, Penrose R, Tod P.Spherically-symmetric solutions of the Schrödinger-Newton equations. Classical & Quantum Gravity, 1998, 15(9): 2733-2742 [5] Lions P L.The Choquard equation and related questions. Nonlinear Anal, 1980, 4(6): 1063-1072 [6] Lions P L.The concentration-compactness principle in the calculus of variations. The locally compact case, part 1. Ann Inst H Poincaré Anal Non Linéaire, 1984, 1(2): 109-145 [7] Lions P L.The concentration-compactness principle in the calculus of variations. The locally compact case, part 2. Ann Inst H Poincaré Anal Non Linéaire, 1984, 1(4): 223-283 [8] Ackermann N.On a periodic Schrödinger equation with nonlocal superlinear part. Math Z, 2004, 248(2): 423-443 [9] Wei J, Winter M.Strongly interacting bumps for the Schrödinger-Newton equations. J Math Phys, 2009, 50(1): 012905 [10] Ma L, Zhao L.Classification of positive solitary solutions of the nonlinear Choquard equation. Arch Ration Mech Anal, 2010, 195(2): 455-467 [11] Moroz V, Van Schaftingen J.Ground states of nonlinear Choquard equations: existence, qualitative properties and decay asymptotics. J Funct Anal, 2013, 265(2): 153-184 [12] Moroz V, Van Schaftingen J.Existence of ground states for a class of nonlinear Choquard equations. Trans Amer Math Soc, 2015, 367(9): 6557-6579 [13] Moroz V, Van Schaftingen J.Nonexistence and optimal decay of supersolutions to Choquard equations in exterior domains. J Differ Equ, 2013, 254(8): 3089-3145 [14] Moroz V, Van Schaftingen J.A guide to the Choquard equation. J Fixed Point Theory Appl, 2017, 19(1): 773-813 [15] Moroz V, Van Schaftingen J.Ground states of nonlinear Choquard equations: Hardy-Littlewood-Sobolev critical exponent. Comm Contemp Math, 2015, 17(05): 1550005 [16] Cao D.The existence of nontrivial solutions to a generalized Choquard-Pekar equation. Acta Math Sci, 1989, 9(1): 101-112 (in Chinese) [17] Buffoni B, Jeanjean L, Stuart C A.Existence of a nontrivial solution to a strongly indefinite semilinear equation. Proc Amer Math Soc, 1993, 119(1): 179-186 [18] Alves C O, Nóbrega A B, Yang M B.Multi-bump solutions for Choquard equation with deepening potential well. Calc Var Partial Differential Equations, 2016, 55(3): 1-28; Proc Amer Math Soc, 1993, 119(1): 179-186 [19] Lenzmann E.Uniqueness of ground states for pseudorelativistic Hartree equations. Analysis & PDE, 2009, 2(1): 1-27 [20] Ghimenti M, Van Schaftingen J.Nodal solutions for the Choquard equation. J Funct Anal, 2016, 271(1): 107-135 [21] Cingolani S, Clapp M, Secchi S.Multiple solutions to a magnetic nonlinear Choquard equation. Z Angew Math Phys, 2012, 63(2): 233-248 [22] Clapp M, Salazar D.Positive and sign changing solutions to a nonlinear Choquard equation. J Math Anal Appl, 2013, 407(1): 1-15 [23] Cingolani S, Secchi S.Ground states for the pseudo-relativistic Hartree equation with external potential. Proc Roy Soc Edinburgh Sect A, 2015, 145(1): 73-90 [24] Cingolani S, Clapp M, Secchi S.Intertwining semiclassical solutions to a Schröinger-Newton system. Discrete Contin Dyn Syst Ser S, 2013, 6(4): 891-908 [25] Cingolani S, Secchi S, Squassina M.Semi-classical limit for Schrödinger equations with magnetic field and Hartree-type nonlinearities. Proc Roy Soc Edinburgh Sect A, 2010, 140(5): 973-1009 [26] Moroz V, Van Schaftingen J.Semi-classical states for the Choquard equation. Calc Var Partial Differential Equations, 2015, 52(1): 199-235 [27] Cingolani S, Secchi S.Semiclassical analysis for pseudo-relativistic Hartree equations. J Differ Equ, 2015, 258(12): 4156-4179 [28] Dohnal T, Plum M, Reichel W.Surface gap soliton ground states for the nonlinear Schrödinger equation. Comm Math Phys, 2011, 308(2): 511-542 [29] Lieb E H, Loss M.Analysis. volume 14 of Graduate Studies in Math. Providence, RI: Amer Math Soc, 2001 [30] Wang J, Tian L X, Xu J X, et al.Existence of multiple positive solutions for Schrödinger-Poisson systems with critical growth. Z Angew Math Phys, 2015, 66(5): 2441-2471 [31] Ruiz D.The Schrödinger-Poisson equation under the effect of a nonlinear local term. J Funct Anal, 2006, 237(2): 655-674 [32] Struwe M.Variational methods. Applications to Nonlinear Partial Differential Equations and Hamiltonian Systems. Fourth edition. Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics [Results in Mathematics and Related Areas. 3rd Series. A Series of Modern Surveys in Mathematics]. Berlin: Springer-Verlag, 2008 [33] Pankov A.Periodic nonlinear Schrödinger equation with application to photonic crystals. Milan J Math, 2005, 73(1): 259-287 [34] Liu Z L, Su J B, Wang Z Q.Solutions of elliptic problems with nonlinearities of linear growth. Calc Var Partial Differential Equations, 2009, 35(4): 463-480 [35] Zhu M C, Wang J, Qian X Y.Existence of solutions to nonlinear Schrödinger equations involving NLaplacian and potentials vanishing at infinity. Acta Math Sin Engl Ser, 2020, 36(10): 1151-1170 [36] Jiang Y S, Zhou H S.Bound states for a stationary nonlinear Schrödinger-Poisson system with sign-changing potential in R3. Acta Math Sci, 2009, 29B(4): 1095-1104 |
| Viewed | ||||||||||||||||||||||||||||||||||||||||||||||
|
Full text 7
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Abstract 106
|
|
|||||||||||||||||||||||||||||||||||||||||||||
Cited |
|
|||||||||||||||||||||||||||||||||||||||||||||
| Shared | ||||||||||||||||||||||||||||||||||||||||||||||
| Discussed | ||||||||||||||||||||||||||||||||||||||||||||||
