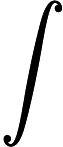数学物理学报(英文版) ›› 2022, Vol. 42 ›› Issue (3): 1003-1017.doi: 10.1007/s10473-022-0311-9
SINGULAR CONTROL OF STOCHASTIC VOLTERRA INTEGRAL EQUATIONS
Nacira AGRAM1, Saloua LABED2, Bernt ØKSENDAL3, Samia YAKHLEF2
- 1. Department of Mathematics, KTH Royal Institute of Technology, 10044, Stockholm, Sweden;
2. University Mohamed Khider of Biskra, Biskra, Algeria;
3. Department of Mathematics, University of Oslo, PO Box 1053 Blindern, N-0316, Oslo, Norway
SINGULAR CONTROL OF STOCHASTIC VOLTERRA INTEGRAL EQUATIONS
Nacira AGRAM1, Saloua LABED2, Bernt ØKSENDAL3, Samia YAKHLEF2
- 1. Department of Mathematics, KTH Royal Institute of Technology, 10044, Stockholm, Sweden;
2. University Mohamed Khider of Biskra, Biskra, Algeria;
3. Department of Mathematics, University of Oslo, PO Box 1053 Blindern, N-0316, Oslo, Norway
摘要: This paper deals with optimal combined singular and regular controls for stochastic Volterra integral equations, where the solution is given by
Here denotes the Brownian motion Itô type
differential, denotes the singular control (singular in time
with respect to Lebesgue measure) and denotes the regular
control (absolutely continuous with respect to Lebesgue measure).
Such systems may for example be used to model harvesting of populations with memory, where represents the population density at time , and the singular control process represents the harvesting effort rate. The total income from the harvesting is represented by
for the given functions and , where is a
constant denoting the terminal time of the harvesting. Note that it
is important to allow the controls to be singular, because in some
cases the optimal controls are of this type.
Using Hida-Malliavin calculus, we prove sufficient conditions and necessary conditions of optimality of controls. As a consequence, we obtain a new type of backward stochastic Volterra integral equations with singular drift.
Finally, to illustrate our results, we apply them to discuss optimal harvesting problems with possibly density dependent prices.
中图分类号:
- 60H05