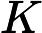关键词: Laplace transforms, Fourier transform, tubular domain, regular cone

Abstract: Assume that $ 0< p<\infty $ and that $B$ is a connected nonempty open set in $\mathbb{R}^n$, and that $A^{p}(B)$ is the vector space of all holomorphic functions $F$ in the tubular domains $\mathbb{R}^n+{\rm i}B$ such that for any compact set $ K \subset B,$ $$ \|y\mapsto \|x\mapsto F(x+{\rm i}y)\|_{L^p(\mathbb{R}^n)}\|_{L(K)}<\infty, $$ so $A^p(B)$ is a Fréchet space with the Heine-Borel property, its topology is induced by a complete invariant metric, is not locally bounded, and hence is not normal. Furthermore, if $1\leq p\leq 2$, then the element $F$ of $A^{p}(B)$ can be written as a Laplace transform of some function $f\in L(\mathbb{R}^n)$.

Key words: Laplace transforms, Fourier transform, tubular domain, regular cone