数学物理学报(英文版) ›› 2019, Vol. 39 ›› Issue (2): 413-419.doi: 10.1007/s10473-019-0207-5
A FOUR-WEIGHT WEAK TYPE MAXIMAL INEQUALITY FOR MARTINGALES
任颜波
- School of Mathematics and Statistics, Henan University of Science and Technology, Luoyang 471003, China
A FOUR-WEIGHT WEAK TYPE MAXIMAL INEQUALITY FOR MARTINGALES
Yanbo REN
- School of Mathematics and Statistics, Henan University of Science and Technology, Luoyang 471003, China
摘要: In this article, some necessary and sufficient conditions are shown in order that weighted inequality of the form
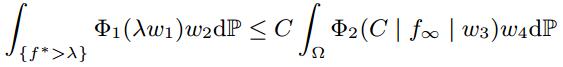
holds a.e. for uniformly integrable martingales f = (fn)n≥0 with some constant C > 0, where Φ1, Φ2 are Young functions, wi (i = 1, 2, 3, 4) are weights, ![]() and f∞ =
and f∞ = ![]() fn a.e. As an application, two-weight weak type maximal inequalities of martingales are considered, and particularly a new equivalence condition is presented.
fn a.e. As an application, two-weight weak type maximal inequalities of martingales are considered, and particularly a new equivalence condition is presented.