| [1] |
Iragi B C, Munyakazi J B. A uniformly convergent numerical method for a singularly perturbed Volterra integro-differential equation. Int J Comput Math, 2020, 97(4): 759-771
|
| [2] |
Hoppensteadt F C. An algorithm for approximate solutions to weakly filtered synchronous control systems and nonlinear renewal processes. SIAM J Appl Math, 1983, 43(4): 834-843
|
| [3] |
Lodge A S, McLeod J B, Nohel J A. A nonlinear singularly perturbed Volterra integrodifferential equation occurring in polymer rheology. Proc R Soc Edinburgh Sect A, 1978, 80(1/2): 99-137
|
| [4] |
Jordan G S. A nonlinear singularly perturbed Volterra integrodifferential equation of nonconvolution type. Proc R Soc Edinburgh Sect A, 1978, 80(3/4): 235-247
|
| [5] |
Yapman Ö, Amiraliyev G M. A novel second-order fitted computational method for a singularly perturbed Volterra integro-differential equation. Int J Comput Math, 2020, 97(6): 1293-1302
|
| [6] |
Şevgin S. Numerical solution of a singularly perturbed Volterra integro-differential equation. Adv Difference Equ, 2014, 171: 1-15
|
| [7] |
Huang J, Cen Z, Xu A, Liu L B. A posteriori error estimation for a singularly perturbed Volterra integro-differential equation. Numer Algorithms, 2020, 83(2): 549-563
|
| [8] |
Sumit S, Kumar J, Vigo-Aguiar. Analysis of a nonlinear singularly perturbed Volterra integro-differential equation. J Comput Appl Math, 2021, Article 113410
|
| [9] |
Nhan T A, Vulanović R. Analysis of the truncation error and barrier-function technique for a Bakhvalov-type mesh. Electron Trans Numer Anal, 2019, 51: 315-330
|
| [10] |
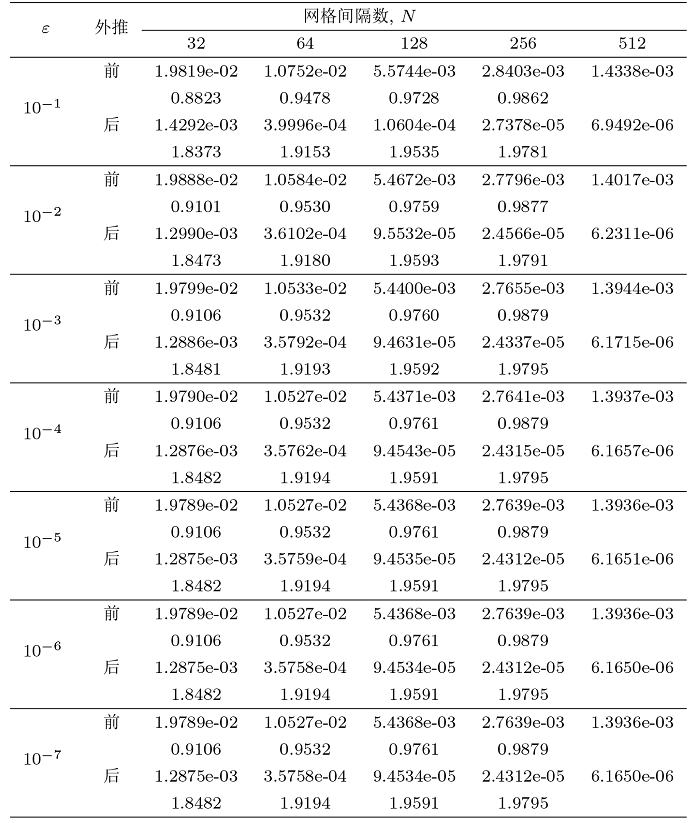
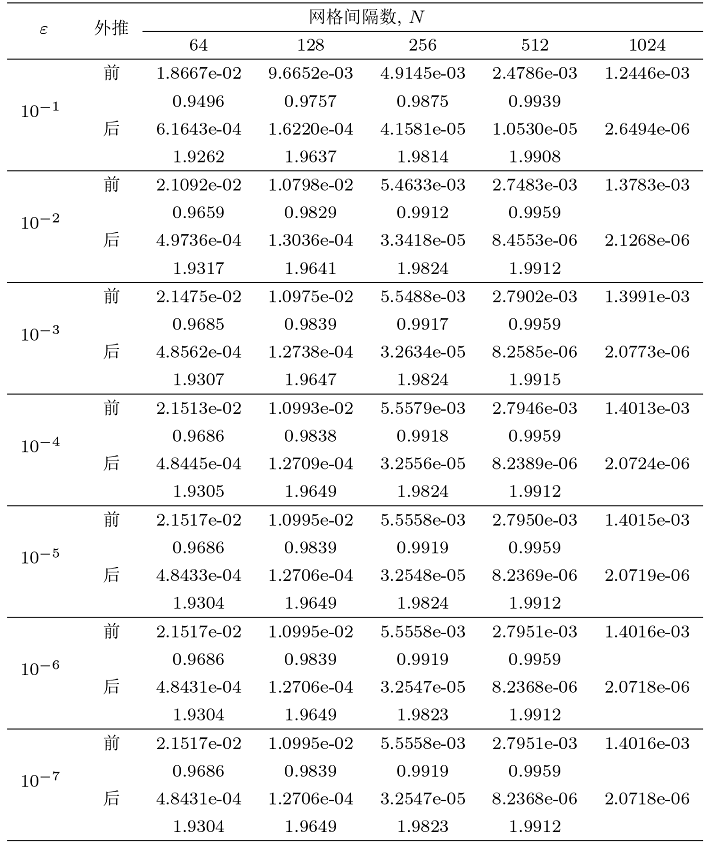
Long G, Liu L B, Huang Z. Richardson extrapolation method on an adaptive grid for singularly perturbed Volterra integro-differential equations. Numer Funct Anal Optim, 2021, 42: 739-757
|
| [11] |
Linß T. Error expansion for a first-order upwind difference scheme applied to a model convection-diffusion problem. IMA J Numer Anal, 2004, 24: 239-253
|
| [12] |
Bakhvalov N S. The optimization of methods of solving boundary value problems with a boundary layer. Comp Math Math Phys, 1969, 9(4): 139-166
|
| [13] |
Boglaev I P. Approximate solution of a nonlinear boundary value problem with a small parameter at the highest-order derivative. USSR Comput Math Math Phys, 1984, 24(6): 30-35
|
| [14] |
Andreev V B, Kopteva N V. On the convergence, uniform with respect to a small parameter of monotone three-point finite difference approximations. Differ Equations, 1998, 34(7): 921-929
|
| [15] |
Kopteva N V. On the uniform with respect to a small parameter convergence of the central difference scheme on condensing meshes. Comp Math Math Phys, 1999, 39(10): 1594-1610
|
| [16] |
Kopteva N. Uniform pointwise convergence of difference schemes for convection-diffusion problems on layer-adapted meshes. Computing, 2001, 66: 179-197
|
| [17] |
Vulanović R. On a numerical solution of a type of singularly perturbed boundary value problem by using a special discretization mesh. Univ u Novom Sadu Zb Rad Prir Mat Fak Ser Mat, 1983, 13: 187-201
|
| [18] |
Linß T. Sufficient conditions for uniform convergence on layer-adapted grids. Appl Numer Math, 2001, 37: 241-255
|
| [19] |
Roos H G, Linß T. Sufficient conditions for uniform convergence on layer-adapted grids. Computing, 1999, 63: 27-45
|
| [20] |
Kudu M, Amirali I, Amiraliyev G M. A finite-difference method for a singularly perturbed delay integro-differential equation. J Comput Appl Math, 2016, 308: 379-390
|
| [21] |
Amiraliyev G M, Şevgin S. Uniform difference method for singularly perturbed Volterra integro-differential equations. Applied Mathematics and Computation, 2006, 179(2): 731-741
|
 ),Liao Yige(
),Liao Yige( ),Long Guangqing(
),Long Guangqing( )
)