Acta mathematica scientia,Series A ›› 2024, Vol. 44 ›› Issue (4): 978-993.
Previous Articles Next Articles
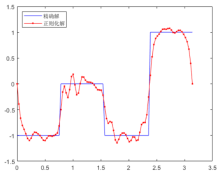
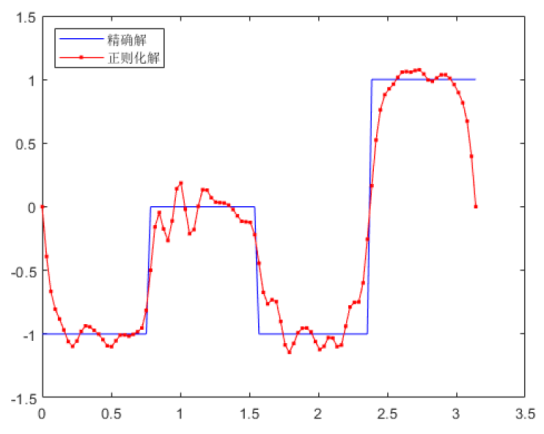
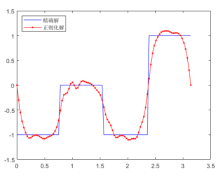
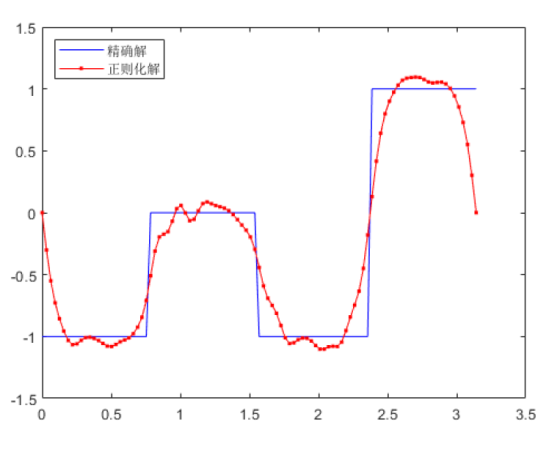
Fractional Tikhonov Regularization Method for an Inverse Boundary Value Problem of the Fractional Elliptic Equation
- School of Mathematics and Information Science, North Minzu University, Yinchuan 750021
-
Received:2023-05-05Revised:2024-01-10Online:2024-08-26Published:2024-07-26 -
Supported by:NSF of Ningxia(2022AAC03234);NSF of China(11761004);Construction Project of First-Class Disciplines in Ningxia Higher Education(NXYLXK2017B09)
CLC Number:
- O175
Cite this article
Zhang Xiao, Zhang Hongwu. Fractional Tikhonov Regularization Method for an Inverse Boundary Value Problem of the Fractional Elliptic Equation[J].Acta mathematica scientia,Series A, 2024, 44(4): 978-993.
share this article
| [1] | Algazin O D. Exact solution to the Dirichlet problem for degenerating on the boundary elliptic equation of Tricomi-Keldysh type in the half-space. 2016, arXiv:1603.05760 |
| [2] | Neto J B, Gelfand I M. Fundamental solutions for the Tricomi operator. Duke Math J, 1999, 98(3): 465-483 |
| [3] | Neto J B, Gelfand I M. Fundamental solutions for the Tricomi operator, II. Duke Math J, 2002, 111(3): 561-584 |
| [4] | Neto J B, Gelfand I M. Fundamental solutions of the Tricomi operator, III. Duke Math J, 2005, 128(1): 119-140 |
| [5] | Moiseev E I. On the solution of a nonlocal boundary value problem by the spectral method. Differ Equ, 1999, 35(8): 1094-1100 |
| [6] |
Xu N, Yin H. The weighted     |
| [7] | Bers L. Mathematical Aspects of Subsonic and Transonic Gas Dynamics. New York: Wiley, 1958 |
| [8] | Otway T H. The Dirichlet Problem for Elliptic-Hyperbolic Equations of Keldysh Type. Berlin: Springer, 2012 |
| [9] | Nakhushev A. On mathematical and information technologies for modeling and control of regional development. Dokl Adygsk (Cherkessk) Mezhdunar Akad Nauk, 2007, 9(1): 128-137 |
| [10] | Brndle C, Colorado E, de Pablo A. A concave-convex elliptic problem involving the fractional Laplacian. Proc Roy Soc Edinburgh Sect A, 2013, 143(1): 39-71 |
| [11] | Ambrosio V, Freddi L, Musina R. Asymptotic analysis of the Dirichlet fractional Laplacian in domains becoming unbounded. J Math Anal Appl, 2020, 485(2): 123845 |
| [12] | Caffarelli L, Silvestre L. An extension problem related to the fractional Laplacian. Comm Partial Differential Equations, 2007, 32(8): 1245-1260 |
| [13] | Masaeva O K. Dirichlet problem for the generalized Laplace equation with the Caputo derivative. Differ Equ, 2012, 48(3): 449-454 |
| [14] | Kirane M, Turmetov B K, Torebek B T. A nonlocal fractional Helmholtz equation. Fract Differ Calc, 2017, 7(2): 225-234 |
| [15] | Podlubny I. Fractional Differential Equations. San Diego: Academic Press, 1999 |
| [16] | Ruzhansky M, Torebek B T, Turmetov B. Well-posedness of Tricomi-Gellerstedt-Keldysh-type fractional elliptic problems. J Integral Equations Appl, 2022, 34(3): 373-387 |
| [17] | Cimmino G. Sulle equazioni lineari alle derivate parziali del secondo ordine di tipo ellittico sopra una superficie chiusa. Atti Accad Naz Lincei Rend Lincei Mat Appl, 1938, 7(1): 73-96 |
| [18] | Gellerstedt S. Sur un probleme aux limites pour une equation linearire aux derivees partielles du second ordre de type mixtes. Uppsala: Uppsala University, 1935 |
| [19] | Keldysh M. On some cases of degenerate elliptic equations on the boundary of a domain. Dokl Akad Nauk, 1951, 77: 181-183 |
| [20] | Roumaissa S, Nadjib B, Faouzia R, et al. Iterative regularization method for an abstract ill-posed generalized elliptic equation. Asian-Eur J Math, 2021, 14(5): 2150069 |
| [21] | Xiong X, Xue X. A fractional Tikhonov regularization method for identifying a space-dependent source in the time-fractional diffusion equation. Appl Math Comput, 2019, 349: 292-303 |
| [22] | Tran N, Au V V, Zhou Y, et al. On a final value problem for fractional reaction-diffusion equation with Riemann-Liouville fractional derivative. Math Methods Appl Sci, 2020, 43(6): 3086-3098 |
| [23] | Zheng G H, Zhang Q G. Solving the backward problem for space-fractional diffusion equation by a fractional Tikhonov regularization method. Math Comput Simulation, 2018, 148: 37-47 |
| [24] | Djennadi S, Shawagfeh N, Arqub O A. A fractional Tikhonov regularization method for an inverse backward and source problems in the time-space fractional diffusion equations. Chaos Solitons Fractals, 2021, 150: 111127 |
| [25] | Kilbas A A, Saigo M. On solution of integral equation of Abel-Volterra type. Differential Integral Equations, 1995, 8(5): 993-1011 |
| [26] | Boudabsa L, Simon T, Vallois P. Fractional extreme distributions. Electron J Probab, 2020, 25: 1-20 |
| [27] | Bianchi D, Buccini A, Donatelli M, et al. Iterated fractional Tikhonov regularization. Inverse Problems, 2015, 31(5): 055005 |
| [28] | Morozov V A, Nashed Z, Aries A B. Methods for Solving Incorrectly Posed Problems. New York: Springer, 1984 |
| [1] | Hongwu Zhang. One Regularization Method for a Cauchy Problem of Semilinear Elliptic Equation [J]. Acta mathematica scientia,Series A, 2022, 42(1): 45-57. |
| [2] | Xiaomin Yang,Zhipeng Qiu,Ling Ding. Complex Dynamics of an Intraguild Predation Model [J]. Acta mathematica scientia,Series A, 2019, 39(4): 963-970. |
| [3] | Han Huan, Li Xing, Liu Jun, Ni Chengzhou. Two-Dimensional Differential Model and Numerical Method of Undersea Cables During Installation [J]. Acta mathematica scientia,Series A, 2015, 35(4): 780-793. |
| Viewed | ||||||||||||||||||||||||||||||||||||||||||||||
|
Full text 58
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Abstract 62
|
|
|||||||||||||||||||||||||||||||||||||||||||||
Cited |
|
|||||||||||||||||||||||||||||||||||||||||||||
| Shared | ||||||||||||||||||||||||||||||||||||||||||||||
| Discussed | ||||||||||||||||||||||||||||||||||||||||||||||
|