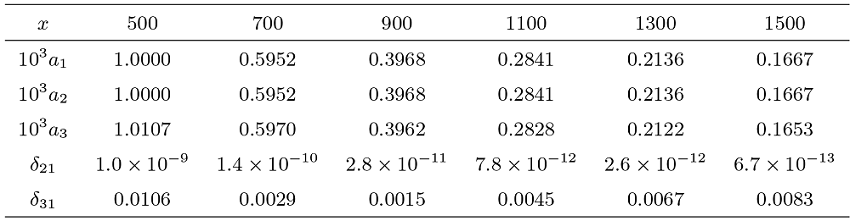
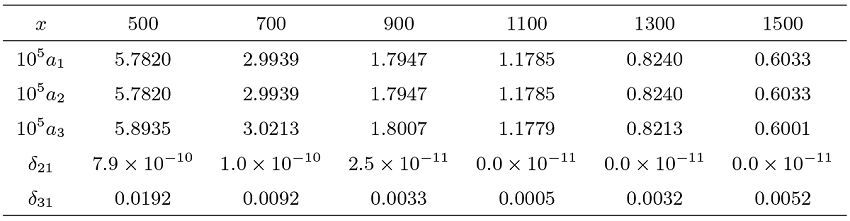
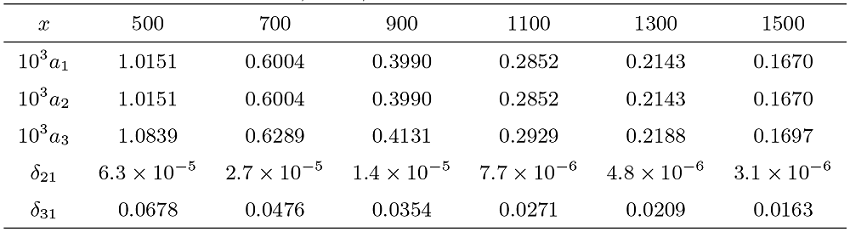
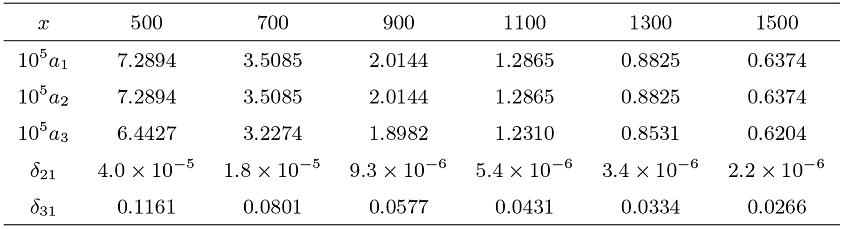
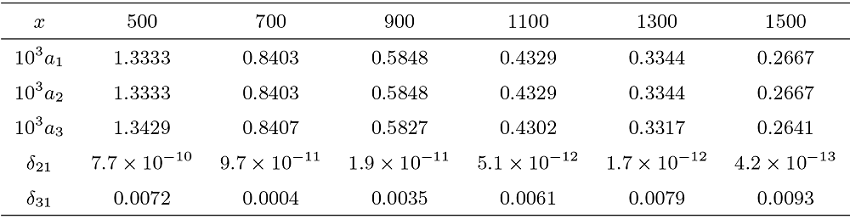
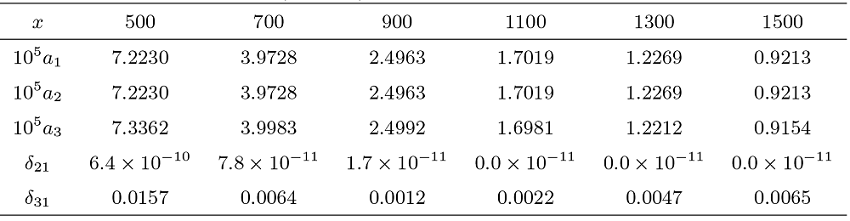
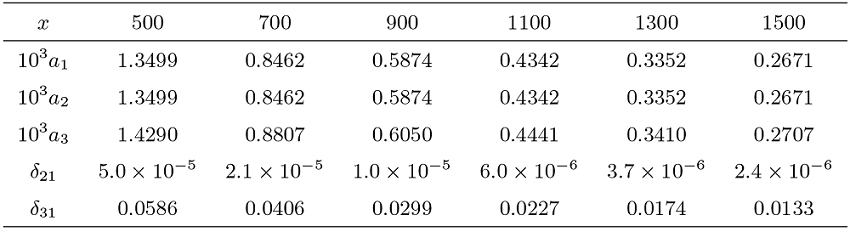
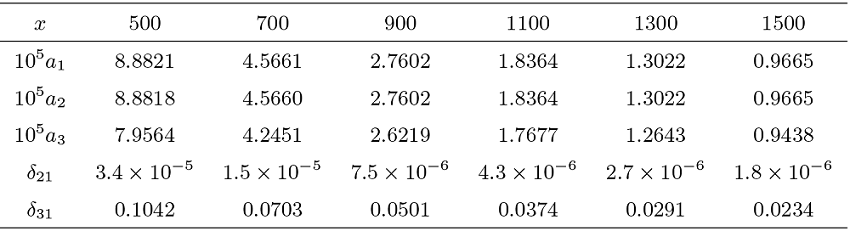
Acta mathematica scientia,Series A ›› 2024, Vol. 44 ›› Issue (4): 1110-1125.
Local Max-sum Equivalence of Random Variables with Bernstein Copula
Ming Ruixing1( ),Lou Zhenhan1(
),Lou Zhenhan1( ),Cui Sheng2,3,*(
),Cui Sheng2,3,*( ),Gong Chan2,3(
),Gong Chan2,3( )
)
- 1School of Statistics and Mathematics, Zhejiang Gongshang University, Hangzhou 310018
2Science College,China Three Gorges University, Hubei Yichang 443002
3Three Gorges Mathematical Research Center,China Three Gorges University, Hubei Yichang 443002
-
Received:2023-12-01Revised:2024-04-29Online:2024-08-26Published:2024-07-26 -
Supported by:Characteristic & Preponderant Discipline of Key Construction Universities in Zhejiang Province (Zhejiang Gongshang University–Statistics), the Collaborative Innovation Center of Statistical Data Engineering Technology & Application, Digital + Discipline Construction Project(SZJ2022B004);Research on Minimum Variance Portfolio of Zhejiang Statistical Science Research Base Project in High dimension(22TJD02);Scientific Research and Application Project of Universities in Yichang City(A21-3-018)
CLC Number:
- O175.23
Cite this article
Ming Ruixing, Lou Zhenhan, Cui Sheng, Gong Chan. Local Max-sum Equivalence of Random Variables with Bernstein Copula[J].Acta mathematica scientia,Series A, 2024, 44(4): 1110-1125.
share this article
| [1] | Embrechts P, Goldie C M. On closure and factorization properties of subexponential and related distributions. J Aust Math Soc Ser A, 1980, 29(2): 243-256 |
| [2] | Geluk J L, De Vries C G. Weighted sums of subexponential random variables and asymptotic dependence between returns on reinsurance equities. Insurance Math Econom, 2006, 38(1): 39-56 |
| [3] | Wang D, Tang Q. Maxima of sums and random sums for negatively associated random variables with heavy tails. Stat Probabil Lett, 2004, 68(3): 287-295 |
| [4] | Albrecher H, Asmussen S, Kortschak D, et al. Tail asymptotics for the sum of two heavy-tailed dependent risks. Extremes, 2006, 9(2): 107-130 |
| [5] | Geluk J, Ng K W. Tail behavior of negatively associated heavy-tailed sums. J Appl Probab, 2006, 43(2): 587-593 |
| [6] | Wang K, Wang Y. Notes on the asymptotics of the tail probabilities of sums for negatively associated random variables with heavy tails. Chinese J Appl Probab Stat, 2007, 23(4): 337-344 |
| [7] | Chen Y, Yuen K C. Sums of pairwise quasi-asymptotically independent random variables with consistent variation. Stoch Models, 2009, 25(1): 76-89 |
| [8] | Geluk J, Tang Q. Asymptotic tail probabilities of sums of dependent subexponential random variables. J Theor Probab, 2009, 22: 871-882 |
| [9] | Foss S, Richards A. On sums of conditionally independent subexponential random variables. Math Oper Res, 2010, 35(1): 102-119 |
| [10] | Yang Y, Wang K, Leipus R, et al. Tail behavior of sums and maxima of sums of dependent subexponential random variables. Acta Appl Math, 2011, 114(3): 219-231 |
| [11] | Chen W, Yu C, Wang Y. Some discussions on the local distribution classes. Stat Probabil Lett, 2013, 83(7): 1654-1661 |
| [12] | Li J. On pairwise quasi-asymptotically independent random variables and their applications. Stat Probabil Lett, 2013, 83(9): 2081-2087 |
| [13] | Foss S, Korshunov D, Zachary S. An Introduction to Heavy-Tailed and Subexponential Distributions. New York: Springer, 2013 |
| [14] | Asmussen S, Foss S, Korshunov D. Asymptotics for sums of random variables with local subexponential behaviour. J Theor Probab, 2003, 16(2): 489-518 |
| [15] | Ng K, Tang Q. Asymptotic behavior of tail and local probabilities for sums of subexponential random variables. J Appl Probab, 2004, 41(1): 108-116 |
| [16] | Denisov D, Shneer V. Local asymptotics of the cycle maximum of a heavy-tailed random walk. Adv Appl Probab, 2007, 39(1): 221-244 |
| [17] | Denisov D, Dieker A B, Shneer V. Large deviations for random walks under subexponentiality: The big-jump domain. Ann Probab, 2008, 36(5): 1946-1991 |
| [18] | Cui Z, Wang Y, Wang K. Asymptotics for the moments of the overshoot and undershoot of a random walk. Adv Appl Probab, 2009, 41(2): 469-494 |
| [19] | Yang Y, Leipus R, Siaulys J. Local precise large deviations for sums of random variables with O-regularly varying densities. Stat Probabil Lett, 2010, 80(19/20): 1559-1567 |
| [20] |
刘希军, 王岳宝. 不同分布的卷积的局部封闭性及局部渐近性的充分条件和必要条件. 系统科学与数学, 2009, 29(4): 527-535
doi: 10.12341/jssms08391 |
|
Liu X J, Wang Y B. The sufficient condition and necessary condition of local closure and local asymptotic for the convolutions of non-identical distributions. J Syst Sci Math Sci, 2009, 29(4): 527-535
doi: 10.12341/jssms08391 |
|
| [21] | 江涛, 徐晖. Farlie-Gumbel-Morgenstern 联合分布的 Max-Sum 局部等价式. 中国科学: 数学, 2016, 46(1): 67-80 |
| Jiang T, Xu H. Max-Sum local equivalence of random variables with Farlie-Gumbel-Morgenstern joint distribution. Sci Sin Math, 2016, 46(1): 67-80 | |
| [22] | 柳福祥, 龚婵, 崔盛. 服从 FGM Copula 的实值重尾随机游动的局部 Max-Sum 等价. 江西师范大学学报 (自然科学版), 2020, 44(6): 609-613 |
| Liu F X, Gong C, Cui S. The local max-sum equivalence of real valued random walks with heavy-tailed increments following FGM copula. Journal of Jiangxi Normal University, 2020, 44(6): 609-613 | |
| [23] | Nelsen R B. An Introduction to Copulas. New York: Springer, 2006 |
| [24] | Sancetta A, Satchell S. The Bernstein copula and its applications to modeling and approximations of multivariate distributions. Economet Theor, 2004, 20(3): 535-562 |
| [25] | Bouezmarni T, Rombouts J V K, Taamouti A. Asymptotic properties of the Bernstein density copula estimator for α-mixing data. J Multivariate Anal, 2010, 101(1): 1-10 |
| [26] | Janssen P, Swanepoel J, Veraverbeke N. Large sample behavior of the Bernstein copula estimator. J Stat Plan Infer, 2012, 142(5): 1189-1197 |
| [27] | Swanepoel J W H, Allison J S. Some new results on the empirical copula estimator with applications. Stat Probabil Lett, 2013, 83(7): 1731-1739 |
| [28] | Tavin B. Application of Bernstein copulas to the pricing of multi-asset derivatives//Jaworski P, Durante F, Hardle W. Copulae in Mathematical and Quantitative Finance. Berlin: Springer, 2013: 277-288 |
| [29] | Hernández-Maldonado V, Díazviera M, Erdely A. A joint stochastic simulation method using the Bernstein copula as a flexible tool for modeling nonlinear dependence structures between petrophysical properties. J Petrol Sci Eng, 2012, 90-91: 112-123 |
| [30] | Hernández-Maldonado V, Díazviera M, Erdely A. A multivariate Bernstein copula model for permeability stochastic simulation. Geofis Int, 2014, 53(2): 163-181 |
| [31] | Diers D, Eling M, Marek S D. Dependence modeling in non-life insurance using the Bernstein copula. Insurance Math Econom, 2012, 50(3): 430-436 |
| [32] | 镇磊, 尹留志, 方兆本. 多项式 Copula 方法对市场相关结构的分析. 中国管理科学, 2008, 16(3): 1-7 |
| Zhen L, Yin L Z, Fang Z B. An analysis to dependence patterns in a polynomial copula approach. Chinese J Manag Sci, 2008, 16(3): 1-7 | |
| [33] | 龚婵. 相依重尾随机变量序列 Max-Sum 等价的相关研究. 宜昌: 三峡大学, 2021 |
| Gong C. Local Max-Sum equivalence of sequences of dependent heavy-tailed random variables. Yichang: China Three Gorges University, 2021 | |
| [34] | Coqueret G. Second order risk aggregation with the Bernstein copula. Insurance Math Econom, 2014, 58: 150-158 |
| [35] | 江涛, 明瑞星, 崔盛. 相依重尾风险模型的渐近分析. 北京: 科学出版社, 2019 |
| Jiang T, Ming R X, Cui S. Asymptotic Analysis of Dependent Risk Model with Heavy Tails. Beijing: Science Press, 2019 |
| [1] | Yu Ting, Dong Ying. The Convergence Rate of the Fast Signal Diffusion Limit for a Three-Dimensional Keller-Segel-Stokes System [J]. Acta mathematica scientia,Series A, 2024, 44(4): 925-945. |
| [2] | Xu Rui, Zhou Kaijuan, Bai Ning. A with-in Host HIV-1 Infection Dynamics Model Based on Virus-to-cell Infection and Cell-to-cell Transmission [J]. Acta mathematica scientia,Series A, 2024, 44(3): 771-782. |
| [3] | Liu Jinghua, Li Lin. Homeomorphic Solutions of Iterative Functional Equations [J]. Acta mathematica scientia,Series A, 2024, 44(2): 313-325. |
| [4] | Yang Zhaodi, He Kan, Duan Zhoubo. Entanglement Measure of Two-body Quantum System Based on the Wedge Product of Vectors [J]. Acta mathematica scientia,Series A, 2024, 44(1): 246-256. |
| [5] | Wu Peng, He Zerong. Spatio-temporal Dynamics of HIV Infection Model with Periodic Antiviral Therapy and Nonlocal Infection [J]. Acta mathematica scientia,Series A, 2024, 44(1): 209-226. |
| [6] | Jian Hui, Gong Min, Wang Li. On the Blow-Up Solutions of Inhomogeneous Nonlinear Schrödinger Equation with a Partial Confinement [J]. Acta mathematica scientia,Series A, 2023, 43(5): 1350-1372. |
| [7] | Li Yixian,Zhang Zhengjie. The Existence of Ground State Solutions for a Class of Equations Related to Klein-Gordon-Maxwell Systems [J]. Acta mathematica scientia,Series A, 2023, 43(3): 680-690. |
| [8] | Juan Wang,Jie Zhao. Homogenization of the Oscillating Robin Mixed Boundary Value Problems [J]. Acta mathematica scientia,Series A, 2021, 41(1): 81-90. |
| [9] | Juan Wang,Jie Zhao. Homogenization of Higher-Order Equations with Mixed Boundary Condition [J]. Acta mathematica scientia,Series A, 2020, 40(4): 925-933. |
| [10] | Yue Wang,Hongmin Suo,Wei Wei. Classical Solutions for a Kind of New Kirchhoff-Type Problems Without Boundary Constraint [J]. Acta mathematica scientia,Series A, 2020, 40(4): 857-868. |
| [11] | Wencui Liang,Zhengjie Zhang. Multiple Solutions for Nonlinear Equations Related to Kirchhoff Type Equations [J]. Acta mathematica scientia,Series A, 2020, 40(4): 842-849. |
| [12] | Juan Wang,Jie Zhao. Homogenization of the Neumann Boundary Value Problem: The Sharper W1, p Estimate [J]. Acta mathematica scientia,Series A, 2019, 39(5): 1115-1124. |
| [13] | Yingfei Fan, Guopeng Zhang, Xinguo Jiang, jian Ma. Attracting and Quasi-Invariant Sets of Second-Order Neutral Stochastic Partial Differential Equations [J]. Acta mathematica scientia,Series A, 2018, 38(6): 1135-1143. |
| [14] | Zhao Jihong. Logarithmical Regularity Criteria in Terms of Pressure for the Three Dimensional Dissipative System Modeling Electro-Hydrodynamics [J]. Acta mathematica scientia,Series A, 2018, 38(3): 549-564. |
| [15] | Tong Yuxia, Zheng Shenzhou, Cheng Linna. Removable Singularities of Weakly A-Harmonic Tensors [J]. Acta mathematica scientia,Series A, 2017, 37(6): 1001-1011. |
|