Acta mathematica scientia,Series A ›› 2023, Vol. 43 ›› Issue (5): 1471-1482.
Previous Articles Next Articles
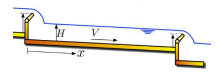
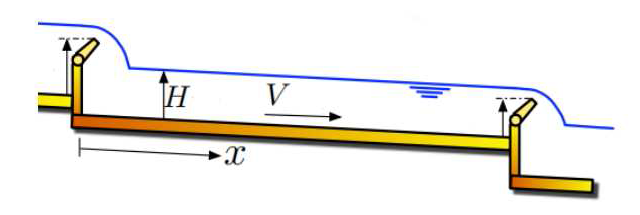
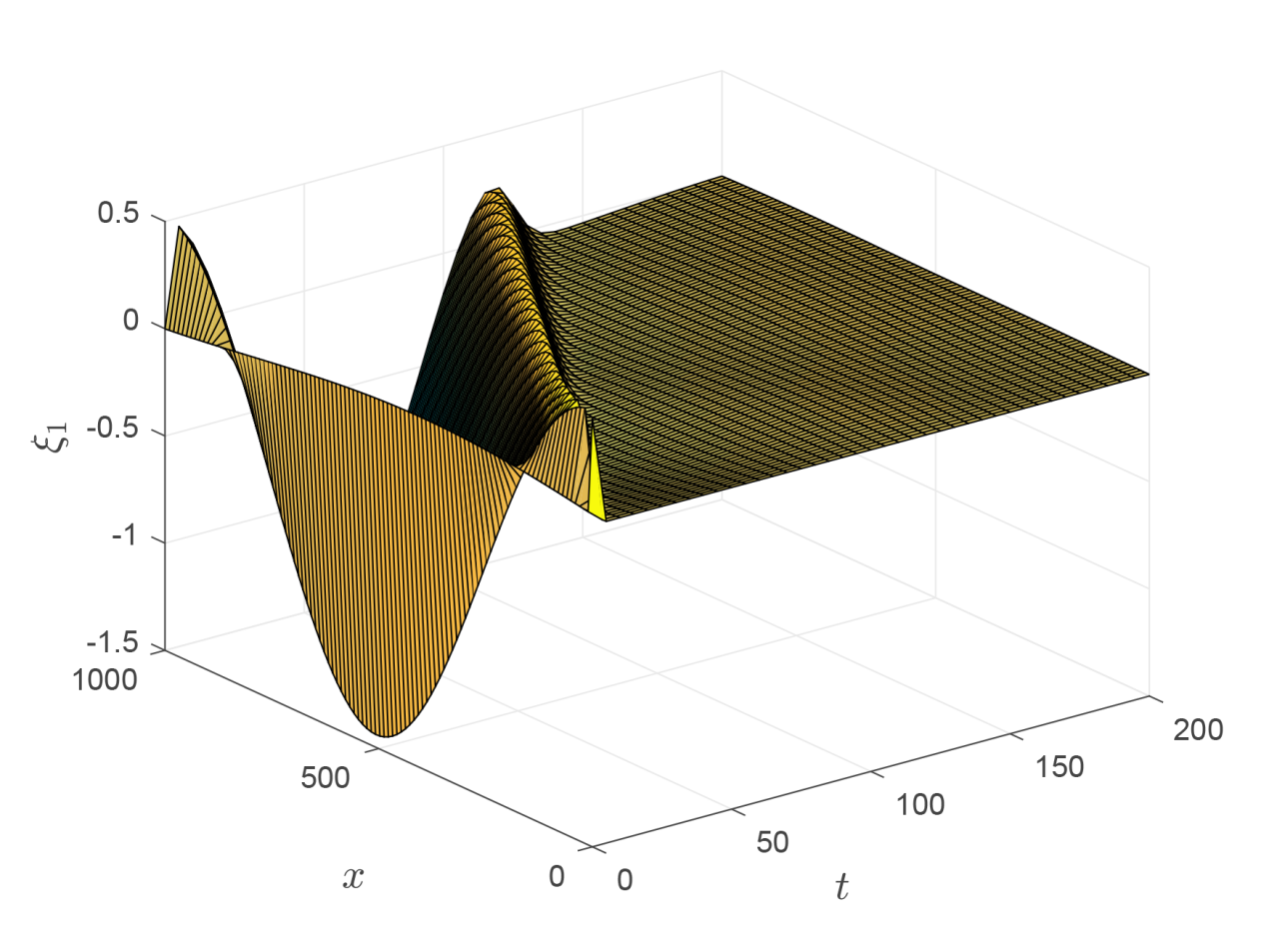
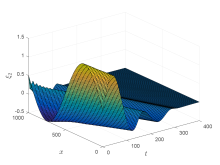
The PDP Boundary Control for a Class of 2× 2 Hyperbolic Partial Differential System
Pang Yuting1( ),Zhao Dongxia1,*(
),Zhao Dongxia1,*( ),Zhao Xin2(
),Zhao Xin2( ),Gao Caixia1(
),Gao Caixia1( )
)
- 1School of Mathematics, North University of China, Taiyuan 030051
2School of Electrical and Power Engineering, Taiyuan University of Technology, Taiyuan 030024
-
Received:2022-03-18Revised:2023-03-08Online:2023-10-26Published:2023-08-09 -
Contact:Dongxia Zhao E-mail:2116786325@qq.com;zhaodongxia6@sina.com;1808642517@qq.com;1519546532@qq.com -
Supported by:Fundamental Research Program of Shanxi Province(20210302123046)
CLC Number:
- O231.4
Cite this article
Pang Yuting,Zhao Dongxia,Zhao Xin,Gao Caixia. The PDP Boundary Control for a Class of 2
share this article
| [1] |
Litrico X, Fromion V, Baume J P, et al. Experimental validation of a methodology to control irrigation canals based on Saint-Venant equations. Control Engineering Practice, 2005, 13(11): 1425-1437
doi: 10.1016/j.conengprac.2004.12.010 |
| [2] |
Santos V D, Prieur C. Boundary control of open channels with numerical and experimental validations. IEEE Transactions on Control Systems Technology, 2008, 16(6): 1252-1264
doi: 10.1109/TCST.2008.919418 |
| [3] |
Bastin G, Coron J M, Tamasoiu S O. Stability of linear density-flow hyperbolic systems under PI boundary control. Automatica, 2015, 53: 37-42
doi: 10.1016/j.automatica.2014.12.025 |
| [4] |
Zhang L G, Prieur C, Qiao J F. PI boundary control of linear hyperbolic balance laws with stabilization of ARZ traffic flow models. Systems & Control Letters, 2019, 123: 85-91
doi: 10.1016/j.sysconle.2018.11.005 |
| [5] | Bastin G, Coron J M. Stability and Boundary Stabilization of 1-D Hyperbolic Systems. Switzerland: Birkhäuser, 2016 |
| [6] | Vazquez R, Krstic M, Coron J M. Backstepping boundary stabilization and state estimation of a 2×2 linear hyperbolic system. Orlando: IEEE Conference on Decision and Control and European Control Conference, 2011 |
| [7] |
Litrico X, Fromion V. Boundary control of hyperbolic conservation laws using a frequency domain approach. Automatica, 2009, 45(3): 647-656
doi: 10.1016/j.automatica.2008.09.022 |
| [8] | Bastin G, Coron J M, D'Andrea-Novel B, et al. Boundary control for exact cancellation of boundary disturbances in hyperbolic systems of conservation laws. Seville: IEEE Conference on Decision and Control, and the European Control Conference, 2005 |
| [9] |
Bastin G, Coron J M. Exponential stability of PI control for Saint-Venant equations with a friction term. Methods and Applications of Analysis, 2019, 26(2): 101-112
doi: 10.4310/MAA.2019.v26.n2.a1 |
| [10] |
Coron J M, D'Andrea-Novel B, Bastin G. A strict Lyapunov function for boundary control of hyperbolic systems of conservation laws. IEEE Transactions on Automatic Control, 2007, 52(1): 2-11
doi: 10.1109/TAC.2006.887903 |
| [11] | Pazy A. Semigroup of Linear Operators and Applications to Partial Differential Equations. New York: Springer-Verlag, 1983 |
| [12] |
Hayat A, Shang P P. A quadratic Lyapunov function for Saint-Venant equations with arbitrary friction and space-varying slope. Automatica, 2019, 100: 52-60
doi: 10.1016/j.automatica.2018.10.035 |
| [13] | Coron J M, Tamasoiu S O. Feedback stabilization for a scalar conservation law with PID boundary control. Chinese Annals of Mathematics, 2015, 36B(5): 763-776 |
| [14] |
Chentouf B, Wang J M. Boundary feedback stabilization and Riesz basis property of a 1-d first order hyperbolic linear system with L∞-coefficients. Journal of Differential Equations, 2009, 246(3): 1119-1138
doi: 10.1016/j.jde.2008.08.010 |
| [15] | Trinh N T, Andrieu V, Xu C Z. Boundary PI controllers for a star-shaped network of 2×2 systems governed by hyperbolic partial differential equations. International Federation of Automatic Control, 2017, 50(1): 7070-7075 |
| [16] |
Trinh N T, Andrieu V, Xu C Z. Output regulation for a cascaded network of 2×2 hyperbolic systems with PI controller. Automatica, 2018, 91: 270-278
doi: 10.1016/j.automatica.2018.01.010 |
| [17] | Aström K J, Hägglund T. PID Controllers: Theory, Design, and Tunning. Research Triangle Park, NC: ISA-The Instrumentation, Systems and Automation Society, 1995 |
| [18] |
Litrico X, Fromion V, Scorletti G. Robust feedforward boundary control of hyperbolic conservation laws. Networks and Heterogeneous Media, 2017, 2(4): 717-731
doi: 10.3934/nhm.2007.2.717 |
| [19] |
Bastin G, Coron J M, Hayat A. Feedforward boundary control of 2×2 nonlinear hyperbolic systems with application to Saint-Venant equations. European Journal of Control, 2021, 57: 41-53
doi: 10.1016/j.ejcon.2020.11.002 |
| [20] |
Tallman G, Smith O. Analog study of dead-beat posicast control. Ire Transactions on Automatic Control, 2003, 4(1): 14-21
doi: 10.1109/TAC.1958.1104844 |
| [21] | Silva G J, Datta A, Bhattacharyya S P. PID Controllers for Time-Delay Systems. Boston: Birkhäuser, 2005 |
| [22] | Cai G, Chen L. Some problems of delayed feedback control. Advances in Mechanics, 2013, 43(1): 21-28 |
| [23] |
Suh I H, Bien Z. Proportional minus delay controller. IEEE Transactions on Automatic Control, 1979, 24(2): 370-372
doi: 10.1109/TAC.1979.1102024 |
| [24] |
Suh I H, Bien Z. Use of time-delay actions in the controller design. IEEE Transactions on Automatic Control, 1980, 25: 600-603
doi: 10.1109/TAC.1980.1102347 |
| [25] | Atay F M. Balancing the inverted pendulum using position feedback. Applied Mathematics Letters, 1999, 12(5): 51-56 |
| [26] |
Hu H Y. Using delayed state feedback to stabilize periodic motions of an oscillator. Journal of Sound and Vibration, 2004, 275(3-5): 1009-1025
doi: 10.1016/j.jsv.2003.07.006 |
| [27] |
Liu B, Hu H. Stabilization of linear undamped systems via position and delayed position feedbacks. Journal of Sound and Vibration, 2008, 312(3): 509-525
doi: 10.1016/j.jsv.2007.11.001 |
| [28] |
Krstic M. Control of an unstable reaction-diffusion PDE with long input delay. Systems & Control Letters, 2009, 58(10/11): 773-782
doi: 10.1016/j.sysconle.2009.08.006 |
| [29] | 范东霞, 赵东霞, 史娜, 等. 一类扩散波方程的PDP反馈控制和稳定性分析. 数学物理学报, 2021, 41A(4): 1088-1096 |
| Fan D X, Zhao D X, Shi N, et al. The PDP feedback control and stability analysis of a diffusive wave equation. Acta Mathematica Scientia, 2021, 41A(4): 1088-1096 | |
| [30] |
Bastin G, Coron J M, D'Andrea-Novel B. On Lyapunov stability of linearised Saint-Venant equations for a sloping channel. Networks and Heterogeneous Media, 2009, 4(2): 177-187
doi: 10.3934/nhm.2009.4.177 |
| [31] |
Zhao D X, Fan D X, Guo Y P. The spectral analysis and exponential stability of a 1-d 2×2 hyperbolic system with proportional feedback control. International Journal of Control, Automation and Systems, 2022, 20(8): 2633-2640
doi: 10.1007/s12555-021-0507-0 |
| [1] | He Xuyang,Mao Mingzhi,Zhang Tengfei. Existence and Stability of a Class of Impulsive Neutral Stochastic Functional Differential Equations with Poisson Jump [J]. Acta mathematica scientia,Series A, 2023, 43(4): 1221-1243. |
| [2] | Zou Yonghui,Xu Xin. Existence of Back-Flow Point for the Two-Dimensional Compressible Prandtl Equation [J]. Acta mathematica scientia,Series A, 2023, 43(3): 691-701. |
| [3] | Yu Yang. Global Attractivity of a Nonlocal Delayed and Diffusive SVIR Model [J]. Acta mathematica scientia,Series A, 2021, 41(6): 1864-1870. |
| [4] | Dongxia Fan,Dongxia Zhao,Na Shi,Tingting Wang. The PDP Feedback Control and Stability Analysis of a Diffusive Wave Equation [J]. Acta mathematica scientia,Series A, 2021, 41(4): 1088-1096. |
| [5] | Lixiang Feng,Defen Wang. Global Stability of an Epidemic Model with Quarantine and Incomplete Treatment [J]. Acta mathematica scientia,Series A, 2021, 41(4): 1235-1248. |
| [6] | Xingshou Huang,Ricai Luo,Wusheng Wang. Stability Analysis for a Class Neural Network with Proportional Delay Based on the Gronwall Integral Inequality [J]. Acta mathematica scientia,Series A, 2020, 40(3): 824-832. |
| [7] | Zhongwei Cao,Xiangdan Wen,Wei Feng,Li Zu. Dynamics of a Nonautonomous SIRI Epidemic Model with Random Perturbations [J]. Acta mathematica scientia,Series A, 2020, 40(1): 221-233. |
| [8] | Xinzhe Zhang,Guofeng He,Gang Huang. Dynamical Properties of a Delayed Epidemic Model with Vaccination and Saturation Incidence [J]. Acta mathematica scientia,Series A, 2019, 39(5): 1247-1259. |
| [9] | Xiaojie Jing, Aimin Zhao, Guirong Liu. Global Stability of a Measles Epidemic Model with Partial Immunity and Environmental Transmission [J]. Acta mathematica scientia,Series A, 2019, 39(4): 909-917. |
| [10] | Chao Yang,Runjie Li. Existence and Stability of Periodic Solution for a Lasota-Wazewska Model with Discontinuous Harvesting [J]. Acta mathematica scientia,Series A, 2019, 39(4): 785-796. |
| [11] | Wei Fengying, Lin Qingteng. Extinction and Distribution for an SIQS Epidemic Model with Quarantined-Adjusted Incidence [J]. Acta mathematica scientia,Series A, 2017, 37(6): 1148-1161. |
| [12] | Meng Xiaoying. Analysis of a Stochastic Delayed Epidemic Model with a Non-Monotonic Incidence Rate [J]. Acta mathematica scientia,Series A, 2017, 37(6): 1162-1175. |
| [13] | Xiong Jun, Li Junmin, He Chao. Fuzzy Boundary Control Design for a Class of First-Order Hyperbolic PDEs [J]. Acta mathematica scientia,Series A, 2017, 37(3): 469-477. |
| [14] | Zhang Liping, Liu Dongyi, Zhang Guoshan. Exponential Stabilization of a Timoshenko Beam System with Internal Disturbances [J]. Acta mathematica scientia,Series A, 2017, 37(1): 185-198. |
| [15] | Wang Heyuan. The Dynamical Behaviors and the Numerical Simulation of a Five-Mode Lorenz-Like System of the MHD Equations for a Two-Dimensional Incompressible Fluid on a Torus [J]. Acta mathematica scientia,Series A, 2017, 37(1): 199-216. |
|