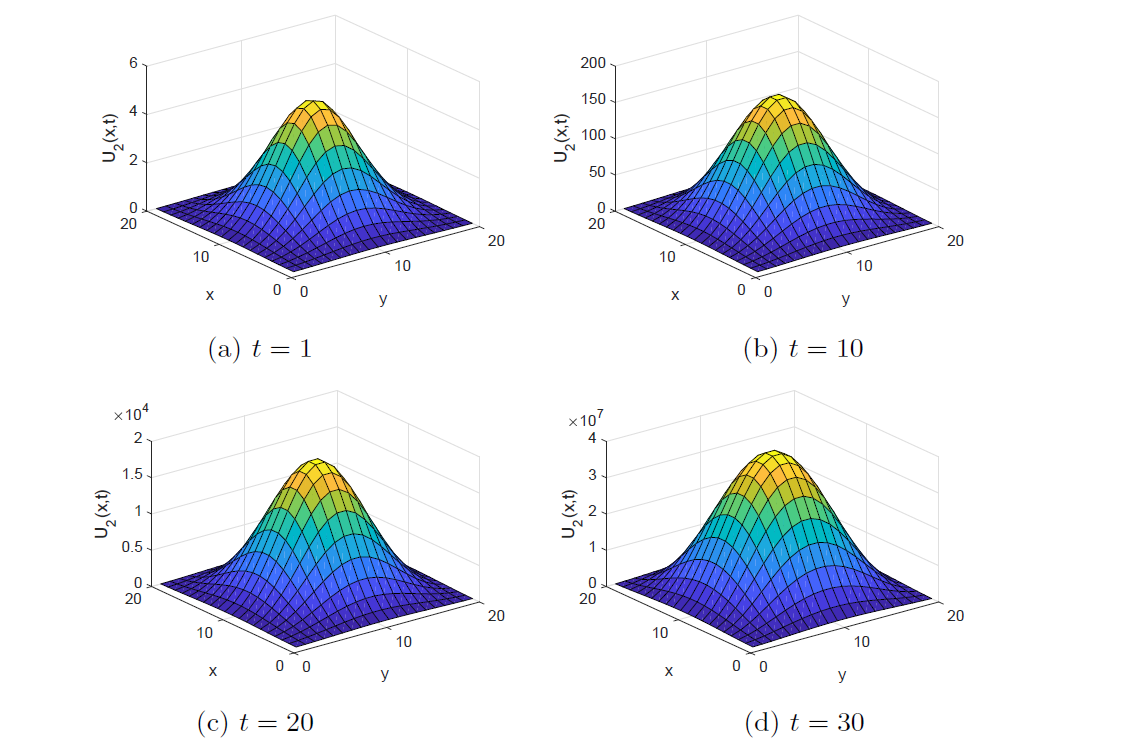
Acta mathematica scientia,Series A ›› 2023, Vol. 43 ›› Issue (3): 970-984.
Dynamical Analysis of an Age-Space Structured HIV/AIDS Model with Homogeneous Dirichlet Boundary Condition
Wu Peng1,2,*( ),Wang Xiunan3,He Zerong4
),Wang Xiunan3,He Zerong4
- 1School of Sciences, Hangzhou Dianzi University, Hangzhou 310018
2School of Data Sciences, Zhejiang University of Finance & Economics, Hangzhou 310018
3Department of Mathematics, University of Tennessee at Chattanooga, Chattanooga, TN 37403, USA
4Institute of Operational Research and Cybernetics, Hangzhou Dianzi University, Hangzhou 310018
-
Received:2022-08-03Revised:2023-02-12Online:2023-06-26Published:2023-06-01 -
Contact:Peng Wu E-mail:hzpengwu@163.com -
Supported by:NSFC(12201557);NSFC(11871185);Foundation of Zhejiang Provincial Education Department(Y202249921)
CLC Number:
- O175.1
Cite this article
Wu Peng,Wang Xiunan,He Zerong. Dynamical Analysis of an Age-Space Structured HIV/AIDS Model with Homogeneous Dirichlet Boundary Condition[J].Acta mathematica scientia,Series A, 2023, 43(3): 970-984.
share this article
| [1] | UNAIDS: AIDS by the numbers in 2020. https://www.unaids.org/en |
| [2] |
Cuadros D F, Li J, Branscum A J, et al. Mapping the spatial variability of HIV infection in Sub-Saharan Africa: Efective information for localized HIV prevention and control. Sci Rep, 2017, 7: 9093
doi: 10.1038/s41598-017-09464-y pmid: 28831171 |
| [3] |
Ayalew K A, Manda S, Cai B. A comparison of Bayesian spatial models for HIV mapping in South Africa. Int J Environ. Res Public Health, 2021, 18(21): 11215
doi: 10.3390/ijerph182111215 |
| [4] |
Wu P, Zhao H. Mathematical analysis of an age-structured HIV/AIDS epidemic model with HAART and spatial diffusion. Nonlinear Analysis: RWA, 2021, 60: 103289
doi: 10.1016/j.nonrwa.2021.103289 |
| [5] | Zhao H, Wu P, Ruan S. Dynamic analysis and optimal control three-age-class HIV/AIDS epidemic model in China. Disc Conti Dyn Syst Seri B, 2020, 25(9): 3491-3521 |
| [6] |
Wu P, Zhao H. Dynamical analysis of a nonlocal delayed and diffusive HIV latent infection model with spatial heterogeneity. J Franklin Institute, 2021, 358(10): 5552-5587
doi: 10.1016/j.jfranklin.2021.05.014 |
| [7] |
Gao Y, Wang J. Threshold dynamics of a delayed nonlocal reaction-diffusion HIV infection model with both cell-free and cell-to-cell transmissions. J Math Anal Appl, 2020, 488(1): 124047
doi: 10.1016/j.jmaa.2020.124047 |
| [8] |
Ge Q, Wang X, Rong L. A delayed reaction-diffusion viral infection model with nonlinear incidences and cell-to-cell transmission. International Journal of Biomathematics, 2021, 14(8): 2150100
doi: 10.1142/S179352452150100X |
| [9] |
Wang W, Wang X, Feng Z. Time periodic reaction-diffusion equations for modeling 2-LTR dynamics in HIV-infected patients. Nonlinear Analysis: Real World Applications, 2021, 57: 103184
doi: 10.1016/j.nonrwa.2020.103184 |
| [10] | 王晶囡, 杨德中. 具有时滞扩散效应的病原体-免疫模型的稳定性及分支. 数学物理学报, 2021, 41A(4): 1204-1217 |
| Wang J N, Yang D Z. Stability and Bifurcation analysis of a delayed diffusive pathogen-immune model. Acta Math Sci, 2021, 41A(4): 1204-1217 | |
| [11] |
Chekroun A, Kuniya T. An infection age-space structured SIR epidemic model with Neumann boundary condition. Appl Anal, 2020, 99: 1972-1985
doi: 10.1080/00036811.2018.1551997 |
| [12] |
Yang J, Xu R, Li J. Threshold dynamics of an age-space structured brucellosis disease model with Neumann boundary condition. Nonlinear Analysis: RWA, 2019, 50: 192-217
doi: 10.1016/j.nonrwa.2019.04.013 |
| [13] |
liu P, Li H. Global behavior of a multi-group SEIR epidemic model with age structure and spatial diffusion. Math Biosci Eng, 2020, 17: 7248-7273
doi: 10.3934/mbe.2020372 pmid: 33378896 |
| [14] | Wang J, Zhang R, Gao Y. Global threshold dynamics of an infection age-space structured HIV infection model with Neumann boundary condition. J Dyn Diff Equat, 2021, https://doi.org/10.1007/s10884-021-10086-2 |
| [15] |
An Q, Wang C, Wang H. Analysis of a spatial memory model with nonlocal maturation delay and hostile boundary condition. Discrete Contin Dyn Syst Ser A, 2020, 40(10): 5845-5868
doi: 10.3934/dcds.2020249 |
| [16] | Yi T, Zou X. On Dirichlet problem for a class of delayed reaction-diffusion equations with spatial non-locality. J Dyn Diff Equat, 2013 25(4): 959-979 |
| [17] |
Chekroun A, Kuniya T. Global threshold dynamics of an infection age-structured SIR epidemic model with diffusion under the Dirichlet boundary condition. J Differential Equations, 2020, 269: 117-148
doi: 10.1016/j.jde.2020.04.046 |
| [18] |
Wang X, Sun H, Yang J. Temporal-spatial analysis of an age-space structured foot-and-mouth disease model with Dirichlet boundary condition. Chaos, 2021, 31: 053120
doi: 10.1063/5.0048282 |
| [19] |
Shen M, Xiao Y, Rong L. Global stability of an infection-age structured HIV-1 model linking within-host and between-host dynamics. Math Biosci, 2015, 263: 37-50
doi: 10.1016/j.mbs.2015.02.003 pmid: 25686694 |
| [20] |
Gao Y, Wang J. Threshold dynamics of a delayed nonlocal reaction-diffusion HIV infection model with both cell-free and cell-to-cell transmissions. J Math Anal Appl, 2020, 488: 124047
doi: 10.1016/j.jmaa.2020.124047 |
| [21] |
Yang J, Jin Z, Xu F. Threshold dynamics of an age-space structured SIR model on heterogeneous environment. Appl Math Lett, 2019, 96: 69-74
doi: 10.1016/j.aml.2019.03.009 |
| [22] | Ito S. Diffusion Equations. Providence, RI: American Mathematical Society, 1992 |
| [23] |
Mckenna P J, Walter W. On the Dirichlet problem for elliptic systems. Appl Anal, 1986, 21: 207-224
doi: 10.1080/00036818608839592 |
| [24] | Protter M H, Weinberger H F. Maximum Principle in Differential Equations. New York: Springer-Verlag, 1984 |
| [25] | Wang W, Zhao X Q. Spatial invasion threshold of Lyme disease. SIAM J Appl Math, 2015 73: 1142-1170 |
| [26] | Smith H L. Monotone Dynamical Systems: An Introduction to the Theory of Competitive and Cooperative Systems. Providence, RI: American Mathematical Society, 1995 |
| [27] |
Chatelin F. The spectral approximation of linear operators with applications to the computation of eigenelements of differential and integral operators. SIAM Rev, 1981, 23: 495-522
doi: 10.1137/1023099 |
| [1] | Zhenxiang Hu,Linfei Nie. Analysis of a Reaction-Diffusion Epidemic Model with Horizontal Transmission and Environmental Transmission [J]. Acta mathematica scientia,Series A, 2022, 42(6): 1849-1860. |
| [2] | Zhanping Ma,Haifeng Huo,Hong Xiang. Dynamics and Patterns for a Diffusive Leslie-Gower Predator-Prey Model with Michaelis-Menten Type Harvesting in Prey [J]. Acta mathematica scientia,Series A, 2022, 42(5): 1575-1591. |
| [3] | Tailei Zhang,Junli Liu,Mengjie Han. Dynamics of an Anthrax Epidemiological Model with Time Delay and Seasonality [J]. Acta mathematica scientia,Series A, 2022, 42(3): 851-866. |
| [4] | Dandan Sun,Yingke Li,Zhidong Teng,Tailei Zhang. Analysis of the Stability for Measles Epidemic Model with Age-Structured [J]. Acta mathematica scientia,Series A, 2021, 41(6): 1950-1968. |
| [5] | Shuangming Wang,Xingman Fan,Mingjun Zhang,Junrong Liang. The Dynamics of an SEIR Epidemic Model with Time-Periodic Latent Period [J]. Acta mathematica scientia,Series A, 2020, 40(2): 527-539. |
| [6] | Baoyan Sun. Lower Bound of Blow-Up Time for a p-Laplacian Equation with Nonlocal Source [J]. Acta mathematica scientia,Series A, 2018, 38(5): 911-923. |
| [7] | Wu Yuanze, Wu Tsungfang, Liu Zeng. On the Brézis-Nirenberg Problem with Nonhomogeneous Dirichlet Boundary Conditions [J]. Acta mathematica scientia,Series A, 2015, 35(6): 1025-1043. |
| [8] | Gui Zhanji; Jia Jing; Ge Weigao. Global Stability of Single-species Diffusion Models with Time Delay [J]. Acta mathematica scientia,Series A, 2007, 27(3): 496-505. |
| [9] |
WEN Xian-Zhang.
The Uniform Persistence of PredatorPrey Systems with Delays [J]. Acta mathematica scientia,Series A, 2003, 23(1): 96-105. |
| Viewed | ||||||||||||||||||||||||||||||||||||||||||||||
|
Full text 166
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Abstract 128
|
|
|||||||||||||||||||||||||||||||||||||||||||||
Cited |
|
|||||||||||||||||||||||||||||||||||||||||||||
| Shared | ||||||||||||||||||||||||||||||||||||||||||||||
| Discussed | ||||||||||||||||||||||||||||||||||||||||||||||
|