Acta mathematica scientia,Series A ›› 2023, Vol. 43 ›› Issue (1): 132-142.
Previous Articles Next Articles
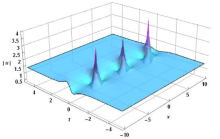
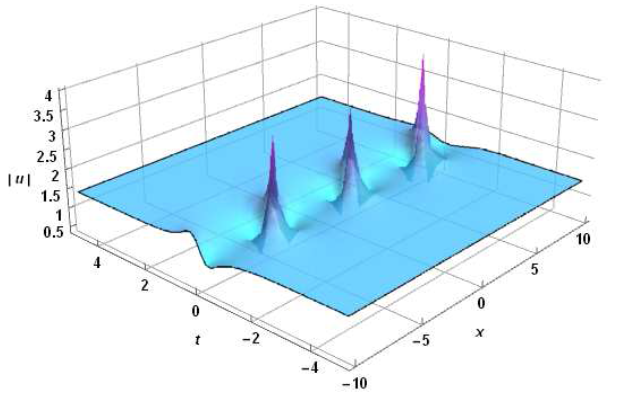
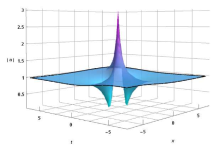
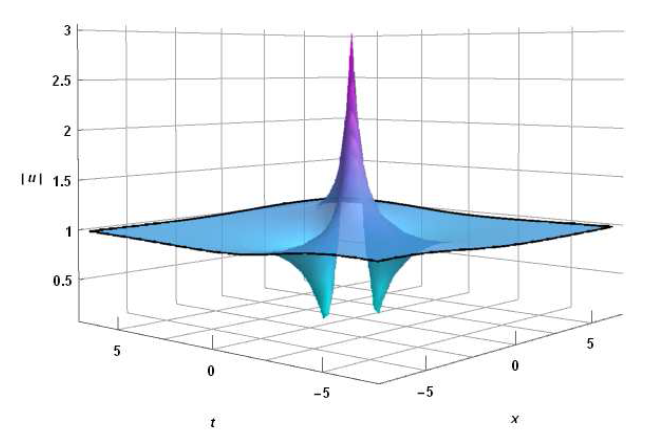
The Rogue Wave Solution of MNLS Equation Based on Hirota's Bi-linear Derivative Transformation
- School of Physics and Technology, Wuhan University, Wuhan 430072
-
Received:2022-05-15Revised:2022-08-05Online:2023-02-26Published:2023-03-07 -
Supported by:The NSFC(12074295)
CLC Number:
- O175.2
Cite this article
Tang Yuxuan, Zhou Guoquan. The Rogue Wave Solution of MNLS Equation Based on Hirota's Bi-linear Derivative Transformation[J].Acta mathematica scientia,Series A, 2023, 43(1): 132-142.
share this article
| [1] |
Akhmediev N, Ankiewicz A, Taki M. Waves that appear from nowhere and disappear without a trace. Physics Letters A, 2009, 373(6): 675-678
doi: 10.1016/j.physleta.2008.12.036 |
| [2] |
Akhmediev N, Soto-Crespo J M, Ankiewicz A. Extreme waves that appear from nowhere: on the nature of rogue waves. Physics Letters A, 2009, 373(25): 2137-2145
doi: 10.1016/j.physleta.2009.04.023 |
| [3] |
Wen X Y, Yang Y, Yan Z. Generalized perturbation      doi: 10.1103/PhysRevE.92.012917 |
| [4] |
Pan C, Bu L, Chen S, et al. General rogue wave solutions under SU (2) transformation in the vector Chen-Lee-Liu nonlinear Schrödinger equation. Physica D: Nonlinear Phenomena, 2022, 434: 133204
doi: 10.1016/j.physd.2022.133204 |
| [5] |
He J, Xu S, Cheng Y. The rational solutions of the mixed nonlinear Schrödinger equation. AIP Advances, 2015, 5(1): 017105
doi: 10.1063/1.4905701 |
| [6] |
Zhao L C, Guo B, Ling L. High-order rogue wave solutions for the coupled nonlinear Schrödinger equations-II. Journal of Mathematical Physics, 2016, 57(4): 043508
doi: 10.1063/1.4947113 |
| [7] |
Ankiewicz A, Akhmediev N. Rogue wave solutions for the infinite integrable nonlinear Schrödinger equation hierarchy. Physical Review E, 2017, 96(1): 012219
doi: 10.1103/PhysRevE.96.012219 |
| [8] |
Xu S, He J, Wang L. The Darboux transformation of the derivative nonlinear Schrödinger equation. Journal of Physics A: Mathematical and Theoretical, 2011, 44(30): 305203
doi: 10.1088/1751-8113/44/30/305203 |
| [9] |
Guo B, Ling L, Liu Q P. High-order solutions and generalized Darboux transformations of derivative nonlinear Schrödinger equations. Studies in Applied Mathematics, 2013, 130(4): 317-344
doi: 10.1111/j.1467-9590.2012.00568.x |
| [10] |
Zhang Y, Guo L, Xu S, et al. The hierarchy of higher order solutions of the derivative nonlinear Schrödinger equation. Communications in Nonlinear Science and Numerical Simulation, 2014, 19(6): 1706-1722
doi: 10.1016/j.cnsns.2013.10.005 |
| [11] |
Wang L H, Porsezian K, He J S. Breather and rogue wave solutions of a generalized nonlinear Schrödinger equation. Physical Review E, 2013, 87(5): 053202
doi: 10.1103/PhysRevE.87.053202 |
| [12] |
Lou S, Lin J. Rogue waves in nonintegrable KdV-type systems. Chinese Physics Letters, 2018, 35(5): 050202
doi: 10.1088/0256-307X/35/5/050202 |
| [13] |
Wu H, Fei J, Ma W. Lump and rational solutions for weakly coupled generalized Kadomtsev-Petviashvili equation. Modern Physics Letters B, 2021, 35(26): 2150449
doi: 10.1142/S0217984921504492 |
| [14] |
Zhou G, Li X. Space periodic solutions and rogue wave solution of the derivative nonlinear Schrödinger equation. Wuhan University Journal of Natural Sciences, 2017, 22(5): 373-379
doi: 10.1007/s11859-017-1261-2 |
| [15] |
Ma W X. Nonlocal PT-symmetric integrable equations and related Riemann-Hilbert problems. Partial Differential Equations in Applied Mathematics, 2021, 4: 100190
doi: 10.1016/j.padiff.2021.100190 |
| [16] |
Ablowitz M J, Musslimani Z H. Inverse scattering transform for the integrable nonlocal nonlinear Schrödinger equation. Nonlinearity, 2016, 29(3): 915
doi: 10.1088/0951-7715/29/3/915 |
| [17] |
Yang B, Yang J. Rogue waves in the nonlocal   doi: 10.1007/s11005-018-1133-5 |
| [18] |
Lin J, Jin X W, Gao X L, et al. Solitons on a periodic wave background of the modified KdV-Sine-Gordon equation. Communications in Theoretical Physics, 2018, 70(2): 119-126
doi: 10.1088/0253-6102/70/2/119 |
| [19] |
Li L, Duan C, Yu F. An improved Hirota bilinear method and new application for a nonlocal integrable complex modified Korteweg-de Vries (MKdV) equation. Physics Letters A, 2019, 383(14): 1578-1582
doi: 10.1016/j.physleta.2019.02.031 |
| [20] |
Zhong W P, Yang Z, Beli  doi: 10.1016/j.physleta.2021.127228 |
| [21] |
Ma W X, Zhou R. A coupled AKNS-Kaup-Newell soliton hierarchy. Journal of Mathematical Physics, 1999, 40(9): 4419-4428
doi: 10.1063/1.532976 |
| [22] |
Chen Z Y, Huang N N. Explicit N-soliton solution of the modified nonlinear Schrödinger equation. Physical Review A, 1990, 41(7): 4066-4069
doi: 10.1103/PhysRevA.41.4066 |
| [23] |
Huang N N, Chen Z Y. Alfven solitons. Journal of Physics A: Mathematical and General, 1990, 23(4): 439-453
doi: 10.1088/0305-4470/23/4/014 |
| [24] |
Chen H H, Lee Y C, Liu C S. Integrability of nonlinear Hamiltonian systems by inverse scattering method. Physica Scripta, 1979, 20(3/4): 490-492
doi: 10.1088/0031-8949/20/3-4/026 |
| [25] |
Kaup D J, Newell A C. An exact solution for a derivative nonlinear Schrödinger equation. Journal of Mathematical Physics, 1978, 19(4): 798-801
doi: 10.1063/1.523737 |
| [26] |
Kawata T, Inoue H. Exact solution of derivative nonlinear Schrödinger equation under nonvanishing conditions. J Phys Soc Jpn, 1978, 44(6): 1968-1976
doi: 10.1143/JPSJ.44.1968 |
| [27] |
Steudel H. The hierarchy of multi-soliton solutions of derivative nonlinear Schrödinger equation. J Phys A, 2003, 36: 1931-1946
doi: 10.1088/0305-4470/36/7/309 |
| [28] |
Zhou G Q, Huang N N. An  doi: 10.1088/1751-8113/40/45/008 |
| [29] |
Zhou G. A multi-soliton solution of the DNLS equation based on pure Marchenko formalism. Wuhan University Journal of Natural Sciences, 2010, 15(1): 36-42
doi: 10.1007/s11859-010-0108-x |
| [30] |
Zhou G, Bi X. Soliton solution of the DNLS equation based on Hirota's bilinear derivative transform. Wuhan University Journal of Natural Sciences, 2009, 14(6): 505-510
doi: 10.1007/s11859-009-0609-7 |
| [31] | 蔡浩. 关于MNLS方程和DNLS方程的研究. 武汉大学, 2005 |
| Cai H. Research about MNLS Equation and DNLS Equation. Wuhan Univ, 2005 | |
| [32] |
Chen X J, Lam W K. Inverse scattering transform for the derivative nonlinear Schrödinger equation with nonvanishing boundary conditions. Physical Review E, 2004, 69(6): 066604
doi: 10.1103/PhysRevE.69.066604 |
| [33] |
Chen X J, Yang J K, Lam W K.  doi: 10.1088/0305-4470/39/13/006 |
| [34] |
Lashkin V M.  doi: 10.1088/1751-8113/40/23/008 |
| [35] |
Zhou G. A newly revised inverse scattering transform for DNLS+ equation under nonvanishing boundary condition. Wuhan University Journal of Natural Sciences, 2012, 17(2): 144-150
doi: 10.1007/s11859-012-0819-2 |
| [36] |
Zhou G. Explicit breather-type and pure N-Soliton solution of DNLS+ equation with nonvanishing boundary condition. Wuhan University Journal of Natural Sciences, 2013, 18(2): 147-155
doi: 10.1007/s11859-013-0907-y |
| [37] |
Osman M S, Almusawa H, Tariq K U, et al. On global behavior for complex soliton solutions of the perturbed nonlinear Schrödinger equation in nonlinear optical fibers. Journal of Ocean Engineering and Science, 2022, 7(5): 431-443
doi: 10.1016/j.joes.2021.09.018 |
| [38] | Bourgain J. Global Solutions of Nonlinear Schrödinger Equations. Providence, RI: American Mathematical Society, 1999 |
| [1] | Jiayu Liu,Hanyu Wei,Yan Zhang,Tiecheng Xia,Hui Wang. Soliton Solutions and Its Nonlinear Dynamics Behavior Research of the Three-Component Four-Order Nonlinear Schrödinger System in Alpha Helical Protein [J]. Acta mathematica scientia,Series A, 2022, 42(6): 1873-1885. |
| [2] | Chunmei Fang,Shoufu Tian. Breather Wave Solutions, Lump Solutions and Semi-Rational Solutions of a Reduced (3+1)Dimensional Hirota Equation [J]. Acta mathematica scientia,Series A, 2022, 42(3): 775-783. |
| Viewed | ||||||||||||||||||||||||||||||||||||||||||||||
|
Full text 387
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Abstract 150
|
|
|||||||||||||||||||||||||||||||||||||||||||||
Cited |
|
|||||||||||||||||||||||||||||||||||||||||||||
| Shared | ||||||||||||||||||||||||||||||||||||||||||||||
| Discussed | ||||||||||||||||||||||||||||||||||||||||||||||
|