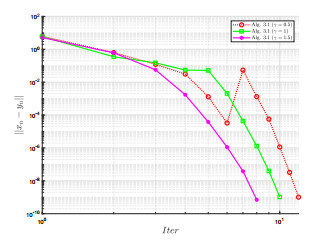
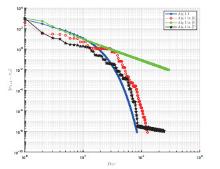
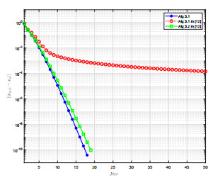
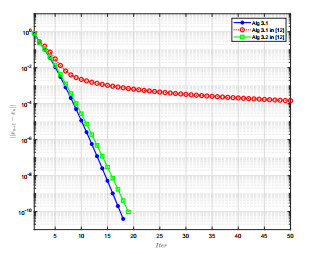
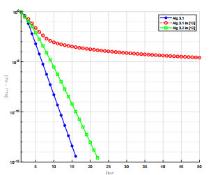
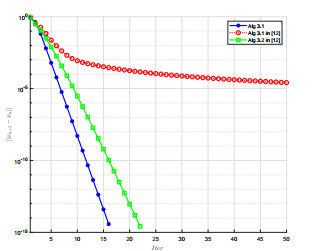
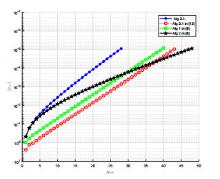
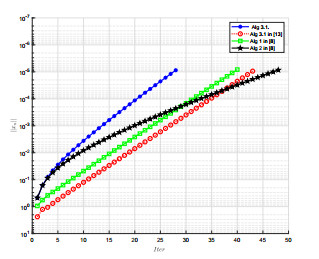
Acta mathematica scientia,Series A ›› 2022, Vol. 42 ›› Issue (3): 904-919.
Previous Articles Next Articles
A New Projection Algorithm for Solving Pseudo-Monotone Variational Inequality and Fixed Point Problems
- College of Mathematics and Statistics, Chongqing Technology and Business University, Chongqing 400067
-
Received:2021-08-12Online:2022-06-26Published:2022-05-09 -
Contact:Xianjun Long E-mail:jyang1230@163.com;xianjunlong@ctbu.edu.cn -
Supported by:NSFC(11471059);the NSF of Chongqing(cstc2021jcyj-msxmX0721);the Education Committee Project Research Foundation of Chongqing(KJZD-K201900801)
CLC Number:
- O224
Cite this article
Jing Yang,Xianjun Long. A New Projection Algorithm for Solving Pseudo-Monotone Variational Inequality and Fixed Point Problems[J].Acta mathematica scientia,Series A, 2022, 42(3): 904-919.
share this article
| 1 | Facchinei F, Pang J S. Finite-Dimensional Variational Inequalities and Complementarity Problems. New York: Springer, 2003 |
| 2 | Kinderlehrer D, Stampacchia G. An Introduction to Variational Inequalities and Their Applications. New York: Academic Press, 1980 |
| 3 |
Goldstein A A . Convex programming in Hilbert space. Bull Amer Math Soc, 1964, 70, 709- 710
doi: 10.1090/S0002-9904-1964-11178-2 |
| 4 |
Tseng P . A modified forward-backward splitting method for maximal monotone mappings. SIAM J Control Optim, 2000, 38, 431- 446
doi: 10.1137/S0363012998338806 |
| 5 | 贺月红, 龙宪军. 求解伪单调变分不等式问题的惯性收缩投影算法. 数学物理学报, 2021, 41A(6): 1897-1911 |
| He Y H, Long X J. A inertial contraction and projection algorithm for pseudomonotone variational inequality problems. 2021, 41A(6): 1897-1911 | |
| 6 | 万升联. 解变分不等式的一种二次投影算法. 数学物理学报, 2021, 41A(1): 237-244 |
| Wan S L. A double projection algorithm for solving variational inequalities. 2021, 41A(1): 237-244 | |
| 7 |
Fan J J , Qin X L . Weak and strong convergence of inertial Tseng's extragradient algorithms for solving variational inequality problems. Optimization, 2021, 70, 1195- 1216
doi: 10.1080/02331934.2020.1789129 |
| 8 |
Thong D V , Voung P T . Modified Tseng's extragradient methods for solving pseudo-monotone variational inequalities. Optimization, 2019, 68, 2207- 2226
doi: 10.1080/02331934.2019.1616191 |
| 9 |
Yang J , Liu H W . Strong convergence result for solving monotone variational inequalities in Hilbert space. Numer Algor, 2019, 80, 741- 752
doi: 10.1007/s11075-018-0504-4 |
| 10 |
Lei M , He Y R . An extragradient method for solving variational inequalities without monotonocity. J Optim Theory Appl, 2021, 188, 432- 446
doi: 10.1007/s10957-020-01791-x |
| 11 |
Thong D V , Hieu D V . Mann-type algorithms for variational inequality problems and fixed point problems. Optimization, 2020, 69, 2305- 2326
doi: 10.1080/02331934.2019.1692207 |
| 12 |
Thong D V , Hieu D V . Some extragradient-viscosity algorithms for solving variational inequality problems and fixed point problems. Numer Algor, 2019, 82, 761- 789
doi: 10.1007/s11075-018-0626-8 |
| 13 | 郭丹妮, 蔡钢. 关于变分不等式和不动点问题的新迭代算法[OL]. 数学学报(中文版), [2021-01-15]. http://kns.cnki.net/kcms/detail/11.2038.O1.20210114.1040.010.html |
| Guo D N, Cai G. A new iterative method for solving variational inequality and fixed point problems[OL]. Acta Mathematica Sinica(Chinese Series), [2021-01-15]. http://kns.cnki.net/kcms/detail/11.2038.O1.20210114.1040.010.html | |
| 14 |
Ceng L C , Shang M J . Hybrid inertial subgradient extragradient methods for variational inequalities and fixed point problems involving asymptotically nonexpansive mappings. Optimization, 2021, 70, 715- 740
doi: 10.1080/02331934.2019.1647203 |
| 15 |
Karamardian S . Complementarity problems over cones with monotone and pseudomonotone maps. J Optim Theory Appl, 1976, 18, 445- 454
doi: 10.1007/BF00932654 |
| 16 |
Chidume C E , Maruster S . Iterative methods for the computation of fixed points of demicontractive mappings. J Comput Appl Math, 2010, 234, 861- 882
doi: 10.1016/j.cam.2010.01.050 |
| 17 | Goebel K, Reich S. Uniform Convexity, Hyperbolic Geometry, and Nonexpansive Mappings. New York: Marcel Dekker, 1984 |
| 18 |
Denisov S V , Semenov V V , Chabak L M . Convergence of the modified extragradient method for variational inequalities with non-Lipschitz operators. Cybern Syst Anal, 2015, 51, 757- 765
doi: 10.1007/s10559-015-9768-z |
| 19 |
Maingé P E . A hybrid extragradient-viscosity method for monotone operators and fixed point problems. SIAM J Control Optim, 2008, 47, 1499- 1515
doi: 10.1137/060675319 |
| 20 |
Xu H K . Iterative algorithms for nonlinear operators. J Lond Math Soc, 2002, 66, 240- 256
doi: 10.1112/S0024610702003332 |
| 21 |
Cottle R W , Yao J C . Pseudo-monotone complementarity problems in Hilbert space. J Optim Theo Appl, 1992, 75, 281- 295
doi: 10.1007/BF00941468 |
| Viewed | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
Full text 171
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Abstract 135
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
Cited |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
| Shared | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Discussed | ||||||||||||||||||||||||||||||||||||||||||||||||||
|