| 1 |
马知恩, 周义仓, 王稳地, 靳帧. 传染病动力学的数学模型与研究. 北京: 科学出版社, 2004
|
|
Ma Z E , Zhou Y C , Wang W D , Jin Z . Mathematical Modeling and Research on the Dynamics of Infectious Diseases. Beijing: Science Press, 2004
|
| 2 |
王亮, 孙建兰. 麻疹流行病学研究现状. 上海医药, 2011, 32A (8): 394- 396
doi: 10.3969/j.issn.1006-1533.2011.08.010
|
|
Wang L , Sun J L . Status of epidemiology of measles. Shanghai Medical and Pharmaceutical Journal, 2011, 32A (8): 394- 396
doi: 10.3969/j.issn.1006-1533.2011.08.010
|
| 3 |
姜翠翠, 宋丽娟, 王开发. 考虑部分免疫和潜伏期的麻疹传染病模型的稳定性分析. 生物数学学报, 2017, 32A (1): 57- 64
|
|
Jiang C C , Song L J , Wang K F . Stability analysis of a measles epidemic model with partial immunity and latency. J Biomath, 2017, 32A (1): 57- 64
|
| 4 |
佘连兵. 一类具有接种的麻疹模型的动力学分析. 西南师范大学学报, 2015, 40A (7): 12- 16
|
|
She L B . On dynamical analysis of a measles model with vaccination. J Southwest Norm Univ, 2015, 40A (7): 12- 16
|
| 5 |
靖晓洁, 赵爱民, 刘桂荣. 考虑部分免疫和环境传播的麻疹传染病模型的全局稳定性. 数学物理学报, 2019, 39A (4): 909- 917
doi: 10.3969/j.issn.1003-3998.2019.04.018
|
|
Jing X J , Zhao A M , Liu A M . Global stability of a measles epidemic model with partial immunity and environmental transmission. Acta Math Sci, 2019, 39A (4): 909- 917
doi: 10.3969/j.issn.1003-3998.2019.04.018
|
| 6 |
Huang J C , Ruan S G , Wu X , Zhou X L . Seasonal transmission dynamics of measles in China. Theor Biosci, 2018, 137 (2): 185- 195
doi: 10.1007/s12064-018-0271-8
|
| 7 |
Zhou L H , Wang Y , Xiao Y Y , Li M Y . Global dynamics of a discrete age-structured SIR epidemic model with applications to measles vaccination strategies. Math Biosci, 2018, 308, 27- 37
|
| 8 |
Hale J K. Functional Differential Equations. Berlin: Springer, 1971
|
| 9 |
Webb G F. Theory of Nonlinear Age-dependent Population Dynamics. New York: Marcel Dekker, 1985
|
| 10 |
Hale J K , Waltman P . Persistence in infinite-dimensinal systems. Math, 1989, 20 (2): 388- 396
|
| 11 |
Adams R A , Fournier J J . Sobolev Spaces. New York: Academic Press, 2003
|
| 12 |
Smith H M, Thieme H R. Dynamical Systems and Population Persistence. Providence, RI: Ameri Math Soc, 2011
|
| 13 |
Diekmann O , Heesterbeek J A , Metz J A . On the definition and the couputation of the basic reproduction ratioin models for infectious diseases in heterogeneous populations. J Math Biol, 1990, 28 (4): 365- 382
|
| 14 |
Li Y Y , Nguyen L , Wang B . Comparison principles and Lipschitz regularity for some nonlinear degenerate elliptic equations. Calc Var Partial Diff, 2018, 57 (4): 1- 29
|
| 15 |
Zhao X. Dynamical Systems in Population Biology. New York: Springer-Verlag, 2003
|
| 16 |
Sigdel R P , McCluskey C . Global stability for an SEI model of infectious disease with immigration. Appl Math Comput, 2014, 243 (2): 684- 689
|
| 17 |
LaSalle G P. The Stability of Dynamical Systems. Phladelphia: SIAM, 1976
|
| 18 |
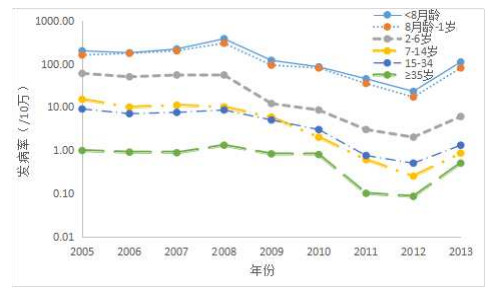
马超, 郝利新, 马静. 中国2010年麻疹流行病学特征与消除麻疹进展. 中国疫苗和免疫, 2011, 17A (3): 242- 248
|
|
Ma C , Hao L X , Ma J . Measles epidemiological characteristics and progress of measles elimination in China, 2010. Chinese Journal of Vaccines and Immunization, 2011, 17A (3): 242- 248
|
| 19 |
Duan X C , Yuan S L , Qiu Z P , Ma J L . Global stability of an epidemic model with ages of vaccination and latency. Comput Math Appl, 2014, 68, 288- 308
doi: 10.1016/j.camwa.2014.06.002
|
| 20 |
Li Y K , Teng Z D , Hu C , Ge Q . Global stability of an epidemic model with age-dependent vaccination, latent and relapse. Chaos Solit Fract, 2017, 105, 195- 207
doi: 10.1016/j.chaos.2017.10.027
|
| 21 |
陈庚. 一类具有年龄结构的传染病模型的持续性质. 高校应用数学学报, 2007, 22A (3): 253- 262
doi: 10.3969/j.issn.1000-4424.2007.03.001
|
|
Chen G . Disease persistence for a kind of age-structured epidemic models. Appl Math Ser A, 2007, 22A (3): 253- 262
doi: 10.3969/j.issn.1000-4424.2007.03.001
|
 ),Yingke Li1(
),Yingke Li1( ),Zhidong Teng2,Tailei Zhang3
),Zhidong Teng2,Tailei Zhang3