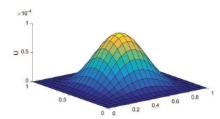
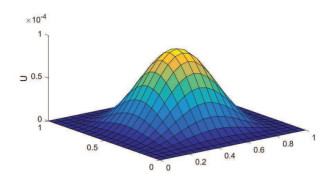
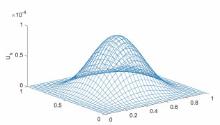
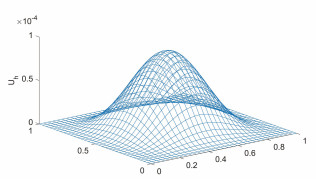
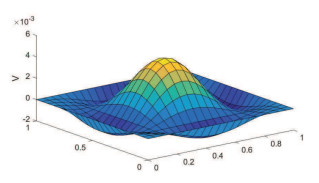
Acta mathematica scientia,Series A ›› 2021, Vol. 41 ›› Issue (6): 1880-1896.
Previous Articles Next Articles
Discontinuous Galerkin Finite Element Analysis of for the Extended Fisher-Kolmogorov Equation
- School of Mathematics and Statistics, Pingdingshan University, Henan Pingdingshan 467000
-
Received:2020-09-20Online:2021-12-26Published:2021-12-02 -
Contact:Xiaoxia Yang E-mail:yangxiaoxia1014@163.com -
Supported by:the NSFC(11271340);the NSFC(11671369);2020 Key Scientific Research Project of Henan Province Colleges and Universities(20A110030);2020 Key Scientific Research Project of Henan Province Colleges and Universities(20B110013);the Doctoral Starting Foundation of Pingdingshan University(PXY-BSQD-2019001)
CLC Number:
- O242.21
Cite this article
Xiaoxia Yang,Houchao Zhang. Discontinuous Galerkin Finite Element Analysis of for the Extended Fisher-Kolmogorov Equation[J].Acta mathematica scientia,Series A, 2021, 41(6): 1880-1896.
share this article
| 1 |
Coullet P , Elphick C , Repaux D . Nature of spatial chaos. Physical Review Letters, 1987, 58 (5): 431- 434
doi: 10.1103/PhysRevLett.58.431 |
| 2 |
Dee G T , Van Saarloos W . Bistable systems with propagating fronts leading to pattern foration. Physical Review Letters, 1988, 60 (25): 2641- 2644
doi: 10.1103/PhysRevLett.60.2641 |
| 3 |
Van Saarloos W . Dynamical velocity selection: marginal stability. Physical Review Letters, 1987, 58 (24): 2571- 2574
doi: 10.1103/PhysRevLett.58.2571 |
| 4 |
Van Saarloos W . Front propagation into unstable states: marginal stability as a dynamical mechanism for velocity selection. Physical Review A, 1988, 37 (1): 211- 229
doi: 10.1103/PhysRevA.37.211 |
| 5 |
Danumjaya P , Pani A K . Orthogonal cubic spline collocation method for the extended Fisher-Kolmogorov equation. Journal of Computational and Applied Mathematics, 2005, 174 (1): 101- 117
doi: 10.1016/j.cam.2004.04.002 |
| 6 |
Onyejekwe O . A direct implementation of a modified boundary integral formulationation for the extended Fisher-Kolmogorov equation. Journal of Applied Mathematics and Physics, 2015, 3 (10): 1262- 1269
doi: 10.4236/jamp.2015.310155 |
| 7 |
Danumjaya P . Finite element methods for one dimensional fourth order semilinear partial differential equation. International Journal of Applied and Computational Mathematics, 2016, 2 (3): 395- 410
doi: 10.1007/s40819-015-0068-0 |
| 8 | Khiari N , Omrani K . Finite difference discretization of the extended Fisher-Kolmogorov equation in two dimensions. Computers & Mathematics with Applications, 2011, 62 (11): 4151- 4160 |
| 9 | He D D . On the L∞-norm convergence of a three-level linearly implicit finite difference method for the extended Fisher-Kolmogorov equation in both 1D and 2D. Computers & Mathematics with Applications, 2016, 71 (12): 2594- 2607 |
| 10 | Liu F N, Zhao X P, Liu B. Fourier pseudo-spectral method for the extended Fisher-Kolmogorov equation in two dimensions. Advances in Difference Equations, 2017, Article number: 94 |
| 11 | Danumjaya P , Pani A K . Numerical methods for the extended Fisher-Kolmogorov(EFK) equation. International Journal of Numerical Analysis and Modeling, 2006, 3 (2): 186- 210 |
| 12 |
Danumjaya P , Pani A K . Mixed finite element methods for a fourth order reaction diffusion equation. Numerical Methods for Partial Differential Equations, 2012, 28 (4): 1227- 1251
doi: 10.1002/num.20679 |
| 13 | Wang J F , Li H , Siriguleng H , et al. A new linearized Crank-Nicolson mixed element scheme for the extended Fisher-Kolmogorov equation. The Scientific World Journal, 2013, 2013 (1): 202- 212 |
| 14 | 张厚超, 王俊俊, 石东洋. Extended Fisher-Kolmogorov方程的一类低阶非协调混合有限元方法. 数学物理学报, 2018, 38A (3): 571- 587 |
| Zhang H C , Wang J J , Shi D Y . A type of new lower order nonconforming mixed finite elements methods for the extended Fisher-Kolmogorov equation. Acta Mathematica Scientia, 2018, 38A (3): 571- 587 | |
| 15 | 张厚超, 石东洋. EFK方程一个新的低阶非协调混合有限元方法的高精度分析. 高校应用数学学报, 2017, 32A (4): 437- 454 |
| Zhang H C , Shi D Y . High accuracy analysis of a new low order nonconforming mixed finite element method for the EFK equation. Applied Mathematics: A Journal of Chinese Universities, 2017, 32A (4): 437- 454 | |
| 16 | 石钟慈. 关于Wilson元的最佳收敛阶. 计算数学, 1986, (2): 159- 163 |
| Shi Z C . A remark on the optimal order of convergence of Wilson's nonconforming element. Mathematica Numerica Sinica, 1986, (2): 159- 163 | |
| 17 |
Shi Z C . A convergengce condition for the quadrilateral Wilson element. Numerische Mathematik, 1984, 44 (3): 349- 361
doi: 10.1007/BF01405567 |
| 18 | 江金生, 程晓良. 二阶问题的一个类Wilson非协调元. 计算数学, 1992, (3): 274- 278 |
| Jiang J S , Cheng X L . A nonconforming element like wilson's for second-order problems. Mathematica Numerica Sinica, 1992, (3): 274- 278 | |
| 19 |
Chen S C , Shi D Y . Accuracy analysis for quasi-Wilson element. Acta Mathematica Scientia, 2000, 20 (1): 44- 48
doi: 10.1016/S0252-9602(17)30730-0 |
| 20 |
Shi D Y , Zhang D . Approximation of nonconforming Quasi-Wilson element for Sine-Gordon equations. Journal of Computational Mathematics, 2013, 31 (3): 271- 282
doi: 10.4208/jcm.1212-m3897 |
| 21 | Shi D Y , Zhao Y M , Wang F L . Quasi-Wilson nonconforming element approximation for nonlinear dual phase lagging heat conduction equations. Applied Mathematics and Computation, 2014, 243 (17): 454- 464 |
| 22 |
Shi D Y , Wang F L , Zhao Y M . Superconvergence analysis and extrapolation of quasi-Wilson nonconforming finite element method for nonlinear Sobolev equations. Acta Mathematicae Applicatae Sinica, 2013, 29 (2): 403- 414
doi: 10.1007/s10255-013-0216-4 |
| 23 |
Shi D Y , Pei L F . Nonconforming quadrilateral finite element method for a class of nonlinear sine-Gordon equations. Applied Mathematics and Computation, 2013, 219 (17): 9447- 9460
doi: 10.1016/j.amc.2013.03.008 |
| 24 | 宋士仓, 苏恒迪, 雷蕾. Wilson元求解二阶椭圆问题的一种新格式. 高等学校计算数学学报, 2015, 37 (2): 156- 165 |
| Song S C , Su H D , Lei L . A new scheme of wilson element for second-order elliptic problems. Numerical Mathematics: A Journal of Chinese Universities, 2015, 37 (2): 156- 165 | |
| 25 |
Song S C , Sun M , Jiang L Y . A nonconforming scheme to solve the parabolic problem. Applied Mathematics and Computation, 2015, 265, 108- 119
doi: 10.1016/j.amc.2015.04.089 |
| 26 | Douglas J, Dupont T. Interior Penalty Procedures for Elliptic and Parabolic Galerkin Methods. Berlin: Springer, 1976 |
| 27 | 杨晓侠, 李永献. 黏弹性方程的Wilson元收敛性分析. 应用数学, 2018, 31 (3): 513- 521 |
| Yang X X , Li Y X . Convergence analysis of Wilson element for viscoelasticity type equations. Mathematica Applicata, 2018, 31 (3): 513- 521 | |
| 28 | 梁聪刚, 杨晓侠, 石东洋. 抛物积分微分方程的Wilson元收敛性分析. 数学物理学报, 2019, 39A (5): 1158- 1169 |
| Liang C G , Yang X X , Shi D Y . Convergence analysis of Wilson element for parabolic integro-differential equation. Acta Mathematica Scientia, 2019, 39A (5): 1158- 1169 | |
| 29 |
Shi D Y , Ren J C . Nonconforming mixed finite element approximation to the stationary Navier-Stokes equations on anisotropic meshes. Nonlinear Analysis: TMA, 2009, 71 (9): 3842- 3852
doi: 10.1016/j.na.2009.02.047 |
| 30 | Hale J K. Ordinary Diffrential Equations. New York: Wiley-Interscience, 1969 |
| 31 | 张铁. 间断有限元理论与方法. 北京: 科学出版社, 2012 |
| Zhang T . The Theory and Method of Discotinuous Finite Element. Beijing: Science Press, 2012 | |
| 32 | 孟雄, 舒期望, 杨扬. 发展型偏微分方程间断有限元方法的超收敛性. 中国科学, 2015, 45 (7): 1041- 1060 |
| Meng X , Shu Q W , Yang Y . Superconvergence of discontinuous Galerkin methods for time-dependent partial differential equations. Scientia Sinica Mathematica, 2015, 45 (7): 1041- 1060 | |
| 33 | 曹外香, 张智民. 解一维双曲守恒律方程和抛物方程的间断有限元法的逐点和区间平均值误差估计. 中国科学, 2015, 45 (8): 1115- 1132 |
| Cao W X , Zhang Z M . Point-wise and cell average error estimates of the DG and LDG methods for 1D hyperbolic and parabolic equations. Scientia Sinica Mathematica, 2015, 45 (8): 1115- 1132 |
| [1] | He Yuehong, Long Xianjun. A Inertial Contraction and Projection Algorithm for Pseudomonotone Variational Inequality Problems [J]. Acta mathematica scientia,Series A, 2021, 41(6): 1897-1911. |
| [2] | Zhibin Zhu,Yuanhang Geng. A Modified Three-Term WYL Conjugate Gradient Method [J]. Acta mathematica scientia,Series A, 2021, 41(6): 1871-1879. |
| [3] | Haiyun Deng,Hui Liu,Wenjing Song. Finite Difference Scheme for the Nonhomogeneous Initial Boundary Value Problem of Critical Schrödinger Map [J]. Acta mathematica scientia,Series A, 2021, 41(5): 1311-1322. |
| [4] | Yiyuan Cheng,Xingxing Zha,Yongquan Zhang. On Stochastic Accelerated Gradient with Convergence Rate of Regression Learning [J]. Acta mathematica scientia,Series A, 2021, 41(5): 1574-1584. |
| [5] | Huaxin Chen,Wensheng Jia. Approximation Theorem and General Convergence of Population Games [J]. Acta mathematica scientia,Series A, 2021, 41(5): 1566-1573. |
| [6] | Yajun Xie. A Class of Efficient Modified Algorithms Based onHalley-Newton Methods [J]. Acta mathematica scientia,Series A, 2021, 41(4): 1066-1078. |
| [7] | Qiulan Qi,Dandan Guo. Approximation Properties of a New Bernstein-Bézier Operators with Parameters [J]. Acta mathematica scientia,Series A, 2021, 41(3): 583-594. |
| [8] | Guodong Ma. Improved PRP and HS Conjugate Gradient Methods with the Strong Wolfe Line Search [J]. Acta mathematica scientia,Series A, 2021, 41(3): 837-847. |
| [9] | Xiaoni Chi,Rong Zeng,Sanyang Liu,Zhibin Zhu. A Regularized Nonmonotone Inexact Smoothing Newton Algorithm for Weighted Symmetric Cone Complementarity Problems [J]. Acta mathematica scientia,Series A, 2021, 41(2): 507-522. |
| [10] | Juan Wang,Jie Zhao. Homogenization of the Oscillating Robin Mixed Boundary Value Problems [J]. Acta mathematica scientia,Series A, 2021, 41(1): 81-90. |
| [11] | Shenglian Wan. A Double Projection Algorithm for Solving Variational Inequalities [J]. Acta mathematica scientia,Series A, 2021, 41(1): 237-244. |
| [12] | Bing Meng,Dingcheng Wang,Qunying Wu. On the Complete Moment Convergence for Weighted Sums of Rowwise Asymptotically Almost Negatively Associated Random Variables [J]. Acta mathematica scientia,Series A, 2020, 40(6): 1670-1681. |
| [13] | Juan Wang,Zixia Yuan. Global Existence and Convergence of Solutions to a Chemotactic Model with Logarithmic Sensitivity and Mixed Boundary Conditions [J]. Acta mathematica scientia,Series A, 2020, 40(6): 1646-1669. |
| [14] | Zhihao Ge,Ruihua Li. Numerical Methods for the Critical Temperature and Gap Solution of Bogoliubov-Tolmachev-Shirkov Model [J]. Acta mathematica scientia,Series A, 2020, 40(6): 1699-1711. |
| [15] | Zhihong Zhao,Yingzhen Lin. Reproducing Kernel Method for Piecewise Smooth Boundary Value Problems [J]. Acta mathematica scientia,Series A, 2020, 40(5): 1333-1340. |
| Viewed | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
Full text 152
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Abstract 132
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
Cited |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
| Shared | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Discussed | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
||