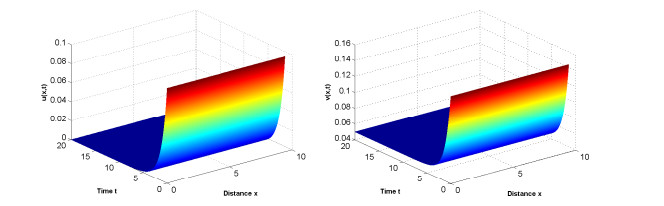
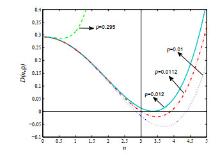
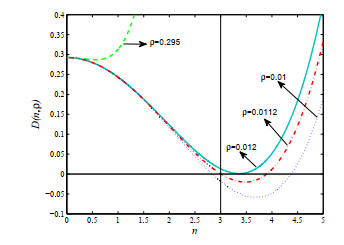
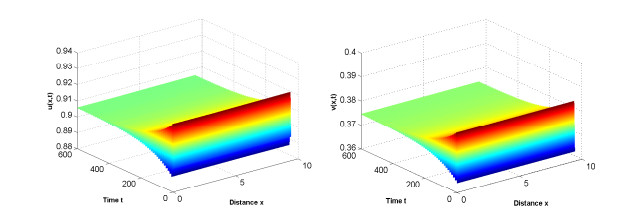
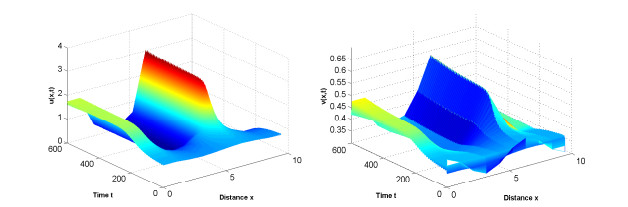
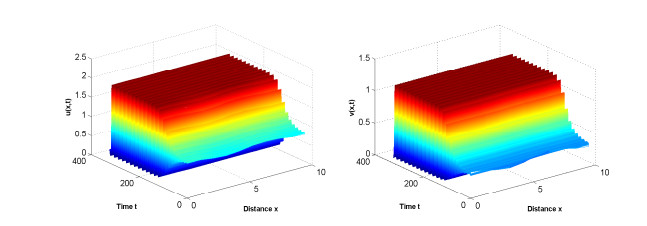
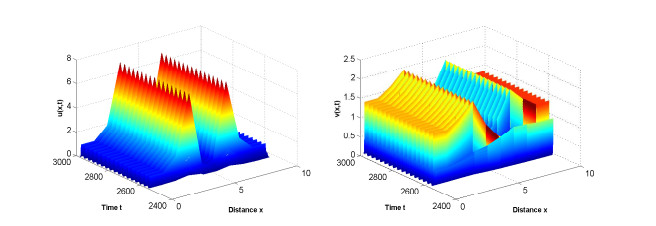
Acta mathematica scientia,Series A ›› 2021, Vol. 41 ›› Issue (4): 1204-1217.
Previous Articles Next Articles
Stability and Bifurcation of a Pathogen-Immune Model with Delay and Diffusion Effects
- Department of Applied Mathematics, Harbin University of Science and Technology, Harbin 150080
-
Received:2019-09-28Online:2021-08-26Published:2021-08-09 -
Contact:Jingnan Wang E-mail:wangjingnan@hrbust.edu.cn -
Supported by:the NSFC(11801122);the NSF of Heilongjiang Province(A2018008)
CLC Number:
- O175.29
Cite this article
Jingnan Wang,Dezhong Yang. Stability and Bifurcation of a Pathogen-Immune Model with Delay and Diffusion Effects[J].Acta mathematica scientia,Series A, 2021, 41(4): 1204-1217.
share this article
| 1 | Naheed A , Singh M , Lucy D . Numerical study of SARS epidemic model with the inclusion of diffusion in the system. Appl Math Comput, 2014, 229, 480- 498 |
| 2 |
Beauchemin C A A , Handel A . A review of mathematical models of influenza a infections within a host or cell culture: lessons learned and challenges ahead. BMC Public Health, 2011, 11 (Suppl 1): S7
doi: 10.1186/1471-2458-11-S1-S7 |
| 3 |
韩祥临, 汪维刚, 莫嘉琪. 流行性病毒传播生态动力学系统. 数学物理学报, 2019, 39A (1): 200- 208
doi: 10.3969/j.issn.1003-3998.2019.01.019 |
|
Han X L , Wang W G , Mo J Q . Bionomics dynamic system for epidemic virus transmission. Acta Math Sci, 2019, 39A (1): 200- 208
doi: 10.3969/j.issn.1003-3998.2019.01.019 |
|
| 4 | 唐三一, 唐彪, BragazziN L, 等. 新型冠状病毒肺炎疫情数据挖掘与离散随机传播动力学模型分析. 中国科学: 数学, 2020, 50 (8): 1071- 1086 |
| Tang S Y , Tang B , Bragazzi N L , et al. Analysis of COVID-19 epidemic traced data and stochastic discrete transmission dynamic model. Sci Sin Math, 2020, 50 (8): 1071- 1086 | |
| 5 |
程欣欣, 饶亚情, 黄刚. 封闭空间中新型冠状病毒肺炎传播模型: 以日本"钻石公主号"邮轮为例. 数学物理学报, 2020, 40A (2): 540- 544
doi: 10.3969/j.issn.1003-3998.2020.02.024 |
|
Cheng X X , Rao Y Q , Huang G . COVID-19 transmission model in an enclosed space: a case study of Japan Diamond Princess Cruises. Acta Math Sci, 2020, 40A (2): 540- 544
doi: 10.3969/j.issn.1003-3998.2020.02.024 |
|
| 6 |
Gilchrist M A , Sasaki A . Modeling host-parasite coevolution: a nested approach based on mechanistic models. J Theor Biol, 2002, 218 (3): 289- 308
doi: 10.1006/jtbi.2002.3076 |
| 7 |
Mohtashemi M , Levins R . Transient dynamics and early diagnostics in infectious disease. J Math Biol, 2001, 43 (5): 446- 470
doi: 10.1007/s002850100103 |
| 8 | Pugliese A , Gandolfi A . A simple model of pathogen-immune dynamics including specific and non-specific immunity. Math Biosci, 2008, 214 (1): 73- 80 |
| 9 | Wang W , Ma W . Hepatitis C virus infection is blocked by HMGB1: a new nonlocal and time-delayed reaction-diffusion model. Appl Math Comput, 2018, 320, 633- 653 |
| 10 |
Stancevic O , Angstmann C N , Murray J M , et al. Turing patterns from dynamics of early HIV infection. B Math Biol, 2013, 75 (5): 774- 795
doi: 10.1007/s11538-013-9834-5 |
| 11 |
Lee M R , Huang Y T , Lee P I , et al. Healthcare-associated bacteraemia caused by Leuconostoc species at a university hospital in Taiwan between 1995 and 2008. J Hosp Infect, 2011, 78 (1): 45- 49
doi: 10.1016/j.jhin.2010.11.014 |
| 12 |
崔青曼, 袁春营, 李春岭, 等. 主要海水养殖鱼类白点病和盾纤毛虫病防治技术. 水利渔业, 2007, 27 (6): 85- 87
doi: 10.3969/j.issn.1003-1278.2007.06.037 |
|
Cui Q M , Yuan C Y , Li C L , et al. Control of white - spot disease and scuticociliatida disease of some main cultured sea fishes. Reservoir Fisheries, 2007, 27 (6): 85- 87
doi: 10.3969/j.issn.1003-1278.2007.06.037 |
|
| 13 | 孙汶生. 医学免疫学. 北京: 高等教出版社, 2010 |
| Sun W S . Medical Immunology. Bei Jing: Higher Education Press, 2010 | |
| 14 | Han X L , Jin Z . A dynamic model of hepatitis B virus with delayed immune response. J North University of China, 2011, 32 (1): 197- 208 |
| 15 |
Bai Z , Peng R , Zhao X Q . A reaction-diffusion malaria model with seasonality and incubation period. J Math Biol, 2018, 77 (1): 201- 228
doi: 10.1007/s00285-017-1193-7 |
| 16 |
Zhu D D , Ren J L , Zhu H P . Spatial-temporal basic reproduction number and dynamics for a dengue disease diffusion model for a dengue disease diffusion model. Math Meth Appl Sci, 2018, 41, 5388- 5403
doi: 10.1002/mma.5085 |
| 17 |
Yamazaki K . Threshold dynamics of reaction-diffusion partial differential equations model of Ebola virus disease. Int J Biomath, 2018, 11 (8): 1850108
doi: 10.1142/S1793524518501085 |
| 18 |
Diggles B K , Lester R J G . Influence of temperature and host species on the development of cryptocaryon irritans. J Parasitol, 1996, 82 (1): 45- 51
doi: 10.2307/3284114 |
| 19 |
Wang K , Wang W , Pang H , et al. Complex dynamic behavior in a viral model with delayed immune response. Physica D, 2007, 226 (2): 197- 208
doi: 10.1016/j.physd.2006.12.001 |
| 20 |
Xie Q , Huang D , Zhang S , et al. Analysis of a viral infection model with delayed immune response. Appl Math Model, 2010, 34 (9): 2388- 2395
doi: 10.1016/j.apm.2009.11.005 |
| 21 |
Niu B , Guo Y X , Du Y F . Hopf bifurcation induced by delay effect in a diffusive tumor-immune system. Int J Bifurcat Chaos, 2018, 28 (11): 1850136
doi: 10.1142/S0218127418501365 |
| 22 | Canabarro A A , Gléria I M , Lyra M L . Periodic solutions and chaos in a nonlinear model for the delayed cellular immune response. Physica A, 2004, 342 (1/2): 234- 241 |
| 23 | Wu J H . Theory and Applications of Partial Functional Differential Equations. New York: Springer-Verlag, 1996 |
| 24 |
Jiang W , Wang H , Cao X . Turing instability and Turing-Hopf bifurcation in diffusive Schnakenberg systems with gene expression time delay. J Dynam Differential Equations, 2019, 31 (4): 2223- 2247
doi: 10.1007/s10884-018-9702-y |
| 25 |
Wang W , Liu Q X , Jin Z . Spatiotemporal complexity of a ratio-dependent predator-prey system. Phys Rev E, 2007, 75 (5): 051913
doi: 10.1103/PhysRevE.75.051913 |
| 26 |
Baurmann M , Gross T , Feudel U . Instabilities in spatially extended predator-prey systems: spatio-temporal patterns in the neighborhood of Turing-Hopf bifurcations. J Theor Biol, 2007, 245 (2): 220- 229
doi: 10.1016/j.jtbi.2006.09.036 |
| 27 |
Song Y , Jiang H , Liu Q X , et al. Spatiotemporal dynamics of the diffusive Mussel-Algae model near Turing-Hopf bifurcation. SIAM J on Appl Dyn Syst, 2017, 16 (4): 2030- 2062
doi: 10.1137/16M1097560 |
| 28 |
Garvie M R . Finite-difference schemes for reaction-diffusion equations modeling predator-prey interactions in MATLAB. B Math Biol, 2007, 69 (3): 931- 956
doi: 10.1007/s11538-006-9062-3 |
| [1] | Zhiyu Zhang. Oscillation Criteria of Second-Order Generalized Emden-Fowler Delay Differential Equations with a Sub-Linear Neutral Term [J]. Acta mathematica scientia,Series A, 2021, 41(3): 811-826. |
| [2] | Xiling Li,Fei Gao,Wenqin Li. Stability Analysis of Fractional-Order Hepatitis B Virus Infection Model With Immune Delay [J]. Acta mathematica scientia,Series A, 2021, 41(2): 562-576. |
| [3] | Gaihui Guo,Xiaohui Liu. Hopf Bifurcation and Stability for an Autocatalytic Reversible Biochemical Reaction Model [J]. Acta mathematica scientia,Series A, 2021, 41(1): 166-177. |
| [4] | Kaixuan Zhu,Yongqin Xie,Feng Zhou,Xijun Deng. Pullback Attractors for the Complex Ginzburg-Landau Equations with Delays [J]. Acta mathematica scientia,Series A, 2020, 40(5): 1341-1353. |
| [5] | Jian Liu,Zhixin Zhang,Wei Jiang. Global Mittag-Leffler Stability of Fractional Order Nonlinear Impulsive Differential Systems with Time Delay [J]. Acta mathematica scientia,Series A, 2020, 40(4): 1053-1060. |
| [6] | Xingshou Huang,Ricai Luo,Wusheng Wang. Stability Analysis for a Class Neural Network with Proportional Delay Based on the Gronwall Integral Inequality [J]. Acta mathematica scientia,Series A, 2020, 40(3): 824-832. |
| [7] | Xiaoxiao Zhang,Hua Dong. Dividend Problem with Parisian Delay for the Classical Risk Model with Debit Interest [J]. Acta mathematica scientia,Series A, 2019, 39(5): 1272-1280. |
| [8] | Jimeng Li. Oscillation Analysis of Second-Order Generalized Emden-Fowler-Type Delay Differential Equations [J]. Acta mathematica scientia,Series A, 2019, 39(5): 1041-1054. |
| [9] | Chao Yang,Runjie Li. Existence and Stability of Periodic Solution for a Lasota-Wazewska Model with Discontinuous Harvesting [J]. Acta mathematica scientia,Series A, 2019, 39(4): 785-796. |
| [10] | Qinghua Zhou,Li Wan,Jie Liu. Global Attracting Set for Neutral Type Hopfield Neural Networks with Time-Varying Delays [J]. Acta mathematica scientia,Series A, 2019, 39(4): 823-831. |
| [11] | Wenjuan Li,Shuhai Li,Yuanhong Yu. Oscillation of Second Order Nonlinear Neutral Differential Equations with Distributed Delay [J]. Acta mathematica scientia,Series A, 2019, 39(4): 812-822. |
| [12] | Qiong Wang,Fang Long,Jun Wang. Some Results on Difference Riccati Equations and Delay Differential Equations [J]. Acta mathematica scientia,Series A, 2019, 39(4): 832-838. |
| [13] | Zhang Wanlu, Yin Xiaolong, Zhao Xianghua. On the Occupation Times in a Dual Delayed Sparre Andersen Risk Model [J]. Acta mathematica scientia,Series A, 2019, 39(4): 918-931. |
| [14] | Gengen Zhang,Wansheng Wang,Aiguo Xiao. Asymptotic Estimation of the Trapezoidal Method for a Class of Neutral Differential Equation with Variable Delay [J]. Acta mathematica scientia,Series A, 2019, 39(3): 560-569. |
| [15] | Haiyin Li. Hopf Bifurcation of Delayed Density-Dependent Predator-Prey Model [J]. Acta mathematica scientia,Series A, 2019, 39(2): 358-371. |
| Viewed | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
Full text 417
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Abstract 96
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
Cited |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
| Shared | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Discussed | ||||||||||||||||||||||||||||||||||||||||||||||||||
|