Acta mathematica scientia,Series A ›› 2021, Vol. 41 ›› Issue (4): 1166-1180.
Previous Articles Next Articles
The Performance Analysis of the M/G/1 Queue with Multiple Adaptive Vacations under the Modified Dyadic Min(N,D)-Policy
Min Wang1( ),Yinghui Tang1,*(
),Yinghui Tang1,*( ),Shaojun Lan2,*(
),Shaojun Lan2,*( )
)
- 1 School of Mathematical Science, Sichuan Normal University, Chengdu 610066
2 School of Mathematics and Statistics, Sichuan University of Science and Engineering, Sichuan Zigong 643000
-
Received:2019-03-19Online:2021-08-26Published:2021-08-09 -
Contact:Yinghui Tang,Shaojun Lan E-mail:767076057@qq.com;tangyh@sicnu.edu.cn;sjlan89@163.com -
Supported by:the NSFC(71571127)
CLC Number:
- O226
Cite this article
Min Wang,Yinghui Tang,Shaojun Lan. The Performance Analysis of the M/G/1 Queue with Multiple Adaptive Vacations under the Modified Dyadic Min(N,D)-Policy[J].Acta mathematica scientia,Series A, 2021, 41(4): 1166-1180.
share this article
"
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 1 | 30.0000 | 25.8207 | 25.4800 | 25.4615 | 25.4614 | 25.4615 | 25.4615 |
| 5 | 30.0000 | 21.8145 | 20.5209 | 20.4796 | 20.6078 | 20.6890 | 20.7213 |
| 9 | 30.0000 | 21.2398 | 19.6983 | 19.7409 | 20.1381 | 20.5002 | 20.7321 |
| 12 | 30.0000 | 21.1440 | 19.5367 | 19.6127 | 20.1577 | 20.7372 | 21.1888 |
| 18 | 30.0000 | 21.1069 | 19.4623 | 19.5593 | 20.2405 | 21.0868 | 21.8986 |
| 23 | 30.0000 | 21.1037 | 19.4542 | 19.5541 | 20.2671 | 21.1978 | 22.1613 |
| 31 | 30.0000 | 21.1032 | 19.4527 | 19.5533 | 20.2762 | 21.2409 | 22.2819 |
| 32 | 30.0000 | 21.1032 | 19.4527 | 19.5533 | 20.2764 | 21.2424 | 22.2864 |
| 33 | 30.0000 | 21.1032 | 19.4527 | 19.5533 | 20.2766 | 21.2434 | 22.2900 |
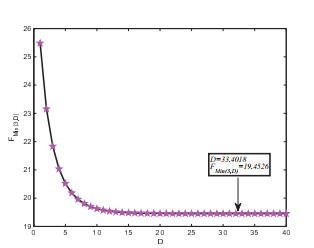
| 33.4013 | 30.0000 | 21.1032 | 19.4527 | 19.5533 | 20.2767 | 21.2438 | 22.2912 |
| 33.4017 | 30.0000 | 21.1032 | 19.4527 | 19.5533 | 20.2767 | 21.2438 | 22.2912 |
| 33.4018 | 30.0000 | 21.1032 | 19.5533 | 20.2767 | 21.2438 | 22.2912 | |
| 33.41 | 30.0000 | 21.1032 | 19.4526 | 19.5533 | 20.2767 | 21.2438 | 22.2912 |
| 33.7 | 30.0000 | 21.1032 | 19.4526 | 19.5533 | 20.2767 | 21.2440 | 22.2920 |
| 38 | 30.0000 | 21.1032 | 19.4526 | 19.5533 | 20.2770 | 21.2459 | 22.2987 |
"
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||
| 1 | 26.2741 | 25.7841 | 25.7052 | 25.6922 | 25.6900 | 25.6896 | 25.6896 | 25.6896 |
| 5 | 22.4964 | 21.7610 | 21.6467 | 21.6279 | 21.6248 | 21.6243 | 21.6242 | 21.6242 |
| 9 | 21.9370 | 21.1854 | 21.0692 | 21.0501 | 21.0469 | 21.0464 | 21.0463 | 21.0463 |
| 13 | 21.8300 | 21.0759 | 20.9595 | 20.9403 | 20.9372 | 20.9366 | 20.9365 | 20.9365 |
| 18 | 21.8069 | 21.0523 | 20.9358 | 20.9166 | 20.9134 | 20.9129 | 20.9128 | 20.9128 |
| 23 | 21.8038 | 21.0491 | 20.9326 | 20.9134 | 20.9102 | 20.9097 | 20.9096 | 20.9096 |
| 28 | 21.8033 | 21.0487 | 20.9322 | 20.9130 | 20.9098 | 20.9093 | 20.9092 | 20.9092 |
| 29 | 21.8033 | 21.0486 | 20.9321 | 20.9130 | 20.9098 | 20.9092 | 20.9092 | 20.9091 |
| 29.2348 | 21.8033 | 21.0486 | 20.9321 | 20.9130 | 20.9098 | 20.9092 | 20.9092 | 20.9091 |
| 29.2349 | 21.8033 | 21.0486 | 20.9321 | 20.9130 | 20.9098 | 20.9092 | 20.9091 | |
| 29.235 | 21.8033 | 21.0486 | 20.9321 | 20.9130 | 20.9098 | 20.9092 | 20.9091 | 20.9091 |
| 31 | 21.8033 | 21.0486 | 20.9321 | 20.9129 | 20.9097 | 20.9092 | 20.9091 | 20.9091 |
| 32 | 21.8033 | 21.0486 | 20.9321 | 20.9129 | 20.9097 | 20.9092 | 20.9091 | 20.9091 |
"
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 1 | 25.9566 | 25.4416 | 25.3591 | 25.3455 | 25.3432 | 25.3428 | 25.3428 | 25.3427 |
| 5 | 21.1710 | 20.4708 | 20.3642 | 20.3467 | 20.3437 | 20.3433 | 20.3432 | 20.3432 |
| 9 | 20.3280 | 19.6502 | 19.5480 | 19.5312 | 19.5284 | 19.5280 | 19.5279 | 19.5279 |
| 13 | 20.1331 | 19.4640 | 19.3633 | 19.3468 | 19.3441 | 19.3436 | 19.3435 | 19.3435 |
| 18 | 20.0815 | 19.4151 | 19.3149 | 19.2985 | 19.2958 | 19.2953 | 19.2952 | 19.2952 |
| 23 | 20.0729 | 19.4070 | 19.3069 | 19.2905 | 19.2878 | 19.2873 | 19.2873 | 19.2872 |
| 28 | 20.0715 | 19.4057 | 19.3056 | 19.2892 | 19.2865 | 19.2860 | 19.2860 | 19.2860 |
| 33 | 20.0713 | 19.4055 | 19.3054 | 19.2890 | 19.2863 | 19.2858 | 19.2858 | 19.2858 |
| 34 | 20.0713 | 19.4055 | 19.3054 | 19.2890 | 19.2863 | 19.2858 | 19.2858 | 19.2857 |
| 34.53 | 20.0713 | 19.4055 | 19.3054 | 19.2890 | 19.2863 | 19.2858 | 19.2858 | 19.2857 |
| 34.5301 | 20.0713 | 19.4055 | 19.3054 | 19.2890 | 19.2863 | 19.2858 | 19.2857 | |
| 34.5302 | 20.0713 | 19.4055 | 19.3054 | 19.2890 | 19.2863 | 19.2858 | 19.2857 | 19.2857 |
| 34.9 | 20.0713 | 19.4055 | 19.3054 | 19.2890 | 19.2863 | 19.2858 | 19.2857 | 19.2857 |
| 35 | 20.0713 | 19.4055 | 19.3054 | 19.2890 | 19.2863 | 19.2858 | 19.2857 | 19.2857 |
"
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 1 | 25.9386 | 25.4231 | 25.3406 | 25.3269 | 25.3247 | 25.3243 | 25.3242 | 25.3242 |
| 5 | 21.0841 | 20.4333 | 20.3349 | 20.3187 | 20.3160 | 20.3156 | 20.3155 | 20.3155 |
| 9 | 20.2842 | 19.6997 | 19.6125 | 19.5983 | 19.5959 | 19.5955 | 19.5954 | 19.5954 |
| 13 | 20.1117 | 19.5548 | 19.4721 | 19.4585 | 19.4563 | 19.4559 | 19.4558 | 19.4558 |
| 18 | 20.0675 | 19.5210 | 19.4399 | 19.4266 | 19.4244 | 19.4241 | 19.4240 | 19.4240 |
| 23 | 20.0602 | 19.5160 | 19.4353 | 19.4221 | 19.4199 | 19.4196 | 19.4195 | 19.4195 |
| 27 | 20.0591 | 19.5154 | 19.4347 | 19.4215 | 19.4194 | 19.4190 | 19.4189 | 19.4189 |
| 28 | 20.0590 | 19.5153 | 19.4347 | 19.4215 | 19.4193 | 19.4189 | 19.4189 | 19.4189 |
| 28.9233 | 20.0590 | 19.5153 | 19.4347 | 19.4215 | 19.4193 | 19.4189 | 19.4189 | 19.4188 |
| 28.9234 | 20.0590 | 19.5153 | 19.4347 | 19.4215 | 19.4193 | 19.4189 | 19.4189 | 19.4188 |
| 28.9235 | 20.0590 | 19.5153 | 19.4347 | 19.4215 | 19.4193 | 19.4189 | 19.4188 | |
| 28.9236 | 20.0590 | 19.5153 | 19.4347 | 19.4215 | 19.4193 | 19.4189 | 19.4188 | 19.4188 |
| 29 | 20.0590 | 19.5153 | 19.4347 | 19.4215 | 19.4193 | 19.4189 | 19.4188 | 19.4188 |
| 30 | 20.0589 | 19.5153 | 19.4346 | 19.4214 | 19.4193 | 19.4189 | 19.4188 | 19.4188 |
"
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 1 | 25.9384 | 25.4230 | 25.3405 | 25.3268 | 25.3246 | 25.3242 | 25.3241 | 25.3241 |
| 5 | 21.1883 | 20.5634 | 20.4691 | 20.4537 | 20.4511 | 20.4507 | 20.4506 | 20.4506 |
| 6 | 20.9145 | 20.3206 | 20.2315 | 20.2169 | 20.2144 | 20.2140 | 20.2140 | 20.2140 |
| 7 | 20.7558 | 20.1900 | 20.1055 | 20.0916 | 20.0893 | 20.0889 | 20.0889 | 20.0889 |
| 8 | 20.6677 | 20.1262 | 20.0456 | 20.0324 | 20.0302 | 20.0298 | 20.0298 | 20.0297 |
| 9 | 20.6229 | 20.1016 | 20.0242 | 20.0115 | 20.0094 | 20.0091 | 20.0090 | 20.0090 |
| 9.3939 | 20.6130 | 20.0987 | 20.0224 | 20.0099 | 20.0079 | 20.0075 | 20.0075 | 20.0074 |
| 9.3940 | 20.6130 | 20.0987 | 20.0224 | 20.0099 | 20.0079 | 20.0075 | 20.0074 | |
| 9.3941 | 20.6130 | 20.0987 | 20.0224 | 20.0099 | 20.0079 | 20.0075 | 20.0074 | 20.0074 |
| 9.3942 | 20.6130 | 20.0987 | 20.0224 | 20.0099 | 20.0079 | 20.0075 | 20.0074 | 20.0074 |
| 9.9 | 20.6050 | 20.0988 | 20.0238 | 20.0116 | 20.0095 | 20.0092 | 20.0091 | 20.0091 |
| 10 | 20.6039 | 20.0993 | 20.0245 | 20.0123 | 20.0102 | 20.0099 | 20.0098 | 20.0098 |
| 11 | 20.6001 | 20.1089 | 20.0362 | 20.0244 | 20.0224 | 20.0221 | 20.0220 | 20.0220 |
| 1 |
Fuhrman S W , Cooper R B . Stochastic decompositions in the M/G/1 queue with generalized vacations. Opns Res, 1985, 33, 1117- 1127
doi: 10.1287/opre.33.5.1117 |
| 2 |
Doshi B T . Queueing systems with vacations: a survey. Queueing Syst, 1986, 1, 29- 66
doi: 10.1007/BF01149327 |
| 3 | 田乃硕. 休假随机服务系统. 北京: 北京大学出版社, 2001 |
| Tian N S . Stochastic Service System with Vacations. Beijing: Peking University Press, 2001 | |
| 4 | 田乃硕. 多级适应性休假的M/G/1 排队. 应用数学, 1992, 5 (4): 12- 18 |
| Tian N S . M/G/1 queue with adaptive multistage vacations. Math Appl, 1992, 5 (4): 12- 18 | |
| 5 |
Zhang Z G , Tian N S . Discrete time Geo/G/1 queue with multiple adaptive vacations. Queueing Syst, 2001, 38 (4): 419- 429
doi: 10.1023/A:1010947911863 |
| 6 | 田乃硕, 徐秀丽, 马占友. 离散时间排队论. 北京: 科学出版社, 2008 |
| Tian N S , Xu X L , Ma Z Y . Discrete-Time Queueing Theory. Beijing: Science Press, 2008 | |
| 7 |
骆川义, 唐应辉, 刘仁彬. 多级适应性休假MX/G/1 排队系统的队长分布. 系统科学与数学, 2007, 27 (6): 899- 907
doi: 10.3969/j.issn.1000-0577.2007.06.011 |
|
Luo C Y , Tang Y H , Liu R B . The queue length distribution of MX/G/1 queueing system with adaptive multistage vacations. J Sys Sci & Math Scis, 2007, 27 (6): 899- 907
doi: 10.3969/j.issn.1000-0577.2007.06.011 |
|
| 8 | 魏瑛源, 唐应辉, 顾建雄. 带有Bernoulli反馈的多级适应性休假的Geo/G/1 排队系统分析. 高校应用数学学报, 2010, 25 (6): 27- 37 |
| Wei Y Y , Tang Y H , Gu J X . Analysis of Geo/G/1 queueing system with multiple adaptive vacations and Bernoulli feedback. Appl Math J Chinese Univ, 2010, 25 (6): 27- 37 | |
| 9 |
Wang T Y , Ke J C , Chang F M . On the discrete-time Geo/G/1 queue with randomized vacations and at most J vacations. Appl Math Model, 2011, 35 (5): 2297- 2308
doi: 10.1016/j.apm.2010.11.021 |
| 10 | Gao S , Wang J T . On a discrete-time GIX/Geo/1/N−G queue with randomized working vacations and at most J vacations. J Ind & Manag Optim, 2015, 11 (3): 779- 806 |
| 11 | Yue D Q , Zhang F . A discrete-time Geo/G/1 retrial queue with J-vacation policy and general retrial times. J Syst Sci & Complex, 2013, 26 (4): 556- 571 |
| 12 | Feyaerts B , Vuyst S D , Bruneel H , et al. The impact of the NT-policy on the behaviour of a discrete-time queue with general service times. J Ind & Manag Optim, 2014, 10 (1): 131- 149 |
| 13 | 唐应辉, 吴文青, 刘云颇. 基于单重休假的Min(N,V) -策略M/G/1 排队系统分析. 应用数学学报, 2014, 37 (6): 976- 996 |
| Tang Y H , Wu W Q , Liu Y P . Analysis of M/G/1 queueing system with Min(N,V)-policy based on single server vacation. Acta Math Appl Sin, 2014, 37 (6): 976- 996 | |
| 14 | 唐应辉, 吴文青, 刘云颇, 等. 基于多重休假的Min(N,V) -策略M/G/1 排队系统的队长分布. 系统工程理论与实践, 2014, 34 (6): 1533- 1546 |
| Tang Y H , Wu W Q , Liu Y P , et al. The queue length distribution of M/G/1 queueing system with Min(N,V) -policy based on multiple server vacations. Syst Eng-Theo & Prac, 2014, 34 (6): 1533- 1546 | |
| 15 | Wu W Q , Tang Y H , Yu M M . Analysis of an M/G/1 queue with multiple vacations, N-policy, unreliable service station and repair facility failures. Int J Sup Oper Manag, 2014, 1 (1): 1- 19 |
| 16 |
Jiang F C , Huang D C , Yang C T , et al. Design strategy for optimizing power consumption of sensor node with Min(N,T) policy M/G/1 queuing model. Int J Com Syst, 2012, 25 (5): 652- 671
doi: 10.1002/dac.1288 |
| 17 | Lan S J , Tang Y H . The structure of departure process and optimal control policy N∗ for Geo/G/1 discrete-time queue with multiple server vacations and Min(N,V)-policy. J Syst Sci & Complex, 2017, 30 (6): 1382- 1402 |
| 18 | 蒋书丽, 唐应辉. 具有多级适应性休假和Min(N,V) -策略控制的M/G/1 排队系统. 系统科学与数学, 2017, 37 (8): 1866- 1884 |
| Jiang S L , Tang Y H . M/G/1 queueing system with multiple adaptive vacations and Min(N,V)-policy. J Sys Sci & Math Scis, 2017, 37 (8): 1866- 1884 | |
| 19 |
Balachandran K R . Control policy for a single server system. Mgmt Sci, 1973, 19, 1013- 1018
doi: 10.1287/mnsc.19.9.1013 |
| 20 | Balachandran K R , Tijms H C . On the D-policy for M/G/1 queue. Mgmt Sci, 1975, 21, 1073- 1076 |
| 21 |
Artalejo J R . On the M/G/1 queue with D-policy. Appl Math Modelling, 2001, 25, 1055- 1069
doi: 10.1016/S0307-904X(01)00031-2 |
| 22 |
Artalejo J R . A note on the optimality of the N- and D-policies for the M/G/1 queue. Oper Res Lett, 2002, 30, 375- 376
doi: 10.1016/S0167-6377(02)00148-7 |
| 23 |
Lee H W , Song K S . Queue length analysis of MAP/G/1 queue under D-policy. Stochastic Models, 2004, 20 (3): 363- 380
doi: 10.1081/STM-200025743 |
| 24 | Lee H W , Baek J W , Jeon J . Analysis of MX/G/1 queue under D-policy. Stochastic Anal & Appl, 2005, 23, 785- 808 |
| 25 |
Lee H W , Seo W J . A mean value formula for the M/G/1 queues controlled by workload. Oper Res Lett, 2007, 35, 472- 476
doi: 10.1016/j.orl.2006.08.001 |
| 26 |
Lee H W , Seo W J . The performance of the M/G/1 queue under the dyadic Min(N,D)-policy and its cost optimization. Perform Eval, 2008, 65, 742- 758
doi: 10.1016/j.peva.2008.04.006 |
| 27 |
Lee H W , Seo W J , Lee S W , et al. Analysis of the MAP/G/1 queue under the Min(N,D)-policy. Stochastic Models, 2010, 26, 98- 123
doi: 10.1080/15326340903517121 |
| 28 | 王敏, 唐应辉. 基于Min(N,D,V) -策略和单重休假的M/G/1 排队系统的最优控制策略. 系统科学与数学, 2018, 38 (9): 1067- 1084 |
| Wang M , Tang Y H . Analysis and optimal policy for M/G/1 queueing system under Min(N,D,V)-policy control. J Sys Sci & Math Scis, 2018, 38 (9): 1067- 1084 | |
| 29 |
Dshalalow J H . Queueing Processes in bulk systems under D-policy. J Appl Probab, 1998, 35, 976- 989
doi: 10.1239/jap/1032438392 |
| 30 | 唐应辉, 唐小我. 排队论-基础与分析技术. 北京: 科学出版社, 2006 |
| Tang Y H , Tang X W . Queueing Theory-Foundations and Analysis Techniques. Beijing: Science Press, 2006 |
| [1] | Zikun Li,Xiuli Xu,Dequan Yue. Analysis of the Fluid Model Driven by M/M/c Queue with Single Working Vacation [J]. Acta mathematica scientia,Series A, 2021, 41(1): 254-268. |
| [2] | Lan Shaojun, Tang Yinghui. Analysis of the Departure Process for Geo/G/1 Discrete-Time Queue with Single Server Vacation and Min-Policy [J]. Acta mathematica scientia,Series A, 2016, 36(2): 380-392. |
|
||