列正交约束下广义Sylvester方程极小化问题的有效算法

Abstract

Abstract:

This paper presents an efficient algorithm for solving the generalized Sylvester equation minimization problem under columnwise orthogonal constraints. Based on some geometric properties of the Stiefel manifold and the MPRP conjugate gradient method in Euclidean space, a Riemannian MPRP conjugate gradient algorithm with Armijo-type line search is proposed to solve the presented problem, and its global convergence is also established. An attractive property of the proposed method is that the direction generated by the method is always a descent direction for the objective function. Some numerical tests are given to show the efficiency of the proposed method. Comparisons with some existing methods are also given.

Key words: Generalized Sylvester equation, Minimization problem, Columnwise orthogonal constraint, Riemannian conjugate gradient method

CLC Number:

O151.1

Yueyuan Liu,Kai Wang,Shujuan Qin,Jiaofen Li. An Effective Algorithm for Generalized Sylvester Equation Minimization Problem Under Columnwise Orthogonal Constraints[J].Acta mathematica scientia,Series A, 2021, 41(2): 479-495.

Trendmd

Figures/Tables 2

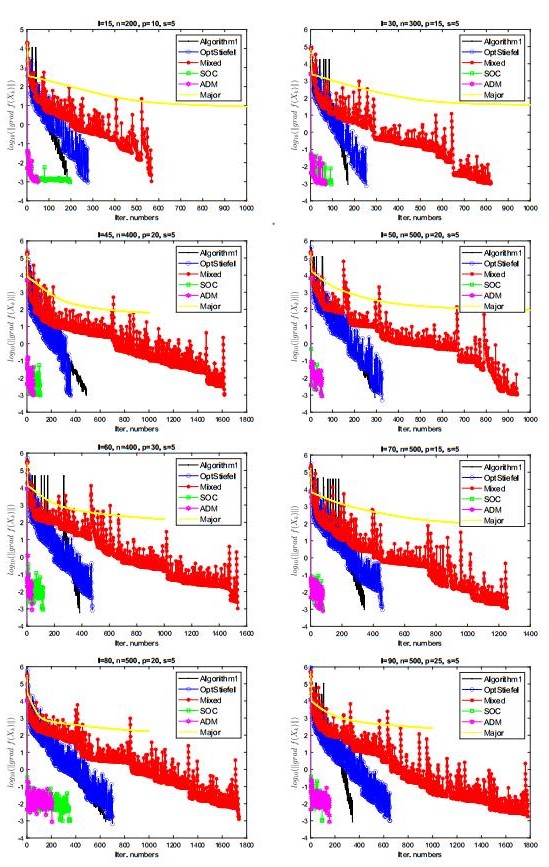
	l, n, p, s	CPU(s)	IT	\|\|grad f(X_k)\|\|	f(X_k)	X_feasi
Algo.1		0.134	183	7.202×10^-4	0	9.744×10^-16
OptStiefel		0.282	246	9.431×10^-4	0	4.220×10^-15
Mixed	15, 200, 10, 5	0.532	568	8.770×10^-4	0	2.048×10^-15
SOC		3.775	196	9.278×10^-4	0	3.593×10^-2
ADM		3.485	49	9.823×10^-4	0	5.866×10^-2
Major		11.784	20000	6.235×10^-2	0.0003	5.209×10^-15
Algo.1		0.205	170	7.973×10^-4	0	1.324×10^-15
OptStiefel		0.904	271	5.123×10^-4	0	1.832×10^-14
Mixed	30, 300, 15, 5	1.524	956	9.914×10^-4	0	2.808×10^-15
SOC		15.229	219	9.536×10^-4	0	3.578×10^-2
ADM		14.663	206	9.741×10^-4	0	3.356×10^-2
Major		32.982	20000	3.500×10^-1	0.0018	6.742×10^-15
Algo.1		0.673	486	5.942×10^-4	0	1.595×10^-15
OptStiefel		1.154	356	5.515×10^-4	0	1.449×10^-15
Mixed	45, 400, 20, 5	4.586	1393	8.224×10^-4	0	4.064×10^-15
SOC		54.639	116	9.679×10^-4	0	5.821×10^-2
ADM		31.334	37	9.979×10^-4	0	1.635×10^-1
Major		114.029	20000	4.797	0.2222	8.883×10^-15
Algo.1		0.647	293	4.311×10^-4	0	1.277×10^-15
OptStiefel		1.216	364	9.407×10^-4	0	1.277×10^-15
Mixed	50, 500, 20, 5	5.546	1156	7.179×10^-4	0	3.165×10^-15
SOC		72.800	51	8.914×10^-4	0	1.201×10^-1
ADM		72.570	46	8.835×10^-4	0	1.313×10^-1
Major		185.344	20000	2.804	0.0429	7.434×10^-15
Algo.1		0.609	239	5.557×10^-1	0.0001	2.313×10^-15
OptStiefel		1.125	398	1.635×10^-2	0	1.524×10^-15
Mixed	60, 400, 30, 5	9.036	2072	1.069×10^-3	0	4.994×10^-15
SOC		88.718	56	9.967×10^-4	0	9.761×10^-2
ADM		105.745	99	9.206×10^-4	0	1.023×10^-1
Major		217.668	20000	1.224×10¹	0.7462	9.998×10^-15
Algo.1		1.866	636	7.307×10^-4	0	1.272×10^-15
OptStiefel		1.846	518	9.739×10^-4	0	8.997×10^-16
Mixed	70, 500, 15, 5	8.198	1966	5.506×10^-4	0	2.639×10^-15
SOC		58.076	97	8.202×10^-4	0	1.162×10^-1
ADM		57.401	83	9.283×10^-4	0	1.065×10^-1
Major		130.671	20000	7.300	0.4279	5.167×10^-15
Algo.1		1.289	645	5.152×10^-4	0	1.798×10^-15
OptStiefel		1.985	669	9.542×10^-4	0	1.287×10^-15
Mixed	80, 500, 20, 5	11.044	2311	8.951×10^-4	0	3.750×10^-15
SOC		126.369	92	8.061×10^-4	0	2.926×10^-1
ADM		186.829	198	8.944×10^-4	0	7.416×10^-2
Major		183.599	20000	1.009×10¹	0.5858	7.192×10^-15

References 28

1	Dehghan M , Hajarian M . An iterative method for solving the generalized coupled Sylvester matrix equations over generalized bisymmetric matrices. Applied Mathematical Modelling, 2010, 34 (3): 639- 654 doi: 10.1016/j.apm.2009.06.018
2	Hajarian M . Developing BiCOR and CORS methods for coupled Sylvester-transpose and periodic Sylvester matrix equations. Applied Mathematical Modelling, 2015, 39 (19): 6073- 6084 doi: 10.1016/j.apm.2015.01.026
3	Hajarian M . Extending the CGLS algorithm for least squares solutions of the generalized Sylvester-transpose matrix equations. Journal of the Franklin Institute, 2016, 353 (5): 1168- 1185 doi: 10.1016/j.jfranklin.2015.05.024
4	Li S K , Huang T Z . LSQR iterative method for generalized coupled Sylvester matrix equations. Applied Mathematical Modelling, 2012, 36 (8): 3545- 3554 doi: 10.1016/j.apm.2011.10.030
5	Ding F , Chen T . On iterative solutions of general coupled matrix equations. SIAM Journal on Control and Optimization, 2006, 44 (6): 2269- 2284 doi: 10.1137/S0363012904441350
6	Bouhamidi A , Jbilou K , Raydan M . Convex constrained optimization for large-scale generalized Sylvester equations. Computational Optimization and Applications, 2011, 48 (2): 233- 253 doi: 10.1007/s10589-009-9253-6
7	Bouhamidi A , Enkhbat R , Jbilou K . Conditional gradient Tikhonov method for a convex optimization problem in image restoration. Journal of Computational and Applied Mathematics, 2014, 255, 580- 592 doi: 10.1016/j.cam.2013.06.011
8	Li J F , Li W , Huang R . An efficient method for solving a matrix least squares problem over a matrix inequality constraint. Computational Optimization and Applications, 2016, 63 (2): 393- 423 doi: 10.1007/s10589-015-9783-z
9	Escalante R , Raydan M . Dykstra's algorithm for a constrained least-squares matrix problem. Numerical Linear Algebra with Applications, 1996, 3 (6): 459- 471 doi: 10.1002/(SICI)1099-1506(199611/12)3:6<459::AID-NLA82>3.0.CO;2-S
10	Escalante R , Raydan M . Dykstra's algorithm for constrained least-squares rectangular matrix problems. Computers & Mathematics with Applications, 1998, 35 (6): 73- 79
11	Monsalve M , Moreno J , Escalante R , Raydan M . Selective alternating projections to find the nearest SDD+ matrix. Applied Mathematics and Computation, 2003, 145 (2/3): 205- 220
12	Li J F , Hu X Y , Zhang L . Dykstra's algorithm for constrained least-squares doubly symmetric matrix problems. Theoretical Computer Science, 2010, 411 (31-33): 2818- 2826 doi: 10.1016/j.tcs.2010.04.011
13	Li J F , Li W , Vong S W , et al. A Riemannian optimization approach for solving the generalized eigenvalue problem for nonsquare matrix pencils. Journal of Scientific Computing, 2020, 82 (3): 1- 43 doi: 10.1007/s10915-020-01173-5
14	Meng C , Hu X , Zhang L . The skew-symmetric orthogonal solutions of the matrix equation AX=B. Linear Algebra and its Applications, 2005, 402, 303- 318 doi: 10.1016/j.laa.2005.01.022
15	Kiers H A . Setting up alternating least squares and iterative majorization algorithms for solving various matrix optimization problems. Computational statistics & data analysis, 2002, 41 (1): 157- 170
16	Kanamori T , Takeda A . Numerical study of learning algorithms on Stiefel manifold. Computational Management Science, 2014, 11 (4): 319- 340 doi: 10.1007/s10287-013-0181-7
17	Lai R , Osher S . A splitting method for orthogonality constrained problems. Journal of Scientific Computing, 2014, 58 (2): 431- 449 doi: 10.1007/s10915-013-9740-x
18	Chen W , Ji H , You Y . An augmented Lagrangian method for 1-regularized optimization problems with orthogonality constraints. SIAM Journal on Scientific Computing, 2016, 38 (4): B570- B592 doi: 10.1137/140988875
19	Sato H , Iwai T . A Riemannian optimization approach to the matrix singular value decomposition. SIAM Journal on Optimization, 2013, 23 (1): 188- 212 doi: 10.1137/120872887
20	Zhu X . A Riemannian conjugate gradient method for optimization on the Stiefel manifold. Computational Optimization and Applications, 2017, 67 (1): 73- 110 doi: 10.1007/s10589-016-9883-4
21	Vandereycken B . Low-rank matrix completion by Riemannian optimization. SIAM Journal on Optimization, 2013, 23 (2): 1214- 1236 doi: 10.1137/110845768
22	Zhao Z , Jin X Q , Bai Z J . A geometric nonlinear conjugate gradient method for stochastic inverse eigenvalue problems. SIAM Journal on Numerical Analysis, 2016, 54 (4): 2015- 2035 doi: 10.1137/140992576
23	Yao T T , Bai Z J , Zhao Z , Ching W K . A Riemannian Fletcher-Reeves conjugate gradient method for doubly stochastic inverse eigenvalue problems. SIAM Journal on Matrix Analysis and Applications, 2016, 37 (1): 215- 234 doi: 10.1137/15M1023051
24	Yao T T , Bai Z J , Zhao Z . A Riemannian variant of the Fletcher-Reeves conjugate gradient method for stochastic inverse eigenvalue problems with partial eigendata. Numerical Linear Algebra with Applications, 2019, 26 (2): e2221 doi: 10.1002/nla.2221
25	Zhang L , Zhou W , Li D H . A descent modified Polak-Ribière-Polyak conjugate gradient method and its global convergence. IMA Journal of Numerical Analysis, 2006, 26 (4): 629- 640 doi: 10.1093/imanum/drl016
26	Absil P A , Mahony R , Sepulchre R . Optimization Aalgorithms on Matrix Manifolds. Princeton: Princeton University Press, 2009
27	Wen Z , Yin W . A feasible method for optimization with orthogonality constraints. Mathematical Programming, 2013, 142 (1/2): 397- 434
28	Oviedo H , Lara H , Dalmau O . A non-monotone linear search algorithm with mixed direction on Stiefel manifold. Optimization Methods and Software, 2019, 34 (2): 437- 457 doi: 10.1080/10556788.2017.1415337

[1]	ZHU Li, XIA Fu-Quan . Levitin-Polyak Well-posedness of Generalized Mixed Variational Inequalities [J]. Acta mathematica scientia,Series A, 2012, 32(4): 633-643.
[2]	YUAN Shi-Fang, LIAO An-Ping, LEI Yuan. Minimization Problem for Hermitian Matrices over the Quaternion Field [J]. Acta mathematica scientia,Series A, 2009, 29(5): 1298-1306.
[3]	Peng Jianwen;Zhu Daoli. Strictly B -Preinvex Functions [J]. Acta mathematica scientia,Series A, 2006, 26(2): 200-206.

An Effective Algorithm for Generalized Sylvester Equation Minimization Problem Under Columnwise Orthogonal Constraints

RichHTML

PDF (PC)

Abstract

Cite this article

share this article

Figures/Tables 2

References 28

Related Articles 3

Metrics

Comments

Recommended 10