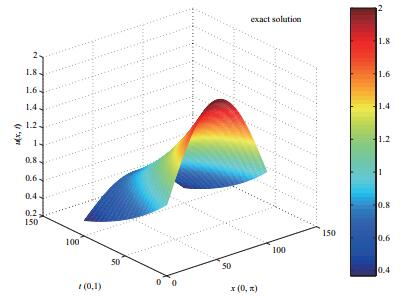
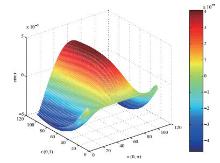
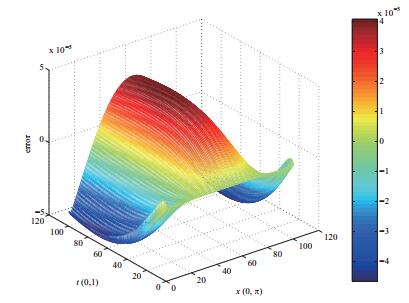
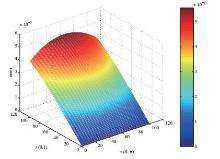
| 1 |
Buchot J M , Raymond J P . The linearized Crocco equation. J Math Fluid Mech, 2006, 8 (4): 510- 541
doi: 10.1007/s00021-005-0186-2
|
| 2 |
Cannarsa P , Martinez P , Vancostenoble J . Null controllability of degenerate heat equations. Adv Differ Equ, 2005, 10, 153- 190
|
| 3 |
Cheng J , Liu J J . A quasi Tikhonov regularization for a two-dimensional backward heat problem by a fundamental solution. Inverse Problems, 2008, 24, 065012
doi: 10.1088/0266-5611/24/6/065012
|
| 4 |
Deng Z C , Qian K , Rao X B , et al. An inverse problem of identifying the source coefficient in a degenerate heat equation. Inverse Probl Sci Eng, 2015, 23, 498- 517
doi: 10.1080/17415977.2014.922079
|
| 5 |
Engl H W , Hanke M , Neubauer A . Regularization of Inverse Problems. Dordrecht: Kluwer Academic Publishers, 1996
|
| 6 |
Johansson T , Lesnic D . Determination of a spacewise dependent heat source. J Comput Appl Math, 2007, 209, 66- 80
doi: 10.1016/j.cam.2006.10.026
|
| 7 |
Johansson T , Lesnic D . A variational method for identifying a spacewise-dependent heat source. IMA J Appl Math, 2007, 72, 748- 760
doi: 10.1093/imamat/hxm024
|
| 8 |
Johansson T , Lesnic D . A procedure for determining a spacewise dependent heat source and the initial temperature. Appl Anal, 2008, 87, 265- 276
doi: 10.1080/00036810701858193
|
| 9 |
Lu J F , Guan Z . Numerical Solution of Partial Differential Equations. Beijing: Tsinghua University Press, 2004
|
| 10 |
Oleinik O A, Radkevič E V. Second Order Differential Equations with Non-Negative Characteristic Form. Providence, RI: American Mathematical Society, 1973
|
| 11 |
Rao X B , Wang Y X , Qian K , et al. Numerical simulation for an inverse source problem in a degenerate parabolic equation. Appl Math Modelling, 2015, 39, 7537- 7553
doi: 10.1016/j.apm.2015.03.016
|
| 12 |
Sun Z Z . Numerical Solution of Partial Differential Equations. Beijing: Science Press, 2005
|
| 13 |
Tort J , Vancostenoble J . Determination of the insolation function in the nonlinear Sellers climate model. Ann I H Poincaré-AN, 2012, 29, 683- 713
doi: 10.1016/j.anihpc.2012.03.003
|
| 14 |
Yang L , Deng Z C , Yu J N , Luo G W . Optimization method for the inverse problem of reconstructing the source term in a parabolic equation. Math Comput Simul, 2009, 80, 314- 326
doi: 10.1016/j.matcom.2009.06.031
|
| 15 |
Yang L , Dehghan M , Yu J N , Luo G W . Inverse problem of time-dependent heat sources numerical reconstruction. Math Comput Simul, 2011, 80, 1656- 1672
|
| 16 |
Yang L , Deng Z C . An inverse backward problem for degenerate parabolic equations. Numer Meth Part Differ Equ, 2017, 33, 1900- 1923
doi: 10.1002/num.22165
|
 ),Zuicha Deng1,2,*(
),Zuicha Deng1,2,*( )
)