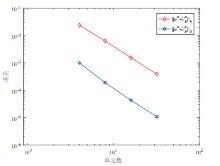
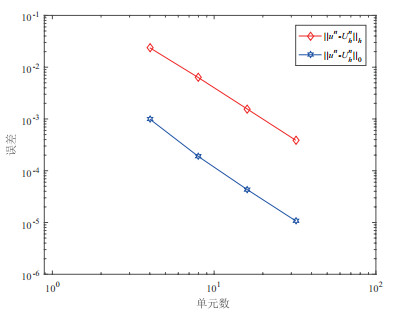
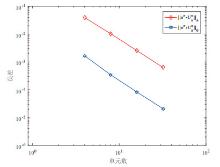
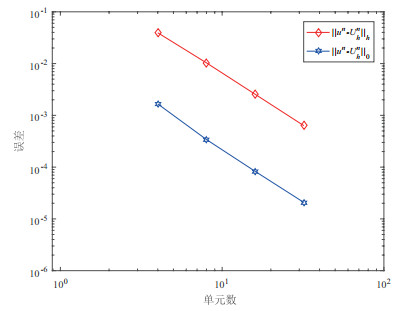
Acta mathematica scientia,Series A ›› 2019, Vol. 39 ›› Issue (5): 1158-1169.
Previous Articles Next Articles
Convergence Analysis of Wilson Element for Parabolic Integro-Differential Equation
Conggang Liang1( ),Xiaoxia Yang1(
),Xiaoxia Yang1( ),Dongyang Shi2(
),Dongyang Shi2( )
)
- 1 School of Mathematics and Statistics, Pingdingshan University, Henan Pingdingshan 467000
2 School of Mathematics and Statistics, Zhengzhou University, Zhengzhou 450001
-
Received:2018-01-30Online:2019-10-26Published:2019-11-08 -
Supported by:the NSFC(11671369);the Science and Technology Planning Foundation of Henan Province(162300410082);the University Cultivation Foundation of Pingdingshan(PXY-PYJJ-2019006)
CLC Number:
- O242.21
Cite this article
Conggang Liang,Xiaoxia Yang,Dongyang Shi. Convergence Analysis of Wilson Element for Parabolic Integro-Differential Equation[J].Acta mathematica scientia,Series A, 2019, 39(5): 1158-1169.
share this article
| 1 | 林群, 严宁宁. 高效有限元构造与分析. 保定: 河北大学出版社, 1996 |
| Lin Q , Yan N N . High Efficient Finite Element Structure and Analysis. Baoding: Hebei University Press, 1996 | |
| 2 |
孟晓然, 石东洋. 抛物积分微分方程非协调类Wilson元的整体超收敛和外推. 数学杂志, 2013, 33 (2): 301- 308
doi: 10.3969/j.issn.0255-7797.2013.02.013 |
|
Meng X R , Shi D Y . Global superconvergence and extrapolation of quasi-wilson element solution to integro-differential of parabolic equations. Journal of Mathematics, 2013, 33 (2): 301- 308
doi: 10.3969/j.issn.0255-7797.2013.02.013 |
|
| 3 |
Chen C , Thomée V , Wahlbin L B . Finite element approximation of a parabolic integro-differential equation with a weakly singular kernel. Mathematics of Computation, 1992, 58 (198): 587- 602
doi: 10.1090/S0025-5718-1992-1122059-2 |
| 4 |
石东洋, 王海红. 抛物型积分微分方程各向异性非协调有限元分析. 工程数学学报, 2009, 26 (2): 209- 218
doi: 10.3969/j.issn.1005-3085.2009.02.003 |
|
Shi D Y , Wang H H . Anisotropic nonconforming finite element analysis for integro-diferential equations of parabolic type. Chinese Journal of Engineering Mathematics, 2009, 26 (2): 209- 218
doi: 10.3969/j.issn.1005-3085.2009.02.003 |
|
| 5 | 孙淑珍, 石翔宇. 抛物型积分微分方程双线性元方法的新估计. 郑州大学学报(理学版), 2016, 48 (4): 6- 9 |
| Sun S Z , Shi X Y . New error estimates of bilinear finite element method to parabolic type integro-differential equation. Journal of Zhengzhou University(Natural Science Edition), 2016, 48 (4): 6- 9 | |
| 6 | 石东洋, 郭城, 王海红. 带弱奇异核的抛物型积分微分方程的非协调有限元方法. 数学物理学报, 2010, 30A (3): 764- 775 |
| Shi D Y , Guo C , Wang H H . Noneonofrming finite element method for integro-diferential equation of parabolie type with weakly singular kernel. Acta Mathematica Scientia, 2010, 30A (3): 764- 775 | |
| 7 |
樊明智, 王芬玲, 牛裕琪, 石东洋. 带弱奇异核非线性积分微分方程的有限元分析. 数学的实践与认识, 2012, 24 (12): 141- 149
doi: 10.3969/j.issn.1000-0984.2012.12.021 |
|
Fan M Z , Wang F L , Niu Y Q , Shi D Y . Finite element analysis of nonlinear integro differential equation with weakly singular kernel. Mathematics in Practice and Theory, 2012, 24 (12): 141- 149
doi: 10.3969/j.issn.1000-0984.2012.12.021 |
|
| 8 | 孙澎涛. 抛物型积分微分方程的非协调Wilson元方法. 数学物理学报, 1996, 16 (S1): 57- 65 |
| Sun P T . Nonconforming wilson element method for parabolic integro differential equations. Acta Mathematica Scientia, 1996, 16 (S1): 57- 65 | |
| 9 |
王芬玲, 石东洋, 陈金环. 非线性抛物积分微分方程的类Wilson非协调元分析. 应用数学, 2012, 25 (4): 923- 935
doi: 10.3969/j.issn.1001-9847.2012.04.032 |
|
Wang F L , Shi D Y , Chen J H . Analysis of quasi-wilson nonconforming element for nonlinear parabolic integro-differential equation. Mathematica Applicata, 2012, 25 (4): 923- 935
doi: 10.3969/j.issn.1001-9847.2012.04.032 |
|
| 10 | 石东洋, 裴丽芳. 非线性抛物型积分微分方程非协调三角形Carey元的收敛性分析. 系统科学与数学, 2009, 29 (6): 854- 864 |
| Shi D Y , Pei L F . Convergence analysis of the nonconforming triangular carey element for a kind of nonlinear parabolic integro-differential problems. Journal of System Science and Mathematical Science, 2009, 29 (6): 854- 864 | |
| 11 |
张铁. 抛物型积分-微分方程有限元近似的超收敛性质. 高等学校计算数学学报, 2001, 23 (3): 193- 201
doi: 10.3969/j.issn.1000-081X.2001.03.001 |
|
Zhang T . Superconvergence of finite element approximations to integro-differential equations of parabolic type. Numerical Mathematics A Journal of Chinese Universities, 2001, 23 (3): 193- 201
doi: 10.3969/j.issn.1000-081X.2001.03.001 |
|
| 12 | Shi D Y , Wang H H . An H1-Galerkin nonconforming mixed finite element method for integro-differential equation of parabolic type. Journal of Mathematical Research and Exposition, 2009, 29 (5): 871- 881 |
| 13 | 赵艳敏, 石东伟, 王芬玲. 抛物型积分微分方程新混合元格式的超逼近分析. 系统科学与数学, 2016, 36 (4): 591- 604 |
| Zhao Y M , Shi D W , Wang F L . Superclose analysis of a new mixed finite element scheme for parabolic intergro-differential equations. Journal of System Science and Mathematical Science, 2016, 36 (4): 591- 604 | |
| 14 |
李秋红, 石东洋. 拟线性抛物型积分微分方程的一个新最低阶混合元格式. 数学的实践与认识, 2012, 42 (23): 272- 275
doi: 10.3969/j.issn.1000-0984.2012.23.037 |
|
Li Q H , Shi D Y . A new lowest order nonconforming mixed finite element formulation for quasi-linear integro-differential equation of parabolic type. Mathematics in Practice and Theory, 2012, 42 (23): 272- 275
doi: 10.3969/j.issn.1000-0984.2012.23.037 |
|
| 15 |
吴志勤, 石东洋. 抛物型积分微分方程的一个新低阶混合元格式. 安徽大学学报(自然科学版), 2012, 36 (6): 1- 4
doi: 10.3969/j.issn.1000-2162.2012.06.001 |
|
Wu Z Q , Shi D Y . A new low order nonconforming mixed finite element formulation for integro-differential equations of parabolic type. Journal of Anhui University(Natural Science Edition), 2012, 36 (6): 1- 4
doi: 10.3969/j.issn.1000-2162.2012.06.001 |
|
| 16 | 刁群, 毛凤梅. 伪抛物型积分微分方程一个新的混合有限元分析. 重庆师范大学学报(自然科学版), 2017, 34 (6): 78- 84 |
| Diao Q , Mao F M . A new mixed finite element analysis for pseudo-parabolic intergo-differential equation. Journal of Chongqing Normal University (Natural Science), 2017, 34 (6): 78- 84 | |
| 17 |
Song S C , Sun M , Jiang L Y . A nonconforming scheme to solve the parabolic problem. Applied Mathematics and Computation, 2015, 265: 108- 119
doi: 10.1016/j.amc.2015.04.089 |
| 18 | 宋士仓, 苏恒迪, 雷蕾. Wilson元求解二阶椭圆问题的一种新格式. 高等学校计算数学学报, 2015, 37 (2): 156- 165 |
| Song S C , Su H D , Lei L . A new scheme of wilson element for second-order elliptic problems. Numerical Mathematics A Journal of Chinese Universities, 2015, 37 (2): 156- 165 | |
| 19 | Douglas J , Dupont T . Interior penalty procedures for elliptic and parabolic galerkin methods. Lecture Notes in Physics, 1976, 58: 207- 216 |
| 20 |
Könnö J , Stenberg R . H(div)-conforming finite elements for the brinkman problem. Mathematical Models and Methods in Applied Sciences, 2011, 21 (11): 2227- 2248
doi: 10.1142/S0218202511005726 |
| [1] | Juan Wang,Jie Zhao. Homogenization of the Neumann Boundary Value Problem: The Sharper W1, p Estimate [J]. Acta mathematica scientia,Series A, 2019, 39(5): 1115-1124. |
| [2] | Zhang Qian, Cai Guanghui. Complete Convergence and Complete Moment Convergence for WOD Random Variables Sequences [J]. Acta mathematica scientia,Series A, 2019, 39(5): 1183-1191. |
| [3] | Yanhua Shi,Yadong Zhang,Fenling Wang,Yanmin Zhao,Pingli Wang. High Accuracy Analysis of Linear Triangular Element for Time Fractional Diffusion Equations [J]. Acta mathematica scientia,Series A, 2019, 39(4): 839-850. |
| [4] | Xiaoling Qiu,Wensheng Jia. An Approximation Theorem of Variational Inequalities Under Bounded Rationality [J]. Acta mathematica scientia,Series A, 2019, 39(4): 730-737. |
| [5] |
Zhihua Zhang,Pingyan Chen.
Complete Convergence for Weighted Sums for  |
| [6] | Dehua Qiu, Juan Xiao. Complete Moment Convergence for Sung's Type Weighted Sums Under END Setup [J]. Acta mathematica scientia,Series A, 2018, 38(6): 1103-1111. |
| [7] | Yadi Zhao, Lifei Wu, Xiaozhong Yang, Shuzhen Sun. A Kind of Efficient Difference Method for the Time Fractional Sub-Diffusion Equation [J]. Acta mathematica scientia,Series A, 2018, 38(6): 1122-1134. |
| [8] | Zhifeng Zhu,Shaoyi Zhang. Study on the Convergence of Nonhomogeneous Markov Chains with Probability Distance [J]. Acta mathematica scientia,Series A, 2018, 38(5): 963-969. |
| [9] | Yang Xuan, Ruan Xiaoe, Wang Peng. Convergence Analysis of Iterative Learning Control for Linear Continuous-Time Switched Systems with Arbitrary Time-Driven Switching Rules [J]. Acta mathematica scientia,Series A, 2018, 38(3): 599-612. |
| [10] | Chen Hongbin, Gan Siqing, Xu Da, Peng Yulong. A Formally Second-Order BDF Compact ADI Difference Scheme for the Two-Dimensional Fractional Evolution Equation [J]. Acta mathematica scientia,Series A, 2017, 37(5): 976-992. |
| [11] | Fu Zongkui, Wu Qunying. A General Result of Precise Asymptotics in Complete Moment Convergence for ρ-mixing Sequence [J]. Acta mathematica scientia,Series A, 2017, 37(3): 544-552. |
| [12] | Qiu Dehua, Duan Zhenghua. Complete Moment Convergence for Weighted Sums of ρ-Mixing Random Variable Sequences [J]. Acta mathematica scientia,Series A, 2017, 37(2): 265-277. |
| [13] | Wang Xuewu. Convergence and Stability of Ishikawa Type Iterative Sequences for the φ-Hemi Pseudocontractive Operator Pair [J]. Acta mathematica scientia,Series A, 2017, 37(2): 248-256. |
| [14] | Cai Gang, Yekini Shehu. Viscosity Iterative Algorithm for Variational Inequality Problems and Fixed Point Problems of Strict Pseudo-Contractions in q-Uniformly Smooth and Uniformly Convex Banach Spaces [J]. Acta mathematica scientia,Series A, 2016, 36(4): 623-638. |
| [15] | Zhang Houchao, Shi Dongyang. Superconvergence Analysis of a Lower Order Mixed Finite Element Method for Nonlinear Fourth-Order Hyperbolic Equation [J]. Acta mathematica scientia,Series A, 2016, 36(4): 656-671. |
| Viewed | ||||||||||||||||||||||||||||||||||||||||||||||
|
Full text 116
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Abstract 86
|
|
|||||||||||||||||||||||||||||||||||||||||||||
Cited |
|
|||||||||||||||||||||||||||||||||||||||||||||
| Shared | ||||||||||||||||||||||||||||||||||||||||||||||
| Discussed | ||||||||||||||||||||||||||||||||||||||||||||||
|