Acta mathematica scientia,Series A ›› 2019, Vol. 39 ›› Issue (5): 1064-1076.
Previous Articles Next Articles
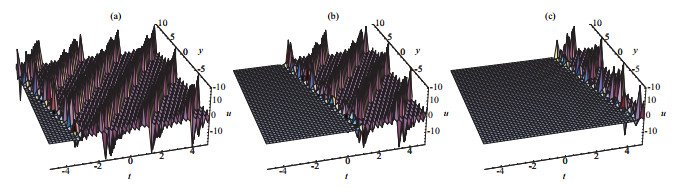
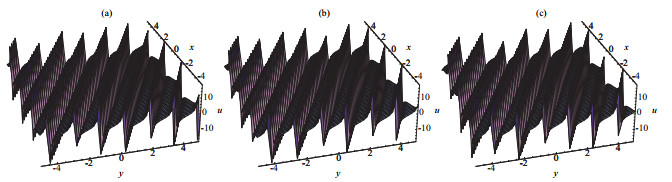
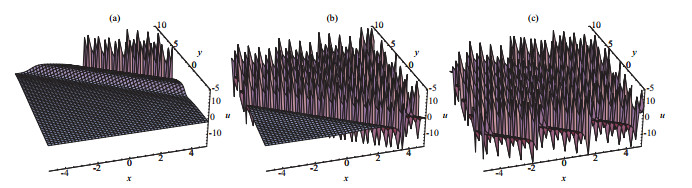
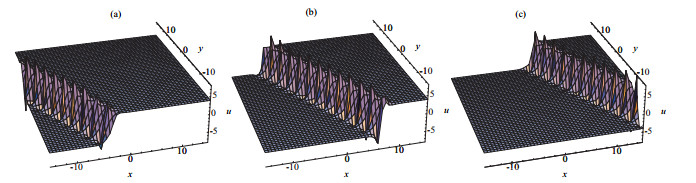
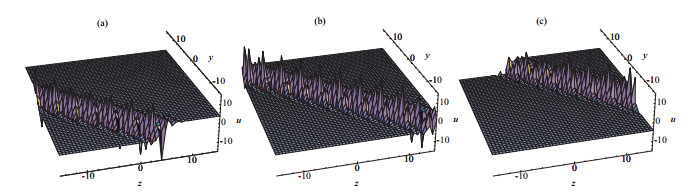
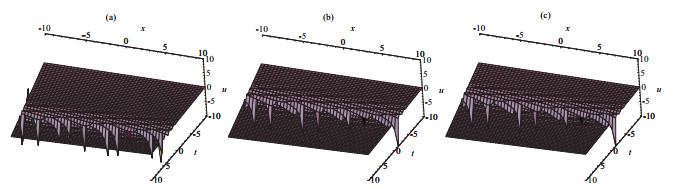
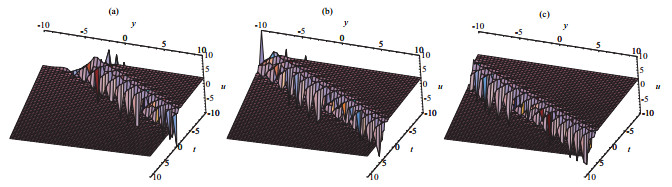
New Exact Periodic Solitary Wave Solutions for the (3+1)-Dimensional Generalized Kadomtsev-Petviashvili Equation
Ying Li1,*( ),Jianguo Liu2,Lianwu Yang1
),Jianguo Liu2,Lianwu Yang1
- 1 School of Mathematical and Computer Science, Yichun University, Jiangxi Yichun 336000
2 College of Computer, Jiangxi University of Traditional Chinese Medicine, Nanchang 330004
-
Received:2018-08-30Online:2019-10-26Published:2019-11-08 -
Contact:Ying Li E-mail:jxsdsxx@bupt.edu.cn -
Supported by:the NSFC(61377067);the Jiangxi Provincial Department of Education(GJJ170889)
CLC Number:
- O175.2
Cite this article
Ying Li,Jianguo Liu,Lianwu Yang. New Exact Periodic Solitary Wave Solutions for the (3+1)-Dimensional Generalized Kadomtsev-Petviashvili Equation[J].Acta mathematica scientia,Series A, 2019, 39(5): 1064-1076.
share this article
| 1 |
Zhou Y , Ma W X . Complexiton solutions to soliton equations by the Hirota method. J Math Phys, 2017, 58 (10): 101511
doi: 10.1063/1.4996358 |
| 2 |
Ma W X , Zhou Y . Reduced D-Kaup-Newell soliton hierarchies from sl(2, R) and so(3, R). Int J Geom Methods M, 2016, 13: 1650105
doi: 10.1142/S021988781650105X |
| 3 |
Yang J Y , Ma W X , Qin Z Y . Lump and lump-soliton solutions to the (2+1)-dimensional Ito equation. Anal Math Phys, 2018, 8: 427- 436
doi: 10.1007/s13324-017-0181-9 |
| 4 |
Ma W X , Qin Z Y , Lü X . Lump solutions to dimensionally reduced p-gKP and p-gBKP equations. Nonlinear Dyn, 2016, 84: 923- 931
doi: 10.1007/s11071-015-2539-6 |
| 5 |
邵光明, 柴晓娟. Navier-Stokes-Fourier方程的可压逼近. 数学物理学报, 2017, 37A (6): 1070- 1084
doi: 10.3969/j.issn.1003-3998.2017.06.007 |
|
Shao G M , Chai X J . Approximation of the incompressible Navier-Stokes-Fourier system by the artificial compressibility method. Acta Math Sci, 2017, 37A (6): 1070- 1084
doi: 10.3969/j.issn.1003-3998.2017.06.007 |
|
| 6 | Ma W X . Complexiton solutions to the Korteweg-de Vries equation. Phys Lett A, 2002, 301 (1): 35- 44 |
| 7 |
Zhang J B , Ma W X . Mixed lump-kink solutions to the BKP equation. Comput Math Appl, 2017, 74: 591- 596
doi: 10.1016/j.camwa.2017.05.010 |
| 8 |
Zhao H Q , Ma W X . Mixed lump-kink solutions to the KP equation. Comput Math Appl, 2017, 74: 1399- 1405
doi: 10.1016/j.camwa.2017.06.034 |
| 9 | 陈林. 一类拟线性Kirchhoff型椭圆方程组多解的存在性. 数学物理学报, 2017, 37A (4): 671- 683 |
| Chen L . Multiple solutions for a quasilinear elliptic system of Kirchhoff type. Acta Math Sci, 2017, 37A (4): 671- 683 | |
| 10 | Ma W X , Yong X , Zhang H Q . Diversity of interaction solutions to the (2+1)-dimensional Ito equation. Comput Math Appl, 2017, 75: 289- 295 |
| 11 | 魏含玉, 夏铁成. 广义Broer-Kaup-Kupershmidt孤子方程的拟周期解. 数学物理学报, 2016, 36A (2): 317- 327 |
| Wei H Y , Xia T C . Quasi-periodic solution of the generalized Broer-Kaup-Kupershmidt soliton equation. Acta Math Sci, 2016, 36A (2): 317- 327 | |
| 12 |
Fan E , Zhang H . A note on the homogeneous balance method. Phys Lett A, 1998, 246: 403- 406
doi: 10.1016/S0375-9601(98)00547-7 |
| 13 |
Fan E . Two new applications of the homogeneous balance method. Phys Lett A, 2000, 265: 353- 357
doi: 10.1016/S0375-9601(00)00010-4 |
| 14 | Senthilvelan M . On the extended applications of homogeneous balance method. Appl Math Comput, 2001, 123: 381- 388 |
| 15 |
Zhang S . The periodic wave solutions for the (2+1) dimensional Konopelchenko-Dubrovsky equations. Chaos Soliton Fract, 2006, 30: 1213- 1220
doi: 10.1016/j.chaos.2005.08.201 |
| 16 |
El-Sabbagh M F , Ali A T . Nonclassical symmetries for nonlinear partial differential equations via compatibility. Commun Theor Phys, 2011, 56: 611- 616
doi: 10.1088/0253-6102/56/4/02 |
| 17 |
Liu J G , Zhou L , He Y . Multiple soliton solutions for the new (2+1)-dimensional Korteweg-de Vries equation by multiple exp-function method. Appl Math Lett, 2018, 80: 71- 78
doi: 10.1016/j.aml.2018.01.010 |
| 18 | El-Sabbagh M F , Ali A T , El-Ganaini S . New abundant exact solutions for the system of (2+1)-dimensional Burgers equations. Appl Math Inform Sci, 2008, 2 (1): 31- 41 |
| 19 |
Dai C Q , Wang Y Y , Zhang J F . Analytical spatiotemporal localizations for the generalized (3+1)-dimensional nonlinear Schrödinger equation. Opt Lett, 2010, 35: 1437- 1439
doi: 10.1364/OL.35.001437 |
| 20 |
Zhang S . A generalized auxiliary equation method and its application to (2+1)-dimensional Korteweg-de Vries equations. Comput Math Appl, 2007, 54: 1028- 1038
doi: 10.1016/j.camwa.2006.12.046 |
| 21 |
Wu G C , Xia T C . Uniformly constructing exact discrete soliton solutions and periodic solutions to differential-difference equations. Comput Math Appl, 2009, 58: 2351- 2354
doi: 10.1016/j.camwa.2009.03.022 |
| 22 |
Wang C J , Dai Z D , Mu G , Lin S Q . New exact periodic solitary-wave solutions for new (2+1)-dimensional KdV equation. Commun Theor Phys, 2009, 52: 862- 864
doi: 10.1088/0253-6102/52/5/21 |
| 23 | Dai Z D , Lin S Q , Fu H M , Zeng X P . Exact three-wave solutions for the KP equation. Appl Math Comput, 2010, 216 (5): 1599- 1604 |
| 24 |
Zeng X P , Dai Z D , Li D L . New periodic soliton solutions for the (3+1)-dimensional potential-YTSF equation. Chaos Soliton Fract, 2009, 42: 657- 661
doi: 10.1016/j.chaos.2009.01.040 |
| 25 |
Dai Z D , Li S L , Dai Q Y , Huang J . Singular periodic soliton solutions and resonance for the KadomtsevPetviashvili equation. Chaos Soliton Fract, 2007, 34 (4): 1148- 1153
doi: 10.1016/j.chaos.2006.04.028 |
| 26 | Dai Z D , Liu Z J , Li D L . Exact periodic solitary-wave solution for KdV equation. Chin Phys Lett, 2008, 25 (5): 1151- 1153 |
| 27 | Ablowitz M J , Clarkson P A . Solitons, Nonlinear Evolution Equations and Inverse Scattering Transform. Cambridge: Cambridge University Press, 1990 |
| 28 |
Manukure S , Zhou Y , Ma W X . Lump solutions to a (2+1)-dimensional extended KP equation. Comput Math Appl, 2018, 75 (7): 2414- 2419
doi: 10.1016/j.camwa.2017.12.030 |
| 29 |
Ma W X . Lumps and their interaction solutions of (3+1)-dimensional linear PDEs. J Geom Phys, 2018, 133: 10- 16
doi: 10.1016/j.geomphys.2018.07.003 |
| 30 |
Ma W X , Zhou Y . Lump solutions to nonlinear partial differential equations via Hirota bilinear forms. J Differential Equations, 2018, 264: 2633- 2659
doi: 10.1016/j.jde.2017.10.033 |
| 31 |
Chen S T , Ma W X . Lump solutions to a generalized Bogoyavlensky-Konopelchenko equation. Front Math China, 2018, 13 (3): 525- 534
doi: 10.1007/s11464-018-0694-z |
| 32 | Ma W X , Zhu Z . Solving the (3+1)-dimensional generalized KP and BKP equations by the multiple exp-function algorithm. Appl Math Comput, 2012, 218 (24): 11871- 11879 |
| 33 | Xia T C , Li B , Zhang H Q . New explicit and exact solutions for the Nizhnik-Novikov-Vesselov equationy. Appl Math E-Notes, 2001, 1: 139- 142 |
| 34 |
Tang Y N , Zai W J . New exact periodic solitary-wave solutions for the (3+1)-dimensional generalized KP and BKP equations. Comput Math Appl, 2015, 70 (10): 2432- 2441
doi: 10.1016/j.camwa.2015.09.017 |
| 35 |
Ma W X , Fan E G . Linear superposition principle applying to Hirota bilinear equations. Comput Math Appl, 2011, 61: 950- 959
doi: 10.1016/j.camwa.2010.12.043 |
| 36 |
Ma W X , Abdeljabbar A . A bilinear bäcklund transformation of a (3+1)-dimensional generalized KP equation. Appl Math Lett, 2012, 25 (10): 1500- 1504
doi: 10.1016/j.aml.2012.01.003 |
| 37 |
Peng W Q , Tian S F , Zhang T T . Analysis on lump, lumpoff and rogue waves with predictability to the (2+1)-dimensional B-type Kadomtsev-Petviashvili equation. Phys Lett A, 2018, 382 (38): 2701- 2708
doi: 10.1016/j.physleta.2018.08.002 |
| 38 |
Qin C Y , Tian S F , Wang X B , et al. Rogue waves, bright-dark solitons and traveling wave solutions of the (3+1)-dimensional generalized Kadomtsev-Petviashvili equation. Comput Math Appl, 2018, 75 (12): 4221- 4231
doi: 10.1016/j.camwa.2018.03.024 |
| 39 |
Tu J M , Tian S F , Xu M J , et al. Bäcklund transformation, rogue wave solutions and interaction phenomena for a (3+1)-dimensional B-type Kadomtsev-Petviashvili-Boussinesq equation. Nonlinear Dyn, 2018, 92 (2): 709- 720
doi: 10.1007/s11071-018-4085-5 |
| 40 |
Wang X B , Tian S F , Qin C Y , Zhang T T . Characteristics of the solitary waves and rogue waves with interaction phenomena in a generalized (3+1)-dimensional Kadomtsev-Petviashvili equation. Appl Math Lett, 2017, 72: 58- 64
doi: 10.1016/j.aml.2017.04.009 |
| 41 |
Wang X B , Tian S F , Yan H , Zhang T T . On the solitary waves, breather waves and rogue waves to a generalized (3+1)-dimensional Kadomtsev-Petviashvili equation. Comput Math Appl, 2017, 74 (3): 556- 563
doi: 10.1016/j.camwa.2017.04.034 |
| 42 |
Tu J M , Tian S F , Xu M J , Ma P L . waves, solitary waves and asymptotic properties for a generalized (3+1)-dimensional variable-coefficient B-type Kadomtsev-Petviashvili equation. Nonlinear Dyn, 2017, 88 (3): 2265- 2279
doi: 10.1007/s11071-017-3375-7 |
| 43 |
Feng L L , Tian S F , Wang X B , Zhang T T . Rogue waves, homoclinic breather waves and soliton waves for the (2+1)-dimensional B-type Kadomtsev-Petviashvili equation. Appl Math Lett, 2017, 65: 90- 97
doi: 10.1016/j.aml.2016.10.009 |
| 44 |
Tu J M , Tian S F , Xu M J , et al. On periodic wave solutions with asymptotic behaviors to a (3+1)-dimensional generalized B-type Kadomtsev-Petviashvili equation in fluid dynamics. Comput Math Appl, 2016, 72 (9): 2486- 2504
doi: 10.1016/j.camwa.2016.09.003 |
| 45 |
Tian S F , Zhang H Q . On the integrability of a generalized variable-coefficient Kadomtsev-Petviashvili equation. J Phys A:Math Theor, 2012, 45 (5): 055203
doi: 10.1088/1751-8113/45/5/055203 |
| 46 |
Wang X B , Tian S F , Feng L L , Zhang T T . On quasi-periodic waves and rogue waves to the (4+1)-dimensional nonlinear Fokas equation. J Math Phys, 2018, 59 (7): 073505
doi: 10.1063/1.5046691 |
| 47 | Wang X B , Tian S F , Xu M J , Zhang T T . On integrability and quasi-periodic wave solutions to a (3+1)-dimensional generalized KdV-like model equation. Appl Math Comput, 2016, 283: 216- 233 |
| 48 |
Tu J M , Tian S F , Xu M J , et al. Bäcklund transformation, infinite conservation laws and periodic wave solutions of a generalized (3+1)-dimensional nonlinear wave in liquid with gas bubbles. Nonlinear Dyn, 2016, 83 (3): 1199- 1215
doi: 10.1007/s11071-015-2397-2 |
| 49 |
Xu M J , Tian S F , Tu J M , Zhang T T . Bäcklund transformation, infinite conservation laws and periodic wave solutions to a generalized (2+1)-dimensional Boussinesq equation. Nonlinear Anal-Real, 2016, 31: 388- 408
doi: 10.1016/j.nonrwa.2016.01.019 |
| 50 |
Tu J M , Tian S F , Xu M J , Zhang T T . Quasi-periodic waves and solitary waves to a generalized KdVCaudrey-Dodd-Gibbon equation from fluid dynamics. Taiwanese J Math, 2016, 20 (4): 823- 848
doi: 10.11650/tjm.20.2016.6850 |
| 51 | Xu M J , Tian S F , Tu J M , et al. On quasiperiodic wave solutions and integrability to a generalized (2+1)-dimensional Korteweg-de Vries equation. Nonlinear Dyn, 2016, 82 (4): 2031- 2049 |
| 52 |
Tian S F , Zhang H Q . On the integrability of a generalized variable-coefficient forced Korteweg-de Vries equation in fluids. Stud Appl Math, 2014, 132 (3): 212- 246
doi: 10.1111/sapm.12026 |
| [1] | Jimeng Li. Oscillation Analysis of Second-Order Generalized Emden-Fowler-Type Delay Differential Equations [J]. Acta mathematica scientia,Series A, 2019, 39(5): 1041-1054. |
| [2] | Siqian Qin,Zhengqiu Ling,Zewen Zhou. Some Methods for Determining the Lower Bound of Blow-up Time in a Parabolic Problem and Effectiveness Analysis [J]. Acta mathematica scientia,Series A, 2019, 39(5): 1033-1040. |
| [3] | Liu Shujun. Weak Solutions for the Systems of Multifluid Flows [J]. Acta mathematica scientia,Series A, 2019, 39(5): 1077-1086. |
| [4] | Mei Yanfang, Wang Youjun. Three Types of Solutions for a Class of Nonlinear Schrödinger Equations [J]. Acta mathematica scientia,Series A, 2019, 39(5): 1087-1093. |
| [5] | Wu Jie, Lin Hongxia. The Global Solution and Asymptotic Behavior of Parabolic-Parabolic Keller-Segel Type Model [J]. Acta mathematica scientia,Series A, 2019, 39(5): 1102-1114. |
| [6] | Wang Juan, Zhao Jie. Homogenization of the Neumann Boundary Value Problem: The Sharper W1,p Estimate [J]. Acta mathematica scientia,Series A, 2019, 39(5): 1115-1124. |
| [7] | Zhang Qiuyue. Global Regularity for 3D Generalized Oldroyd-B Type Models with Fractional Dissipation [J]. Acta mathematica scientia,Series A, 2019, 39(5): 1125-1135. |
| [8] | Zhang Ruifeng, Liu Nan. Gradient Flow Method in Nonlinear Optical Lattices [J]. Acta mathematica scientia,Series A, 2019, 39(5): 1170-1182. |
| [9] | Yafeng Li,Qiao Xin,Chunlai Mu. The Discrete Possion Equation and the Heat Equation with the Exponential Nonlinear Term [J]. Acta mathematica scientia,Series A, 2019, 39(4): 773-784. |
| [10] | Na Wang,Shu Wang. The Boundary Layer for MHD Equations in a Plane-Parallel Channel [J]. Acta mathematica scientia,Series A, 2019, 39(4): 738-760. |
| [11] | Hailong Yuan,Yuping Wang,Yanling Li. Positive Solutions of a Predator-Prey Model with Cross Diffusion [J]. Acta mathematica scientia,Series A, 2019, 39(3): 545-559. |
| [12] |
Xiaohang Ou.
Sufficient and Necessary Condition for the Existence of Positive Entire Solutions of a Nonlinear Biharmonic Equations on  |
| [13] | Kai Li,Han Yang,Fan Wang. Study on Weak Solution and Strong Solution of Incompressible MHD Equations with Damping in Three-Dimensional Systems [J]. Acta mathematica scientia,Series A, 2019, 39(3): 518-528. |
| [14] | Xue Zhang,Yuhuai Sun. Dynamical Analysis and Traveling Wave Solutions for Generalized (3+1)-Dimensional Kadomtsev-Petviashvili Equation [J]. Acta mathematica scientia,Series A, 2019, 39(3): 501-509. |
| [15] | Changqing Tong,Jing Zheng. Periodic Solutions of a Semi-Linear Klein-Gordon Equations with High Frequencies [J]. Acta mathematica scientia,Series A, 2019, 39(3): 484-500. |
| Viewed | ||||||||||||||||||||||||||||||||||||||||||||||
|
Full text 143
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Abstract 123
|
|
|||||||||||||||||||||||||||||||||||||||||||||
Cited |
|
|||||||||||||||||||||||||||||||||||||||||||||
| Shared | ||||||||||||||||||||||||||||||||||||||||||||||
| Discussed | ||||||||||||||||||||||||||||||||||||||||||||||
|