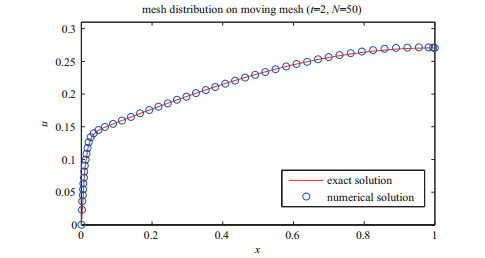
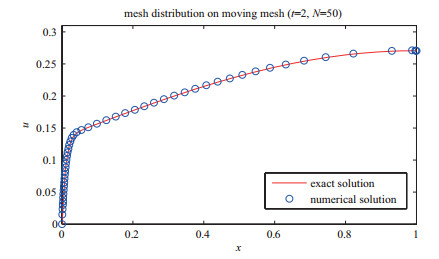
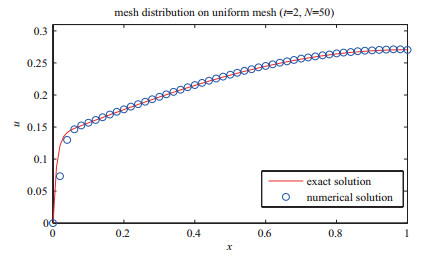
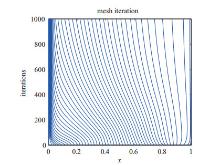
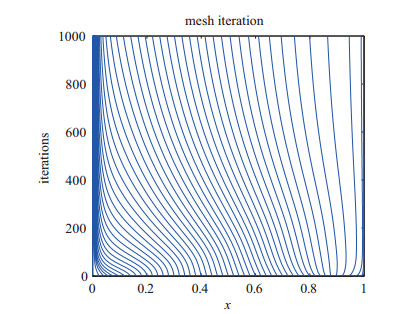
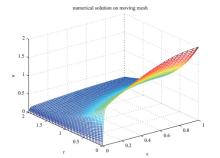
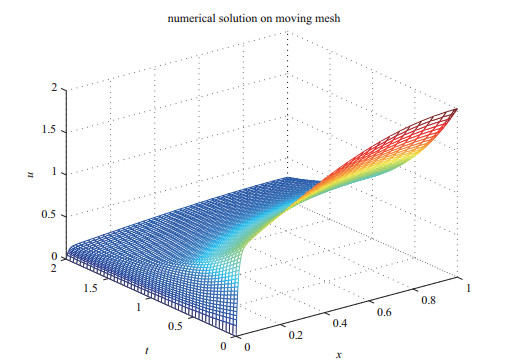
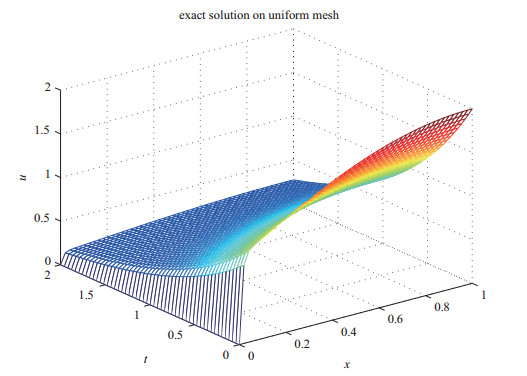
Acta mathematica scientia,Series A ›› 2019, Vol. 39 ›› Issue (4): 942-950.
Previous Articles Next Articles
Adaptive Mesh Method for Solving a Second-Order Hyperbolic Equation
- 1 School of Information Mechanical and Electrical Engineering, Hunan International Economics University, Changsha 410205
2 Hunan Key Laboratory for Computation and Simulation in Science and Engineering, Xiangtan University, Hunan Xiangtan 411105
-
Received:2018-04-02Online:2019-08-26Published:2019-09-11 -
Contact:Qin Zhou E-mail:19891881@qq.com -
Supported by:the NSFC(11671342);the Scientific Research Fund of Hunan Provincial Education Department(18C1097);the Natural Science Foundation of Hunan Province(2018JJ2374)
CLC Number:
- O241.82
Cite this article
Qin Zhou,Yin Yang. Adaptive Mesh Method for Solving a Second-Order Hyperbolic Equation[J].Acta mathematica scientia,Series A, 2019, 39(4): 942-950.
share this article
| 1 | 张文生. 科学计算中的偏微分方程有限差分法. 北京: 高等教育出版社, 2006 |
| Zhang W S . Finite Difference Method for Partial Differential Equations in Scientific Computing. Beijing: Higher Education Press, 2006 | |
| 2 |
程晓晗, 聂玉峰, 蔡力, 封建湖. 基于移动网格的熵稳定格式. 计算物理, 2017, 34 (2): 175- 182
doi: 10.3969/j.issn.1001-246X.2017.02.007 |
|
Cheng X , Nie Y , Cai L , Feng J H . Entropy stable scheme based on moving meshes for hyperbolic conservation laws. Chinese Journal of Computational Physics, 2017, 34 (2): 175- 182
doi: 10.3969/j.issn.1001-246X.2017.02.007 |
|
| 3 |
Tan Z J , Zhang Z , Huang Y Q , Tang T . Moving mesh methods with locally varying time steps. J Comput Phys, 2004, 200: 347- 367
doi: 10.1016/j.jcp.2004.04.007 |
| 4 |
Tang H Z , Tang T . Adaptive mesh methods for one-and two-dimensional hyperbolic conservation laws. SIAM Journal on Numerical Analysis, 2003, 41 (2): 487- 515
doi: 10.1137/S003614290138437X |
| 5 | 陈艳萍, 刘利斌. 一类奇异摄动对流扩散方程组的自适应移动网格方法. 华南师范大学学报(自然科学版), 2013, 45 (6): 1- 5 |
| Chen Y , Liu L B . An adaptive moving grid method for the singularly perturbed convection-diffusion problem. Journal of South China Normal University (Natural Science Edition), 2013, 45 (6): 1- 5 | |
| 6 |
Zhou Q , Chen Y , Yang Y . Two improved algorithms and implementation for a singularly perturbed problem on moving meshes. Journal of Systems Science and Complexity, 2011, 24 (6): 1232- 1240
doi: 10.1007/s11424-011-8138-9 |
| 7 |
Abdulghani A , Naire S . An adaptive moving mesh method for thin film flow equations with surface tension. Journal of Computational and Applied Mathematics, 2017, 319: 365- 384
doi: 10.1016/j.cam.2017.01.019 |
| 8 |
Zhang Z R , Tang T . An adaptive mesh redistribution algorithm for convection-dominated problems. Commun Pure Appl Anal, 2002, 1: 341- 357
doi: 10.3934/cpaa.2002.1.341 |
| 9 | Ngo C , Huang W . A Study on Moving Mesh Finite Element Solution of the Porous Medium Equation. Journal of Computational Physics, 2016, 331: 357- 380 |
| 10 |
Hu G , Qiao Z , Tang T . Moving Finite Element Simulations for Reaction-Diffusion Systems. Advances in Applied Mathematics Mechanics, 2012, 4 (3): 365- 381
doi: 10.4208/aamm.10-m11180 |
| 11 | Zhang Z , Qiao Z . The adaptive time step method for solving phase field crystal model. Journal of Computational Physics, 2013, 249 (3): 204- 215 |
| 12 |
Zhang Z , Qiao Z . An adaptive time-stepping strategy for the Cahn-Hilliard equation. Commun Comput Phys, 2012, 11 (4): 1261- 1278
doi: 10.4208/cicp.300810.140411s |
| 13 |
Qiao Z , Zhang Z , Tang T . An adaptive time-stepping strategy for the molecular beam epitaxy models. SIAM J Sci Comput, 2011, 33 (3): 1395- 1414
doi: 10.1137/100812781 |
| [1] | Yadi Zhao, Lifei Wu, Xiaozhong Yang, Shuzhen Sun. A Kind of Efficient Difference Method for the Time Fractional Sub-Diffusion Equation [J]. Acta mathematica scientia,Series A, 2018, 38(6): 1122-1134. |
| [2] | Chen Hongbin, Gan Siqing, Xu Da, Peng Yulong. A Formally Second-Order BDF Compact ADI Difference Scheme for the Two-Dimensional Fractional Evolution Equation [J]. Acta mathematica scientia,Series A, 2017, 37(5): 976-992. |
| [3] | Zhang Houchao, Shi Dongyang. Superconvergence Analysis of a Lower Order Mixed Finite Element Method for Nonlinear Fourth-Order Hyperbolic Equation [J]. Acta mathematica scientia,Series A, 2016, 36(4): 656-671. |
| [4] | LUO Zhen-Dong, LI Hong. A POD REDUCED-ORDER SPDMFE EXTRAPOLATING ALGORITHM FOR HYPERBOLIC EQUATIONS [J]. Acta mathematica scientia,Series A, 2014, 34(3): 872-890. |
| [5] | FANG Zhi-Chao, LI Hong, LUO Zhen-Dong. A Mixed Covolume Method for Pseudo-Hyperbolic Equation [J]. Acta mathematica scientia,Series A, 2013, 33(3): 535-550. |
| [6] | YANG Yin, ZHOU Qin. Crank-Nicolson Difference Scheme for Convection-Diffusion Problem by Using |Moving Mesh Method [J]. Acta mathematica scientia,Series A, 2011, 31(4): 1063-1070. |
| [7] | AN Jing, LUO Zhen-Dong. A Reduced Finite Difference Scheme Based on POD Bases and Posteriori Error Estimation for the Three Parabolic Equation [J]. Acta mathematica scientia,Series A, 2011, 31(3): 769-775. |
| [8] | YUAN Hong-Jun, TONG Li-Ning. BV Solutions for the Quasilinear Hyperbolic Equation with Nonlinear Source and Finite Radon Measure as Initial Conditions [J]. Acta mathematica scientia,Series A, 2010, 30(1): 54-70. |
| [9] | KONG Ling-Hai, HUAN Zhong-Dan. A Forward and Backward Diffusion Model for Gray Level Image Restoration [J]. Acta mathematica scientia,Series A, 2009, 29(6): 1771-1784. |
| [10] | Chen Juan; Zhang Luming. Numerical Approximation of Solution for the Initial-boundary Value Problem of the Klein-Gordon-Zakharov Equations [J]. Acta mathematica scientia,Series A, 2009, 29(2): 494-504. |
| [11] | Wang Yanping; Guo Boling. Blow-up of Solution for an Initial Boundary Value Problem for a Nonlinear Hyperbolic Equation [J]. Acta mathematica scientia,Series A, 2008, 28(4): 688-693. |
| [12] | Zhang Jing;Zhang Luming;Chen Juan. A Numerical Simulation Method of Nonlinear Schrodinger equation [J]. Acta mathematica scientia,Series A, 2007, 27(6): 1111-1117. |
| [13] | Wang Tingchun; Zhang Luming. Pseudo-Compact Conservative Finite Difference Approximate Solution for the Symmetric Regularized-Long-Wave Equation [J]. Acta mathematica scientia,Series A, 2006, 26(6): 1039-. |
| [14] | ZHANG Quan-Ju. The Cauchy Problems of a class of Equations |for the Tension of Extensible Beam [J]. Acta mathematica scientia,Series A, 2003, 23(6): 704-710. |
| Viewed | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
Full text 140
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Abstract 85
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
Cited |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
| Shared | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Discussed | ||||||||||||||||||||||||||||||||||||||||||||||||||
|