In this article, we consider the drift parameter estimation problem for the nonergodic Ornstein-Uhlenbeck process defined as d
Xt=
θXtd
t + d
Gt,
t ≥ 0 with an unknown parameter
θ > 0, where G is a Gaussian process. We assume that the process {
Xt,
t ≥ 0} is observed at discrete time instants
t1=△
n,…,
tn=
n△
n, and we construct two least squares type estimators
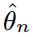
and
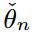
for
θ on the basis of the discrete observations {
Xti,
i=1,…,
n} as
n → ∞. Then, we provide sufficient conditions, based on properties of G, which ensure that
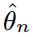
and
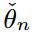
are strongly consistent and the sequences √
n△n(
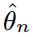
-
θ) and √
n△n(
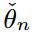
-
θ) are tight. Our approach offers an elementary proof of[11], which studied the case when
G is a fractional Brownian motion with Hurst parameter
H ∈ (1/2, 1). As such, our results extend the recent findings by[11] to the case of general Hurst parameter
H ∈ (0, 1). We also apply our approach to study subfractional Ornstein-Uhlenbeck and bifractional Ornstein-Uhlenbeck processes.