Table of Content

25 October 2018, Volume 38 Issue 5 Previous Issue    Next Issue

For Selected:

View Abstracts

Download Citations EndNote Reference Manager ProCite BibTeX RefWorks

Toggle Thumbnails

Articles

Select

Preface Gui-Qiang Chen, Banghe Li and Xiping Zhu Acta Mathematica Scientia. 2018, 38 (5):  1441-1442.  Abstract ( 56 )   RICH HTML PDF (59KB) ( 70 )   Save Related Articles | Metrics

Select

REGULARIZATION OF PLANAR VORTICES FOR THE INCOMPRESSIBLE FLOW Daomin CAO, Shuangjie PENG, Shuangjie PENG Acta Mathematica Scientia. 2018, 38 (5):  1443-1467.  Abstract ( 92 )   RICH HTML PDF   Save In this paper, we continue to construct stationary classical solutions for the incompressible planar flows approximating singular stationary solutions of this problem. 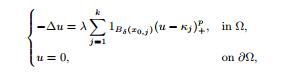This procedure is carried out by constructing solutions for the following elliptic equations where 0 < p < 1, Ω ? R2 is a bounded simply-connected smooth domain, κi (i=1, …, k) is prescribed positive constant. The result we prove is that for any given non-degenerate critical point x0=(x0,1, …, x0,k) of the Kirchhoff-Routh function defined on Ωk corresponding to (κ1, …, κk), there exists a stationary classical solution approximating stationary k points vortex solution. Moreover, as λ → +∞, the vorticity set {y:uλ > κj} ∩ Bδ(x0,j) shrinks to {x0,j}, and the local vorticity strength near each x0,j approaches κj, j=1, …, k. This result makes the study of the above problem with p ≥ 0 complete since the cases p > 1, p=1, p=0 have already been studied in [11, 12] and [13] respectively. References | Related Articles | Metrics

Select

YAU'S UNIFORMIZATION CONJECTURE FOR MANIFOLDS WITH NON-MAXIMAL VOLUME GROWTH Binglong CHEN, Xiping ZHU Acta Mathematica Scientia. 2018, 38 (5):  1468-1484.  Abstract ( 92 )   RICH HTML PDF   Save The well-known Yau's uniformization conjecture states that any complete noncompact Kähler manifold with positive bisectional curvature is bi-holomorphic to the Euclidean space. The conjecture for the case of maximal volume growth has been recently confirmed by G. Liu in [23]. In the first part, we will give a survey on the progress. In the second part, we will consider Yau's conjecture for manifolds with non-maximal volume growth. We will show that the finiteness of the first Chern number C1n is an essential condition to solve Yau's conjecture by using algebraic embedding method. Moreover, we prove that, under bounded curvature conditions, C1n is automatically finite provided that there exists a positive line bundle with finite Chern number. In particular, we obtain a partial answer to Yau's uniformization conjecture on Kähler manifolds with minimal volume growth. References | Related Articles | Metrics

Select

STABILITY OF STEADY MULTI-WAVE CONFIGURATIONS FOR THE FULL EULER EQUATIONS OF COMPRESSIBLE FLUID FLOW Gui-Qiang G. CHEN, Matthew RIGBY Acta Mathematica Scientia. 2018, 38 (5):  1485-1514.  Abstract ( 44 )   RICH HTML PDF   Save We are concerned with the stability of steady multi-wave configurations for the full Euler equations of compressible fluid flow. In this paper, we focus on the stability of steady four-wave configurations that are the solutions of the Riemann problem in the flow direction, consisting of two shocks, one vortex sheet, and one entropy wave, which is one of the core multi-wave configurations for the two-dimensional Euler equations. It is proved that such steady four-wave configurations in supersonic flow are stable in structure globally, even under the BV perturbation of the incoming flow in the flow direction. In order to achieve this, we first formulate the problem as the Cauchy problem (initial value problem) in the flow direction, and then develop a modified Glimm difference scheme and identify a Glimm-type functional to obtain the required BV estimates by tracing the interactions not only between the strong shocks and weak waves, but also between the strong vortex sheet/entropy wave and weak waves. The key feature of the Euler equations is that the reflection coefficient is always less than 1, when a weak wave of different family interacts with the strong vortex sheet/entropy wave or the shock wave, which is crucial to guarantee that the Glimm functional is decreasing. Then these estimates are employed to establish the convergence of the approximate solutions to a global entropy solution, close to the background solution of steady four-wave configuration. References | Related Articles | Metrics

Select

ONE-DIMENSIONAL VISCOUS RADIATIVE GAS WITH TEMPERATURE DEPENDENT VISCOSITY Lin HE, Yongkai LIAO, Tao WANG, Huijiang ZHAO Acta Mathematica Scientia. 2018, 38 (5):  1515-1548.  Abstract ( 49 )   RICH HTML PDF   Save This paper is concerned with the construction of global, large amplitude solutions to the Cauchy problem of the one-dimensional compressible Navier-Stokes system for a viscous radiative gas when the viscosity and heat conductivity coefficients depend on both specific volume and absolute temperature. The data are assumed to be without vacuum, mass concentrations, or vanishing temperatures, and the same is shown to be hold for the global solution constructed. The proof is based on some detailed analysis on uniform positive lower and upper bounds of the specific volume and absolute temperature. References | Related Articles | Metrics

Select

MACROSCOPIC REGULARITY FOR THE BOLTZMANN EQUATION Feimin HUANG, Yong WANG Acta Mathematica Scientia. 2018, 38 (5):  1549-1566.  Abstract ( 45 )   RICH HTML PDF   Save The regularity of solutions to the Boltzmann equation is a fundamental problem in the kinetic theory. In this paper, the case with angular cut-off is investigated. It is shown that the macroscopic parts of solutions to the Boltzmann equation, i.e., the density, momentum and total energy are continuous functions of (x,t) in the region R3×(0, +∞). More precisely, these macroscopic quantities immediately become continuous in any positive time even though they are initially discontinuous and the discontinuities of solutions propagate only in the microscopic level. It should be noted that such kind of phenomenon can not happen for the compressible Navier-Stokes equations in which the initial discontinuities of the density never vanish in any finite time, see [22]. This hints that the Boltzmann equation has better regularity effect in the macroscopic level than compressible Navier-Stokes equations. References | Related Articles | Metrics

Select

RADIAL SYMMETRY FOR SYSTEMS OF FRACTIONAL LAPLACIAN Congming LI, Zhigang WU Acta Mathematica Scientia. 2018, 38 (5):  1567-1582.  Abstract ( 40 )   RICH HTML PDF   Save In this paper, we consider systems of fractional Laplacian equations in Rn with nonlinear terms satisfying some quite general structural conditions. These systems were categorized critical and subcritical cases. We show that there is no positive solution in the subcritical cases, and we classify all positive solutions ui in the critical cases by using a direct method of moving planes introduced in Chen-Li-Li [11] and some new maximum principles in Li-Wu-Xu [27]. References | Related Articles | Metrics

Select

STRONG COMPARISON PRINCIPLES FOR SOME NONLINEAR DEGENERATE ELLIPTIC EQUATIONS Yanyan LI, Bo WANG Acta Mathematica Scientia. 2018, 38 (5):  1583-1590.  Abstract ( 44 )   RICH HTML PDF   Save In this paper, we obtain the strong comparison principle and Hopf Lemma for locally Lipschitz viscosity solutions to a class of nonlinear degenerate elliptic operators of the form ▽2ψ + L(x, ▽ψ), including the conformal hessian operator. References | Related Articles | Metrics

Select

HÖLDER CONTINUOUS SOLUTIONS OF BOUSSINESQ EQUATIONS Tao TAO, Liqun ZHANG Acta Mathematica Scientia. 2018, 38 (5):  1591-1616.  Abstract ( 31 )   RICH HTML PDF   Save We show the existence of dissipative Hölder continuous solutions of the Boussinesq equations. More precise, for any β ∈ (0, 1/5), a time interval[0, T] and any given smooth energy profile e:[0, T] → (0, ∞), there exist a weak solution (v, θ) of the 3d Boussinesq equations such that (v, θ) ∈ Cβ(T3×[0, T]) with e(t)=∫T3|v(x, t)|2dx for all t ∈[0, T]. This extend the result of [2] about Onsager's conjecture into Boussinesq equation and improve our previous result in [30]. References | Related Articles | Metrics

Select

REVIEW ON MATHEMATICAL ANALYSIS OF SOME TWO-PHASE FLOW MODELS Huanyao WEN, Lei YAO, Changjiang ZHU Acta Mathematica Scientia. 2018, 38 (5):  1617-1636.  Abstract ( 56 )   RICH HTML PDF   Save The two-phase flow models are commonly used in industrial applications, such as nuclear, power, chemical-process, oil-and-gas, cryogenics, bio-medical, micro-technology and so on. This is a survey paper on the study of compressible nonconservative two-fluid model, drift-flux model and viscous liquid-gas two-phase flow model. We give the research developments of these three two-phase flow models, respectively. In the last part, we give some open problems about the above models. References | Related Articles | Metrics