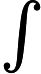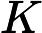[1] Anderson J, Pommerenke C, Clunie J. On Bloch functions and normal functions. J Reine Angew Math, 1974, 270(1): 12-37
[2] Chatzifountas C, Girela D, Peláez J Á. A generalized Hilbert matrix acting on Hardy spaces. J Math Anal Appl, 2014, 413(1): 154-168
[3] Carleson L. Interpolations by bounded analytic functions and the corona problem. Ann of Math, 1962, 76(3): 547-559
[4] Cowen C C, MacCluer B D. Composition Operators on Spaces of Analytic Functions. Boca Raton: CRC Press, 1995
[5] Cwikel M, Kalton N J. Interpolation of compact operators by the methods of Calderón and Gustavsson-Peetre. Proc Edinburgh Math Soc, 1995, 38(2): 261-276
[6] Deng F, Ouyan C, Deng G. Some questions regarding verification of Carleson measure. Acta Math Sci, 2021, 41B(6): 2136-2148
[7] Diamantopoulos E, Siskakis A G. Composition operators and the Hilbert matrix. Studia Math, 2000, 140(2): 191-198
[8] Duren P L. Extension of a theorem of Carleson. Bull Amer Math Soc, 1969, 75: 143-146
[9] Duren P L.Theory of   Spaces. New York: Academic Press, 1970 Spaces. New York: Academic Press, 1970
[10] Duren P L, Romberg B W, Shields A L. Linear functionals on   spaces with spaces with      . Reine Angew Math, 1969, 238(1): 32-60 . Reine Angew Math, 1969, 238(1): 32-60
[11] Galanopoulos P, Girela D, Peláez J Á, Siskakis A G. Generalized Hilbert operators. Ann Acad Sci Fenn Math, 2014, 39: 231-258
[12] Galanopoulos P, Peláez J Á. A Hankel matrix acting on Hardy and Bergman spaces. Studia Math, 2010, 200(3): 201-220
[13] Girela D.Analytic functions of bounded mean oscillation//Complex Function Spaces, University Joensuu Dept Math Rep Ser, vol 4. Joensuu: University Joensuu, 2001: 61-170
[14] Girela D, Merchán N. A generalized Hilbert operator acting on conformally invariant spaces. Banach J Math Anal, 2016, 12(2): 374-398
[15] Gnuschke-Hauschild D, Pommerenke C. On Bloch functions and gap series. J Reine Angew Math, 1986, 367: 172-186
[16] Li S, Zhou J. Essential norm of generalized Hilbert matrix from Bloch type spaces to BMOA and Bloch space. AIMS Math, 2021, 6: 3305-3318
[17] Maccluer B, Zhao R. Vanishing logarithmic Carleson measures. Illinois J Math, 2002, 46(2): 507-518
[18] Ye S, Zhou Z. A derivative-Hilbert operator acting on the Bloch space. Complex Anal Oper Theory, 2021, 15(5): 88
[19] Ye S, Zhou Z. A derivative-Hilbert operator acting on Bergman spaces. J Math Anal Appl, 2022, 506(1): 125553
[20] Zhao R. On logarithmic Carleson measures. Acta Sci Math, 2003, 69: 605-618
[21] Zhu K. Bloch type spaces of analytic functions. Rocky Mountain J Math, 1993, 23(3): 1143-1177
[22] Zhu K.Operator Theory in Function Spaces. Surveys Monoge 138. 2nd ed. Providence RI: Amer Math Soc, 2007 |