数学物理学报(英文版) ›› 2023, Vol. 43 ›› Issue (1): 156-168.doi: 10.1007/s10473-023-0110-y
BOUNDEDNESS OF A CHEMOTAXIS-CONVECTION MODEL DESCRIBING TUMOR-INDUCED ANGIOGENESIS*
Haiyang Jin†, Kaiying Xu
- School of Mathematics, South China University of Technology, Guangzhou 510640, China
-
收稿日期:2021-08-05修回日期:2022-07-07发布日期:2023-03-01 -
通讯作者:†Haiyang JIN.E-mail: mahyjin@scut.edu.cn -
基金资助:*NSF of China (11871226), Guangdong Basic and Applied Basic Research Foundation (2020A1515010140 and 2022B1515020032), Guangzhou Science and Technology Program (202002030363).
BOUNDEDNESS OF A CHEMOTAXIS-CONVECTION MODEL DESCRIBING TUMOR-INDUCED ANGIOGENESIS*
Haiyang Jin†, Kaiying Xu
- School of Mathematics, South China University of Technology, Guangzhou 510640, China
-
Received:2021-08-05Revised:2022-07-07Published:2023-03-01 -
Contact:†Haiyang JIN.E-mail: mahyjin@scut.edu.cn -
About author:Kaiying Xu, E-mail: 201920127920@mail.scut.edu.cn -
Supported by:*NSF of China (11871226), Guangdong Basic and Applied Basic Research Foundation (2020A1515010140 and 2022B1515020032), Guangzhou Science and Technology Program (202002030363).
摘要: This paper is concerned with the parabolic-parabolic-elliptic system 













































































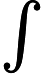



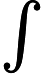








































































































引用本文
Haiyang Jin, Kaiying Xu. BOUNDEDNESS OF A CHEMOTAXIS-CONVECTION MODEL DESCRIBING TUMOR-INDUCED ANGIOGENESIS*[J]. 数学物理学报(英文版), 2023, 43(1): 156-168.
Haiyang Jin, Kaiying Xu. BOUNDEDNESS OF A CHEMOTAXIS-CONVECTION MODEL DESCRIBING TUMOR-INDUCED ANGIOGENESIS*[J]. Acta mathematica scientia,Series B, 2023, 43(1): 156-168.
使用本文
| [1] Bourguignon J P, Brezis H.Remarks on Euler equation. J Funct Anal, 1974, 15: 341-363 [2] Bellomo N, Bellouquid A, Tao Y S, et al.Toward a mathematical theory of Keller-Segel models of pattern formation in biological tissues. Math Models Methods Appl Sci, 2015, 25(9): 1663-1763 [3] Cao X.Global bounded solutions of the higher-dimensional Keller-Segel system under smallness conditions in optimal spaces. Discrete Contin Dyn Syst, 2015, 35: 1891-1904 [4] Chu J W, Jin H Y, Xiang T.Global dynamics in a chemotaxis model describing tumor angiogenesis with/without mitosis in any dimensions. arXiv:2106.11525, 2021 [5] Espejo E, Suzuki T.Global existence and blow-up for a system describing the aggregation of microglia. Appl Math Lett, 2014, 35: 29-34 [6] Horstmann D.From 1970 until present: The Keller-Segel model in chemotaxis and its consequences. I. Jahresber Deutsch Math-Verien, 2003, 105(3): 103-165 [7] Horstmann D, Wang G F.Blow-up in a chemotaxis model without symmetry assumptions. Eur J Appl Math, 2001, 12(2): 159-177 [8] Ishida S, Seki K, Yokota T.Boundedness in quasilinear Keller-Segel systems of parabolic-parabolic type on non-convex bounded domains. J Differential Equations, 2014, 256(8): 2993-3010 [9] Jäger W, Luckhaus S.On explosions of solutions to a system of partial differentail equations modelling chemotaxis. Trans Amer Math Soc, 1992, 329: 819-824 [10] Jin H Y.Boundedness of the attraction-repulsion Keller-Segel system. J Math Anal Appl, 2015, 422: 1463-1478 [11] Jin H Y, Wang Z A.Boundedness, blowup and critical mass phenomenon in competing chemotaxis. J Differential Equations, 2016, 260: 162-196 [12] Jin H Y,Wang Z A.Global stabilization of the full attraction-repulsion Keller-Segel system. Discrete Contin Dyn Syst, 2020, 40: 3509-3527 [13] Jin H Y, Xu J.Analysis of the role of convection in a system describing the tumor-induced angiogenesis. Comm Math Sci, 2021, 19(4): 1033-1049 [14] Li Y, Li Y X.Blow-up of nonradial solutions to attraction-repulsion chemotaxis system in two dimensions. Nonlinear Anal Real Word Appl, 2016, 30: 170-183 [15] Li G, Tao Y S.Analysis of a chemotaxis-convection model of capillary-sprout growth during tumor angiogenesis. J Math Anal Appl, 2020, 481: 123474 [16] Lin K, Mu C, Wang L.Large-time behavior of an attraction-repulsion chemotaxis system. J Math Anal Appl, 2015, 426: 105-124 [17] Lin K, Mu C, Zhou D.Stabilization in a higher-dimensional attraction-repulsion chemotaxis system if repulsion dominates over attraction. Math Models Methods Appl Sci, 2018, 28: 1105-1134 [18] Liu D, Tao Y S.Global boundedness in a fully parabolic attraction-repulsion chemotaxis model. Math Methods Appl Sci, 2015, 38: 2537-2546 [19] Mizoguchi N, Souplet P.Nondegeneracy of blow-up points for the parabolic Keller-Segel system. Ann Inst H Poincaré Anal Non Linéaire, 2014, 31(4): 851-875 [20] Luca M, Chavez-Ross A, Edelstein-Keshet L, et al.Chemotactic signaling, Microglia, and alzheimer’s disease senile plagues: Is there a connection? Bull Math Biol, 2003, 65: 693-730 [21] Nagai T, Senba T, Yoshida K.Application of the Trudinger-Moser inequality to a parabolic system of chemotaxis. Funkcial Ekvac Ser Internat, 1997, 40(3): 411-433 [22] Orme M E, Chaplain M A J. A mathematical model of the first steps of tumour-related angiogenesis: Capillary sprout formation and secondary branching. IMA J Math Appl Med Biol, 1996, 13(2): 73-98 [23] Souplet P, Quittner P.Superlinear Parabolic Problems: Blow-up, Global Existence and Steady States. Birkhäuser Advanced Texts. Basel/Boston/Berlin: Birkhäuser, 2007 [24] Tao Y S, Wang Z A.Competing effects of attraction vs. repulsion in chemotaxis. Math Models Methods Appl Sci, 2013, 23: 1-36 [25] Tao Y, Winkler M.The dampening role of large repulsive convection in a chemotaxis system modeling tumor angiogenesis. Nonlinear Anal, 2021, 208: 112324 [26] Winkler M.Aggregation vs. global diffusive behavior in the higher-dimensional Keller-Segel model. J Differential Equations, 2010, 248(12): 2889-2905 [27] Winkler M.Boundedness in the higher-dimensional parabolic-parabolic chemotaxis system with logistic source. Comm Part Differ Eq, 2010, 35(8): 1516-1537 [28] Winkler M.Finite-time blow-up in the higher-dimensional parabolic-parabolic Keller-Segel system. J Math Pures Appl, 2013, 100(5): 748-767 |
| Viewed | ||||||||||||||||||||||||||||||||||||||||||||||
|
Full text 7
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Abstract 83
|
|
|||||||||||||||||||||||||||||||||||||||||||||
Cited |
|
|||||||||||||||||||||||||||||||||||||||||||||
| Shared | ||||||||||||||||||||||||||||||||||||||||||||||
| Discussed | ||||||||||||||||||||||||||||||||||||||||||||||