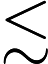数学物理学报(英文版) ›› 2010, Vol. 30 ›› Issue (6): 2103-2109.doi: 10.1016/S0252-9602(10)60194-4
SMOOTHING ESTIMATES OF THE RADIAL SCHRÖDINGER PROPAGATOR IN DIMENSIONS n≥2
李栋, 张晓轶
- Department of Mathematics, University of Iowa, 14 MacLean Hall, Iowa City, 52242, USA|
Department of Mathematics, University of Iowa, 14 MacLean Hall, Iowa City, 52242, USA Academy of Mathematics and System Sciences, Chinese Academy of Sciences, Beijing 100190, China
SMOOTHING ESTIMATES OF THE RADIAL SCHRÖDINGER PROPAGATOR IN DIMENSIONS n≥2
LI Dong, ZHANG Xiao-Tie
- Department of Mathematics, University of Iowa, 14 MacLean Hall, Iowa City, 52242, USA|
Department of Mathematics, University of Iowa, 14 MacLean Hall, Iowa City, 52242, USA Academy of Mathematics and System Sciences, Chinese Academy of Sciences, Beijing 100190, China
摘要:
The usual Kato smoothing estimate for the Schr\"odinger propagator in 1D takes the form . In dimensions the smoothing estimate involves certain localization to cubes in space. In this paper we focus on radial functions and obtain Kato-type sharp smoothing estimates which can be viewed as natural eneralizations of the 1D Kato smoothing. These estimates are global in the sense that they do not need localization in space. We also
present an interesting counterexample which shows that even though the time-global inhomogeneous Kato smoothing holds true, the corresponding time-local inhomogeneous smoothing estimate cannot hold in general.
中图分类号:
- 35Q55