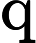数学物理学报(英文版) ›› 2010, Vol. 30 ›› Issue (5): 1577-1592.doi: 10.1016/S0252-9602(10)60151-8
POSITIVE SOLUTIONS FOR WEAKLY COUPLED NONLINEAR ELLIPTIC SYSTEMS
龙静, 杨健夫
- Wuhan Institute of Physics and Mathematics, Chinese Academy of Sciences, |Wuhan 430071, China
Graduate School, Chinese Academy of Sciences, Beijing 100049, China; Department of Mathematics, Jiangxi Normal University, Nanchang 330022, China
POSITIVE SOLUTIONS FOR WEAKLY COUPLED NONLINEAR ELLIPTIC SYSTEMS
LONG Jing, YANG Jian-Fu
摘要:
In this article, we consider the existence of positive solutions for weakly coupled nonlinear elliptic systems
To find nontrivial solutions, we first investigate autonomous systems. In this case, results of bifurcation from semi-trivial solutions are obtained by the implicit function theorem. Next, the existence of positive solutions of problem (0.1) is obtained by variational methods.
中图分类号:
- 35J50